[Deep Learning Specialization - 2단계] 7. 다중 클래스 분류

Softmax 회귀

우리는 지금까지 두 가지 클래스에 따른 분류만을 살펴보았다. 사진이 고양이인가, 아닌가와 같은 사례처럼 말이다. 그러나 Softmax 회귀를 이용하면 여러 개의 클래스에 대해서도 분류를 할 수 있다.

C를 클래스의 개수라고 하자. 아래 그림은 C가 4일 때의 상황을 나타낸 것이다.

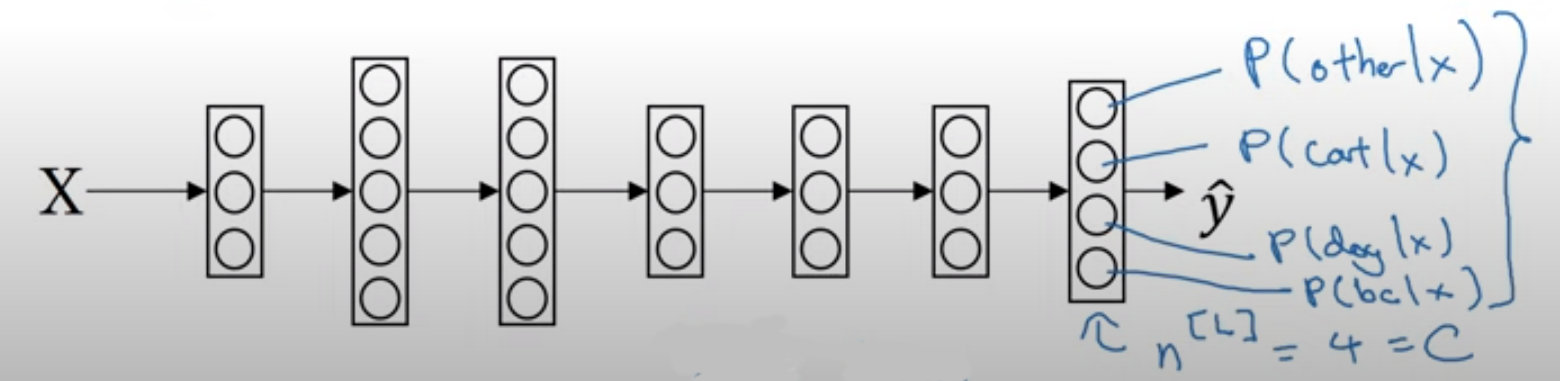
마지막 층에 주목하자. $\hat{y}$는 더 이상 어떤 실수가 아니다. Softmax 회귀에서는 벡터로 표현된다. 여기서는 C가 4이기 때문에, (4, 1)의 벡터로 표현되었다. 벡터 각각의 요소는 4개의 클래스 각각에 해당될 조건부 확률을 나타낸다. 예를 들자면 ‘입력값 x가 주어졌을 때 병아리일 확률’처럼 말이다.

계산하는 방법도 알아보자. 먼저 보통의 신경망에서처럼 Z를 계산한다.

\[Z^{L} = W^{L}a^{[L-1]} + b^{[L]}\]

이 다음부터가 Softmax 회귀의 가장 큰 특징이라 할 수 있다. t라는 임시변수를 사용하여 다음과 같이 계산한다.

\[t = e^{Z^{[L]}}\] \[a^{[L]} = \frac{e^{Z^{[L]}}}{\displaystyle \sum_{j=1}^{C}{t_i}},\quad a_i^{[L]} = \frac{t_i}{\displaystyle \sum_{j=1}^{C}{t_i}}\]

위 식에서 t, a는 모두 (C, 1)의 벡터이다. 위 과정을 직관적으로 이해하면, 각 클래스의 확률을 구해 모두 더하고, 이렇게 구한 합을 이용해 확률의 총합이 1이 되도록 각각의 확률을 재조정해주는 것이다.

C가 4일 때의 예시를 하나 살펴보자. $Z^{[L]}$가 다음과 같다고 해보자.

\[Z^{[L]} = \begin{bmatrix} 5\\2\\-1\\3 \end{bmatrix}\]

그럼 t는 다음과 같이 구한다.

\[t = \begin{bmatrix} e^5\\ e^2 \\ e^{-1}\\ e^3 \end{bmatrix} = \begin{bmatrix} 148.4\\ 7.4 \\ 0.4\\ 20.1 \end{bmatrix}\]

t 각각의 요소($t_j$)를 모두 합한 값은 176.3이다. $a^{[L]}$는 아래와 같다.

\[a^{[L]} = \frac{t}{176.3}\]

첫 번째 클래스일 확률은 $\frac{e^5}{176.3}$, 두 번째 클래스일 확률은 $\frac{e^2}{176.3}$ 이런 식으로 되는 것이다.

Softmax 회귀 과정을 요약하면 다음 식과 같다.

\[a^{[L]} = g^{[L]}(Z^{[L]})\]

특이한 것은, 활성 함수에 넣어도 벡터 상태를 그대로 유지한다는 점이다. Softmax 회귀에서는 입력과 출력이 모두 벡터이다.

은닉층이 없는 Softmax 회귀는 선형적인 기준을 가진다. 그러나 은닉층이 많아지고 신경망이 복잡해지면 비선형적인 분류 함수들도 볼 수 있다.

cf. Softmax라는 이름은 ‘부드러운 성질’을 가졌기 때문에 붙여졌다. 모든 클래스에 대한 확률을 살려주기 때문이다. Softmax와 반대되는 Hardmax는 가장 높은 확률을 가진 클래스의 확률을 1로 바꾸고, 그외에는 모두 확률이 0이 되도록 한다.

Softmax 회귀는 두 클래스만 다루는 로지스틱 회귀를 일반화한 것으로 볼 수 있다. Softmax 회귀에서 C = 2일 때를 로지스틱 회귀 상황으로 볼 수 있다. 로지스틱 회귀에서는 하나의 값만을 구하지 않느냐고 되물을 수 있다. 이에 대한 증명은 간단한데, 확률의 총합은 1이어야 하므로, C가 2일 때는 굳이 두 클래스의 확률을 모두 구할 필요가 없다.

Softmax 훈련시키기

Softmax에서의 손실함수와 비용함수를 살펴보자. 식은 다음과 같다.

\[L(\hat{y}, \, y) = -\displaystyle \sum_{j=1}^{C}{y_j \log{\hat{y_j}}}\] \[J(w, \, b) = \frac{1}{m}\displaystyle \sum_{i=1}^{m}{L(\hat{y}^{(i)}, \, y^{(i)})}\]

예시를 통해 더 직관적으로 이해해보자.

\[y = \begin{bmatrix} 0\\1\\0\\0 \end{bmatrix}, \quad a^{[L]}= \hat{y} = \begin{bmatrix} 0.3\\0.2\\0.1\\0.4 \end{bmatrix}\]

정답인 $y$와 신경망을 통해 구한 $\hat{y}$는 다소 차이가 있어 보인다. $y_2$가 1인 것에 비해, $\hat{y}_2$는 그 확률이 0.2밖에 되지 않기 때문이다. 손실함수에 넣고 계산해보자.

\[L(\hat{y}, \, y) = -\displaystyle \sum_{j=1}^{4}{y_j \log{\hat{y_j}}}\\ = -y_2 \log{\hat{y}_2} \\= -\log{\hat{y}_2}\]

우리는 손실함수를 최소화하고 싶다. 즉, $\hat{y}_2$를 최대한 크게 해야하는 것이다.

참고로, 구현할 때는 $y^{(m)}$과 $\hat{y}^{(m)}$들을 나란히 쌓아서 행렬 $Y$와 $\hat{Y}$를 만든다.

마지막으로 경사하강법을 구현해보자. 신경망의 마지막 층에서 역방향 전파는 $dz^{[L]} = \hat{y} - y$이다. 해당 식에 등장하는 모든 요소는 크기가 (C, 1)인 벡터이다.

역방향전파 더 알아보기

실제로 Softmax를 구현할 때는 정방향 전파만을 잘 고려해주면 된다. 정방향 전파의 방식을 정해주면, 딥러닝 프레임워크가 알아서 역방향 전파를 할 것이다.

모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.