모멘텀 최적화 알고리즘
경사하강법의 진행 과정을 그림으로 나타내면 다음과 같다.
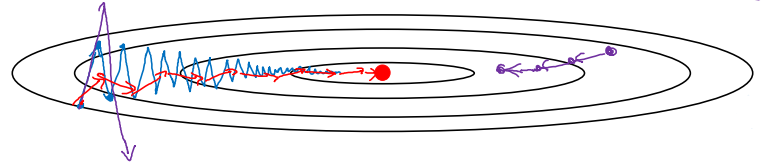
우리는 여기서 상하의 학습률은 줄이고, 좌우의 학습률을 늘리고 싶다. 상하의 학습률을 줄여야 진동이 커지는 것을 막을 수 있으며, 좌우의 학습률을 늘려야 최적 값까지 빠르게 이동할 것이기 때문이다.
모멘텀을 이용한 경사하강법은 다음과 같이 구현한다.
On iteration t:
Compute dW, db on current mini-batch
V_dW = beta * V_dW + (1 - beta) * dW # 지수가중평균 참고
V_db = beta * V_db + (1 - beta) * db
W = W - alpha * V_dW, b = b - alpha * V_db
코드가 알아보기 힘들어 중간 과정을 다시 써봤다.
$V_{dW} = \beta \cdot V_{dW} + (1 - \beta) \cdot dW$
$V_{db} = \beta \cdot V_{db} + (1 - \beta) \cdot db$
이와 같이 지수가중평균을 적용해주면 경사 하강 정도가 부드러워질 것이다. 수직(상하) 방향의 평균은 양수와 음수의 평균이기 때문에 0에 가까워지는 한편, 수평(좌우)의 평균은 0보다 큰 값들이기 때문에 상당히 큰 값을 가질 것이다. 결국 우리가 원하는 것처럼 수직방향의 진동은 줄어들고, 수평 방향의 폭은 증가하는 효과가 생긴다.
물리적인 직관으로도 이해가 가능하다. 밥그릇과 같이 생긴 함수 위에서 경사하강법을 시행한다고 생각해보자. dW, db는 아래로 하강할 때의 가속, $V_{dW}$, $V_{db}$는 하강 속도를 의미한다. 그리고 계수 $\beta$는 마찰을 의미할 것이다.
여기서 $\alpha$와 $\beta$는 초매개변수이다. 보통 $\beta$는 0.9의 값을 가진다.
가끔 $V_{dW} = \beta \cdot V_{dW} + dW$와 같이 뒤쪽의 $(1 - \beta)$가 생략된 경우가 있다. 이는 $\frac{1}{(1 - \beta)}$로 스케일링이 된 것이다. 그러나 이렇게 하면 학습률 수정 등에서 추가 단계가 필요하기 때문에 비효율적이게 된다.
RMSprop
앞선 상황과 동일하게 우리는 수직 방향의 진동은 최소화하고, 수평 방향의 진행은 빠르게 하고 싶다. RMSprop는 이를 가능하게 하는 또 다른 알고리즘이다.
RMSprop는 앞서 살펴본 모멘텀 경사하강법의 코드에서 Compute이후의 과정을 다음과 같이 바꾸면 된다. 여기서 b는 수직방향, W는 수평방향이라고 가정한다.
$S_{dW} = \beta_2 S_{dW} + (1 - \beta_2) dW^2$
$S_{db} = \beta_2 S_{db} + (1 - \beta_2) db^2$
$W = W - \alpha \frac{dW}{\sqrt{S_{dW} + \epsilon}}, \, b = b - \alpha \frac{db}{\sqrt{S_{db} + \epsilon}}$
$\epsilon$은 보통 $10^{-8}$정도의 값을 사용한다.
식을 이해해보자. 제곱으로 작성한 부분은 사실 요소별 곱셈(element-wise)이다. dW는 작은 값이기 때문에, 제곱을 해도 더 작아진다. 반대로 db는 큰 값이기 때문에 제곱을 하면 더 커진다. 마지막 식에서, 미분 값이 큰 경우에는 더 큰 값으로 나눗셈을 하게 되고, 미분 값이 작은 곳에서는 더 작은 값으로 나눗셈을 하게 된다(큰 값은 많이 줄이고 작은 값은 적게 줄인다고 이해하면 쉽다). 즉, 수직 방향의 진동을 줄이고 수평 방향의 진행을 빠르게 하는 효과가 있는 것이다.
RMSprop를 적용한 경사하강법은 다음 그림의 녹색 화살표처럼 된다.

Adam 최적화 알고리즘
Adam(Adaptive Moment estimation) 최적화 알고리즘에서는 모멘텀과 RMSprop를 섞는다. 초반에 $V_{dW}$, $S_{dW}$, $V_{db}$, $S_{db}$를 모두 0으로 초기화한 뒤, Compute이후의 과정을 다음과 같이 만든다.
$V_{dW} = \beta_1 V_{dW} + (1 - \beta_1) dW,\, V_{db} = \beta_1 V_{db} + (1 - \beta_1) db$
$S_{dW} = \beta_2 S_{dW} + (1 - \beta_2) dW^2, \, S_{db} = \beta_2 S_{db} + (1 - \beta_2) db^2$
$V^{corrected}{dW} = \frac{V{dW}}{(1-\beta_1^t)}, \, V^{corrected}{db} = \frac{V{db}}{(1-\beta_1^t)}$
$S^{corrected}{dW} = \frac{S{dW}}{(1-\beta_2^t)}, \, S^{corrected}{db} = \frac{S{db}}{(1-\beta_2^t)}$
$W = W - \alpha \frac{V^{corrected}{dW}}{\sqrt{S^{corrected}{dW}} + \epsilon}, \, b = b - \alpha \frac{V^{corrected}{db}}{\sqrt{S^{corrected}{db}} + \epsilon}$
매우 많은 초매개변수가 등장한다. $\alpha$는 학습률로, 많은 조정이 필요한 값이다. $\epsilon$은 $10^{-8}$을 주로 사용한다. $\beta_1$은 0.9를, $\beta_2$는 0.999를 주로 사용한다.
학습률 감쇠
매우 큰, 고정된 학습률은 학습의 초반에는 좋은 성능을 보일지 몰라도 최적화 값에 가까워지면 최적화 값에 근접하지 못하고 주위를 맴도는 현상이 발생할 수 있다. 아래 그림의 파란색 선처럼 말이다.
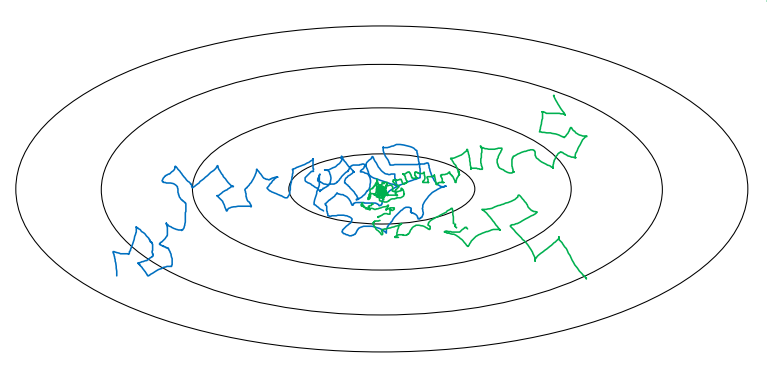
이를 위해서는 초반에는 큰 학습률을 사용하고, 점차 학습률을 감소시키는 방식을 사용해야 한다. 학습률 감쇠는 다음과 같이 감쇠 속도(r)와 epoch 수(n)에 대한 공식으로 나타낼 수 있다.
\[\alpha = \frac{1}{1 + r \times n} \alpha_0\]Epoch가 증가할수록 학습률이 감소할 것이다. 즉, 초록색 선처럼 최적 값에 매우 근접할 수 있다.
학습률을 줄이는 다른 방법들도 있다.
$\alpha = 0.95^{n}\alpha_0$
$\alpha = \frac{k}{\sqrt{n}}\alpha_0$
또한, 단계별로 학습률을 다르게 설정하거나 일일이 직접 학습률을 조정해주는 방법도 있다.
지역 최적값의 문제
다른 강의에서도 살펴보았듯이, 경사하강법에서는 지역 최적값에 머물러 전역 최적으로 이동하지 못하는 문제가 발생할 수 있다. 아래와 같은 그림을 흔히 생각해볼 수 있다.
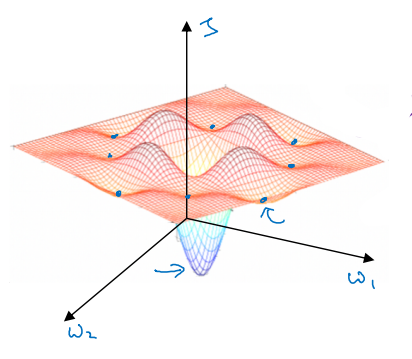
그러나 차원이 커질 경우 지역 최적의 문제는 생각보다 심각하지 않다. 오히려 문제가 되는 것은 안장점에 관한 것이다. 지역 최적값이 밥그릇 모양인 것과 다르게, 안장점에서는 모든 방향에서 아래로 볼록하지 않다. 모든 방향에서 아래로 볼록할 확률보다 그렇지 않을 확률이 압도적을 높기에, 안장점은 지역 최적값보다 더 흔하게 나타난다.
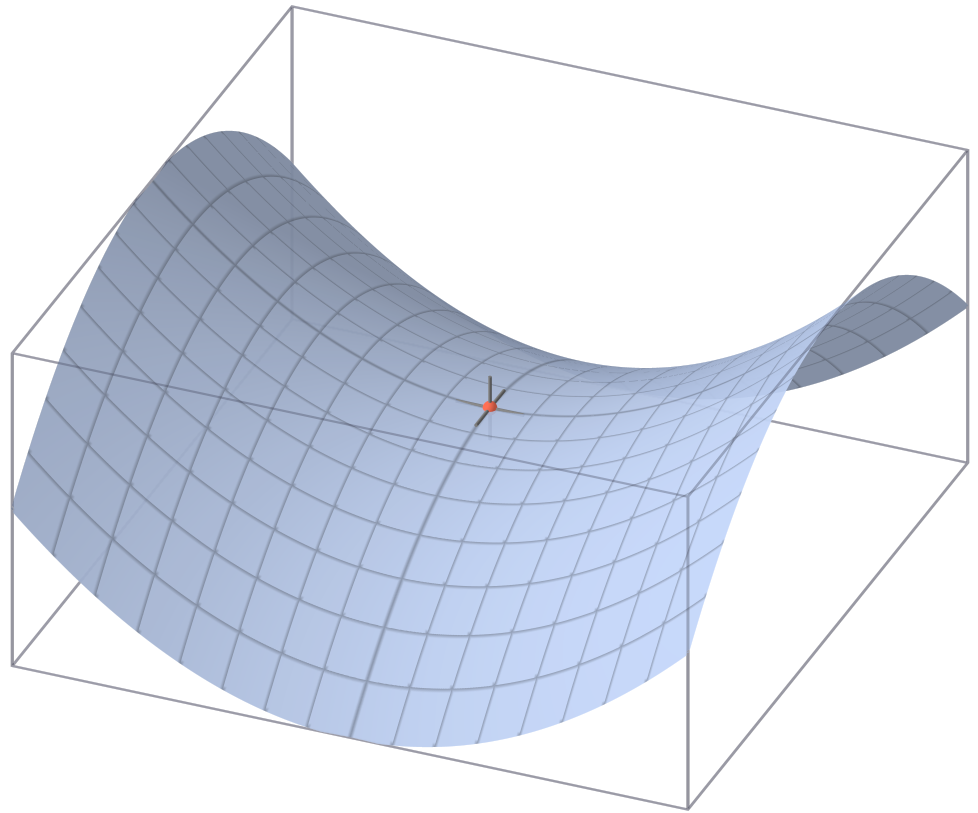
안장점으로 향하는 구간인 안장지대에서는 기울기가 아주 오랫동안 0에 가깝게 유지된다. 이는 학습을 매우 느리게 하며, 안장점을 벗어나서 경사하강법이 다시 속개되는 것에 상당한 방해가 된다.

다행히도, RMSprop이나 Adam 최적화 알고리즘은 안장지대의 문제를 해결하는 데 도움을 준다.
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기