선형 회귀 개요
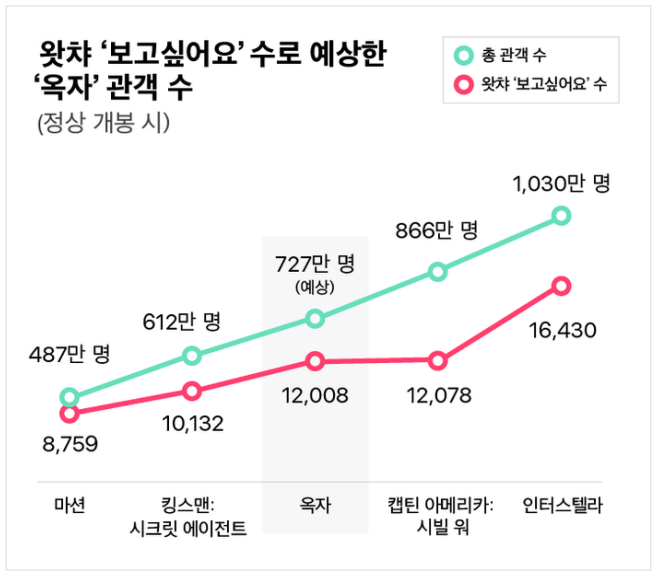
앞선 강의에서 영화 ‘옥자’의 관객 수를 예측했던 과정이 바로 선형 회귀이다. 사전적 정의는 ‘종속 변수 y와 한 개 이상의 독립 변수 X와의 선형 상관 관계를 모델링하는 회귀분석 기법’이다 (출처: 위키백과).
선형 회귀에서는 예측 함수와 실제 값의 오차를 최대한 줄여야 한다. 그냥 오차를 더하면 양수와 음수가 섞여 상쇄될 수도 있으므로 오차의 제곱을 더해준다.
영화 ‘옥자’의 관객 수를 예측하는 과정을 다시 보자. 매개 변수가 $w_1$, $w_2$ 라고 할 때, 예측 값 $\hat{y}$ 은 다음과 같다.
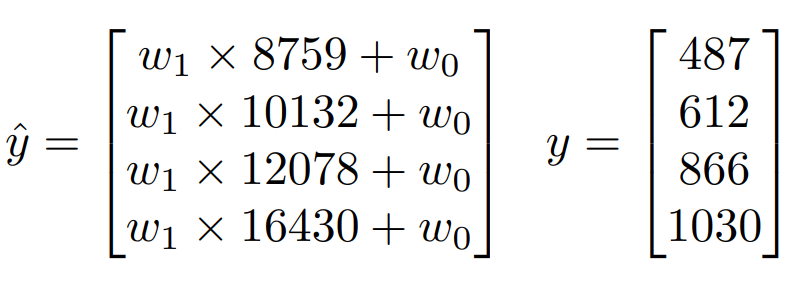
오차의 제곱은 다음과 같다.
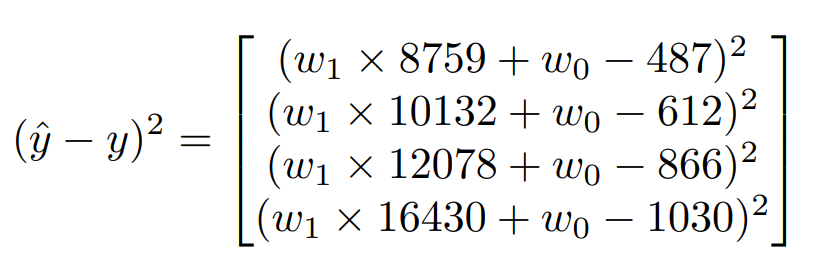
우리의 목표는 오차의 합을 최소화하는 $w_1$, $w_2$ 를 구하는 것이다. 그리고 이 과정에는 미분을 사용하면 된다.
비용 함수
오차 제곱의 합(혹은 이를 평균한 식)을 비용 함수라고 한다. $h_{\theta}(x)$ 를 가설 함수(예측 함수)라고 하면 비용 함수는 다음과 같이 정의된다.
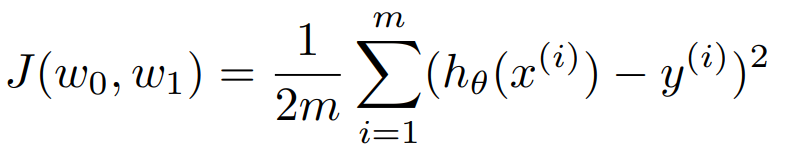
예측 값과 실제 값의 차이를 제곱한 뒤, 이를 모두 더했다(데이터의 개수가 m). 그냥 오차의 제곱만 모두 더하면 수가 매우 커질 수 있으므로 m으로 나누어서 평균을 냈다. 숫자 2는 미분을 대비한 것이다.
비용 함수 식에서 궁금한 것은 비용 함수를 최소화하는 $\theta$를 구하는 것이다.
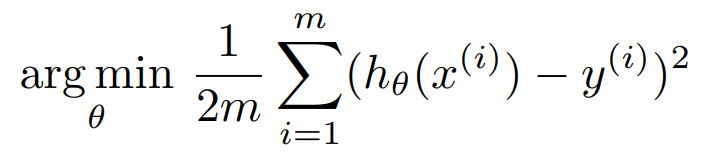
앞서 최소화하는 매개변수를 구할 때는 미분을 한다고 했다. $w_1$, $w_2$ 에 대해 각각 편미분을 하면 다음과 같다.
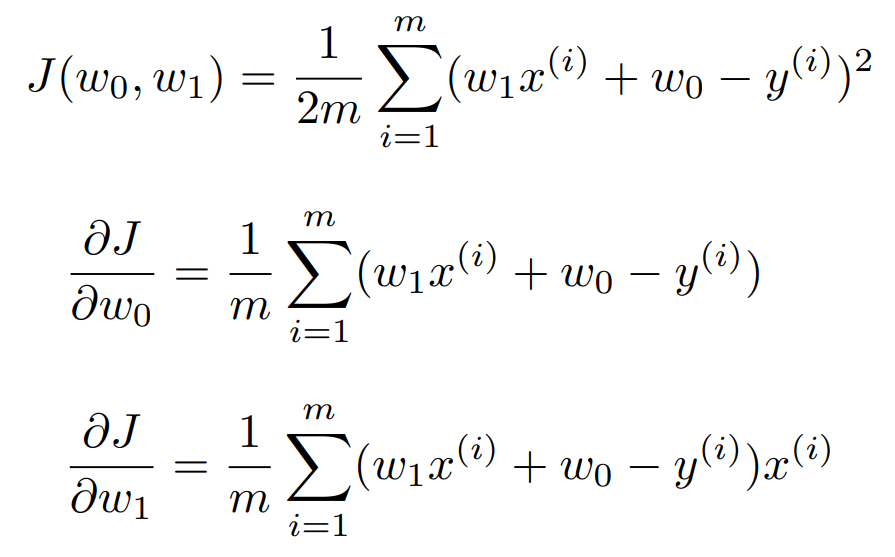
이 결과를 이용해 최적 값을 찾는 방법에는 정규 방정식(normal equation)과 경사 하강법(gradient descent)이 있다.

딥러닝에서 많이 사용하는 미분 방법들이다. 특히 마지막의 연쇄 법칙을 눈여겨 보자.
정규 방정식
정규 방정식을 먼저 알아보자. 일단 y, X, w를 다음과 같이 쓸 수 있다.
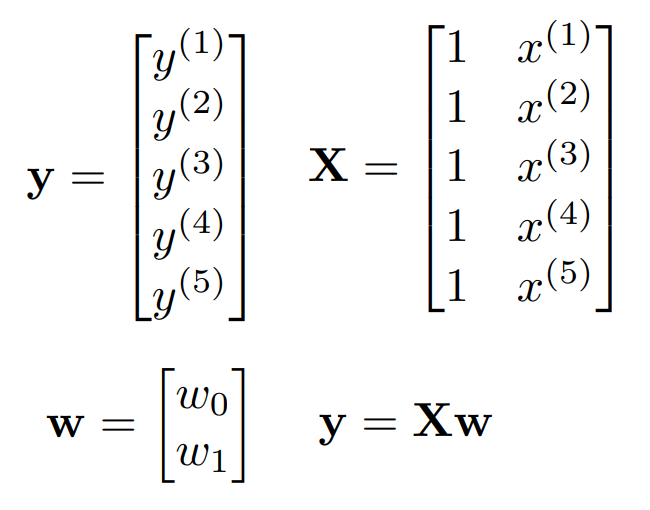
행렬 X에서 1은 상수항을 나타낸다. 이들의 관계는 $y=Xw$ 이다.
앞서 비용 함수를 편미분한 식들을 살펴보았다. 그 식들을 0으로 만드는 값을 알고 싶으므로 다음과 같이 놓는다.
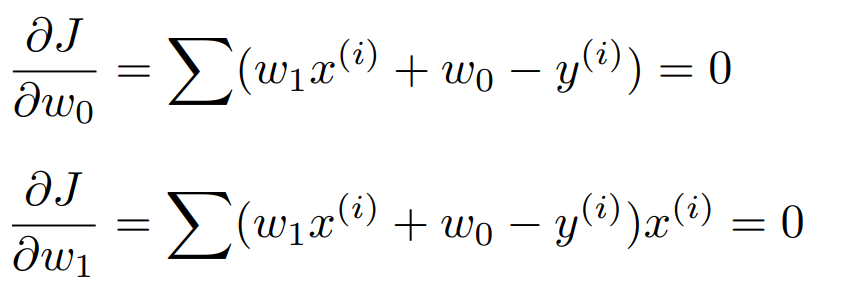
이 식을 정리하면 다음과 같다.
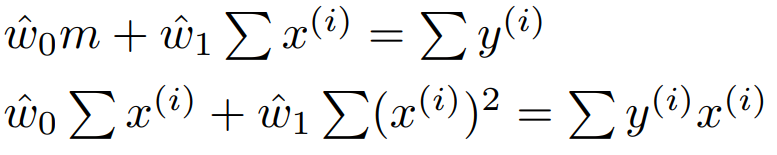
위 식의 좌측 변을 행렬로 나타낸다면 $X^{T}X \hat{w}$ 가 된다.
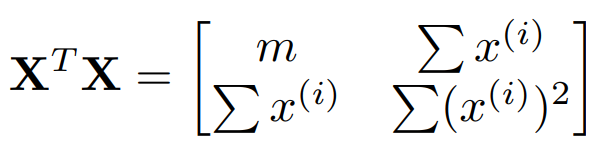
또한 우변은 $X^{T}y$ 가 된다. 따라서 $\hat{w}$ 은 다음과 같이 구할 수 있다.
\[\hat{w} = (X^{T}X)^{-1}X^{T}y\]$X^{T}X$ 의 역행렬을 구하기 위해 $det(X^{T}X)$ 를 구하면 다음과 같다.
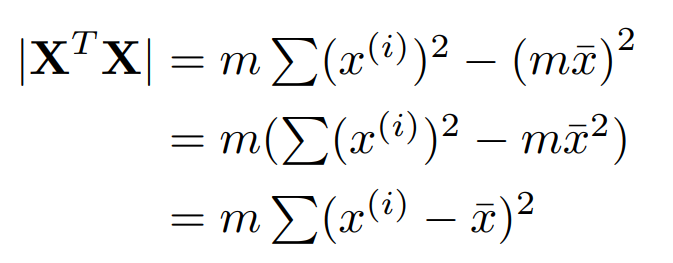
변량이 도출된다! 역행렬 자체는 다음과 같다.
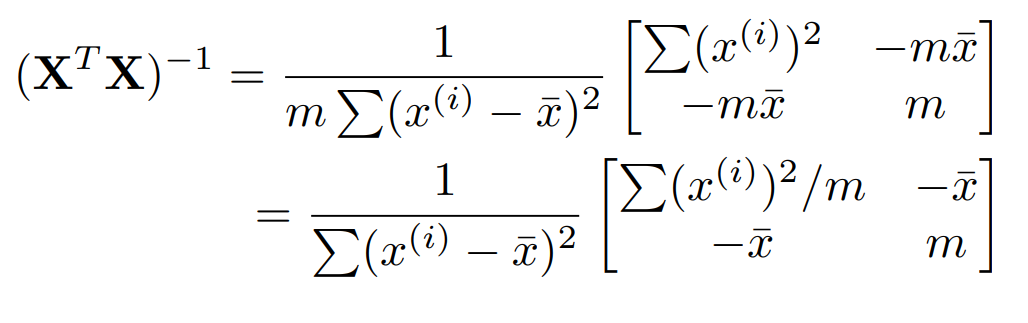
이제 $(X^{T}X)^{-1}X^{T}y$ 를 구해보자.
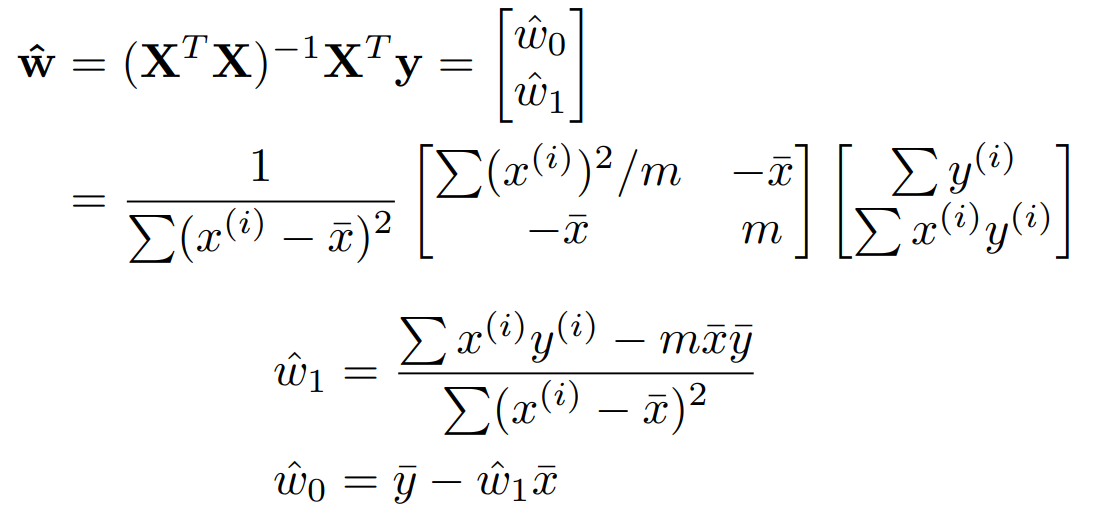
여기서는 매개변수가 2개였지만 더 많은 경우가 있을 수 있다. 그 때는 $X^{T}X$ 가 아래와 옆으로 확대된다.
보통 선형 회귀하면 ‘경사 하강법’을 떠올리지만 실제로는 정규 방정식도 많이 사용한다. 대부분의 경우 $X^{T}X$ 가 존재하고, 사용자가 직접 지정해야하는 초매개변수가 없기 때문이다. 다만, 특성이 많으면 계산이 좀 느려질 수는 있다.
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기