딕셔너리
파이썬에서 해싱(hashing)은 딕셔너리로 구현되어 있다. 딕셔너리는 추상 자료형으로 다음과 같은 작업을 수행할 수 있다.
| 작업 | 의미 |
|---|---|
| insert(item) | 집합에 항목 추가. 이미 있는 경우는 덮어쓰기. |
| delete(item) | 집합에서 항목 제거 |
| search(key) | 존재할 경우 키와 항목 반환 |
항목은 각자의 키를 가지고 있으며, 키는 겹치면 안된다.
딕셔너리에서 연산은 하나당 상수의 시간($O(n)$)을 가진다.
딕셔너리의 중요성
딕셔너리는 다음과 같은 이유에서 중요하다.
- 현대 프로그래밍 언어에 다 내장되어 있다.
- 문서 거리 문제 등에 활용된다.
- 데이터베이스 구현에 사용된다. (ex. 맞춤법 교정 프로그램, 로그인 프로그램)
- 컴파일러와 인터프리터에 사용된다.
- 네트워크 구현에 사용된다.
그 외에도 부분 문자열 탐색, 암호학 등에도 간접적으로 사용된다.
프리해시와 해싱
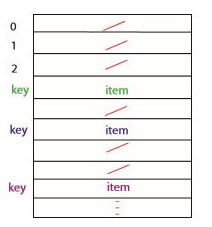
위와 같은 직접 접근 테이블이 있다고 해보자. 키가 음이 아닌 수이고, 빈 공간에 null이 저장된다면 다음과 같은 문제가 발생할 수 있다.
- 키가 정수가 아닐 수 있다.
- null까지 저장하기 위한 큰 메모리 공간이 필요하다.
1번 문제를 먼저 해결하자. 이를 위해서는 ‘프리해시(prehash)’를 사용한다. 이론적으로 키는 유한하고 불연속적이므로, 키가 무엇이든 간에 음이 아닌 정수로 나타내는 것이 가능하다. 파이썬에서는 hash()를 이용해 정수에 대응시킬 수 있다.(사실 prehash라고 하는 것이 더 정확하다.) hash()에 들어가는 객체는 숫자, 문자열, 튜플, __hash__가 구현된 객체 등이 될 수 있다.
사실 이론적으로 x와 y가 같다면 hash(x)와 hash(y)는 동일해야 하고, 이 반대도 성립해야 한다. 하지만 파이썬에서는 그렇지 않은 경우도 종종 있다.
테이블에서 객체의 키는 바뀌어서는 안되며, 가변 객체 또한 키가 될 수 없다.
이번에는 2번 문제를 해결해보자. 이를 위해서는 해싱을 사용해야 한다. 비로소 진정한 해싱이다. 해싱은 모든 키가 들어있는 전체 집합 U를 합리적인 크기 m인 테이블로 줄이는 것을 말한다.
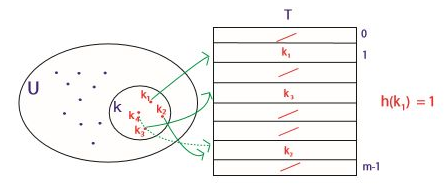
왼쪽 전체 집합 U에 모든 키들이 들어있고, 이 집합은 테이블 T의 키들을 가지고 있다. 그럼 이 키들만을 모아서 그림처럼 부분집합을 만들 수 있을 것이다. 그리고 이 키들을 테이블의 각 위치에 대응시킨다. 이 대응 관계를 해시 함수라고 본다. 예를 들어 $h(k_3) = 3$이라면 $k_3$는 3번째 항목의 키가 된다.
여기서의 아이디어는 테이블의 크기 m을 딕셔너리에 저장된 키의 개수 n(현재 키의 개수)에 비례하게 만드는 것이다($m = \Theta(n)$). 그럼 m개를 저장하고 싶다면 2m 혹은 3m 정도의 공간만 사용해도 된다.
문제가 하나 있다. 만약 $k_1$과 $k_2$가 같은 항목을 가리킨다면? $k_i \neq k_j$ 인데 $h(k_i) = h(k_j)$ 인 경우를 충돌이라고 부른다.
충돌 해결하기 - 체이닝
체이닝(chaining)을 이용하면 충돌을 해결할 수 있다. 체이닝은 테이블의 슬롯마다 충돌하는 원소들의 연결 리스트를 만드는 것을 말한다.
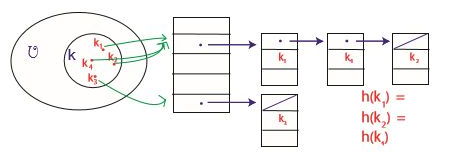
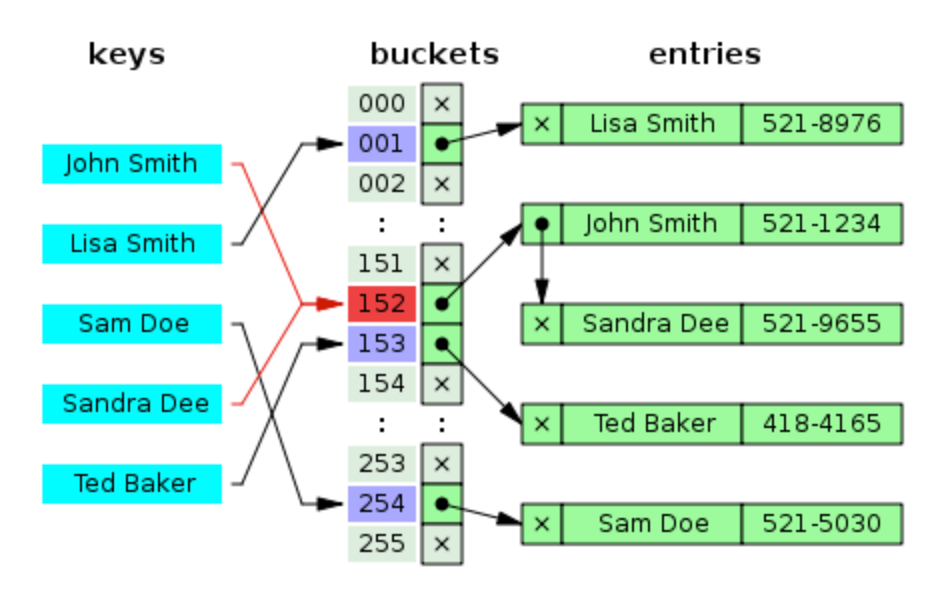
충돌이 일어난 슬롯에 대해 탐색을 한다고 하면 리스트 전체를 훑어야 하고, 최악의 경우에는 모든 n개의 키가 같은 슬롯에 있을 수 있다(…)
체이닝의 이해 - 간단 균일 해싱
간단 균일 해싱은 모든 키가 테이블의 아무 슬롯에나 해시될 가능성을 동일하게 가지고 있다고 보는 동시에, 해당 가능성은 다른 키가 해시되었는지와 상관이 없다고(독립적) 가정한다. 이는 비현실적이지만 체이닝을 설명하는 데는 용이하다.
n을 테이블에 저장된 키의 개수, m을 테이블의 슬롯 개수라고 해보자. 그럼 체인의 예상되는 길이(기댓값)은 무엇일까? 한 슬롯에 들어갈 확률이 $\frac{1}{m}$ 이고, 키가 n개이므로 체인 길이의 기댓값은 $\frac{n}{m}$ 일 것이다. 이를 적재율($\alpha$)이라고 하기도 한다. ($\alpha = \frac{n}{m}$)
탐색의 예상되는 총 실행 시간은 $\Theta(1 + \alpha)$ 가 된다. 1은 해시 함수를 적용하고 슬롯에 임의 접근하는 시간, $\alpha$ 는 리스트 탐색 시간이다. 우리가 해싱의 개념에서 보았듯이 $m = \Theta(n)$ 라면, 총 실행시간에 대해서 $\Theta(1)$ 이 성립한다. 즉, 해싱을 이용하면 탐색을 상수 시간 내에 수행할 수 있는 것이다.
해시 함수 1 - 나머지 연산법
그럼 위와 같은 성능을 달성할 수 있는 해시 함수에는 어떤 것들이 있을까?
해시 값으로 나머지를 사용하는 나머지 연산법이 있다.
h(k) = k mod m
이는 m이 2의 제곱이나 10의 제곱에 가까이 있지 않은 소수라면 실용적이다. 바꿔말하면, 이 경우를 제외하면 그렇게 실용적이지 않다는 의미이다. 당연히 전자의 경우는 별로 없다
해시 함수 2 - 곱셈 방법
h(k) = [(a $\cdot$ k) mod $2^w$] » (w-r)
a는 임의의 값, k는 w비트, m은 $2^r$ 이다. 이건 그림으로 이해해야 더 빠르다.
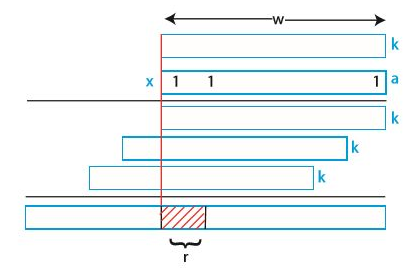
w비트를 가진 k를 a와 곱했다. 그럼 k를 a가 1인 지점마다 반복될 것이다(마치 여러 자릿수의 곱셈처럼). 그리고 이를 모두 더한다(마찬가지로 여러 자릿수의 곱셈처럼). 그 결과에 mod $2^w$를 하라는 의미는 가장 오른쪽의 w비트만 취하라는 의미이다. 그리고 거기에서 w-r만큼 오른쪽으로 이동(»)을 했다. 그럼 위 그림에서 r 부분만이 남게 된다.
이 방법은 a가 홀수이거나, $2^{w-1}$ 과 $2^w$ 사이에 있거나, $2^w$ 에 너무 가깝지 않다면 잘 작동한다. 즉, 나머지 연산법보다 훨씬 유용하다.
왜 작동을 잘 할까? 직관적으로 이해해보자. k를 랜덤하게 섞어서 더하고 잘랐으며, 그 중에서 가장 많이 섞인 부분을 선택했다. 즉, 모든 과정이 매우 랜덤한 것이다. (사실 오늘 배운 개념에 ‘자르고 합치다’라는 의미를 가진 ‘해싱’이라는 명칭이 붙은 것도 이 과정과 무관하지 않다.)
해시 함수 3 - 유니버설 해싱
이건 그냥 이런 게 있다고만 알아두자.
h(k) = [(ak + b) mod p] mod m
a와 b는 0와 p-1 사이의 임의의 값으며, p는 전체 집합보다도 더 큰 소수이다. 해시 값이 같은 최악의 경우에 대한 확률이 $\frac{1}{m}$ 이다.
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기