BST에서의 높이
BST에서의 높이는 단말 노드까지의 가장 긴 하향 경로의 길이로 정의한다.
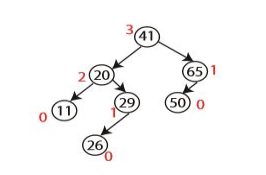
위 예시를 보자. 50인 노드를 보면, 그 자체가 단말 노드이므로 높이는 1이 된다. 루트인 41을 보면 단말 노드까지 가장 먼 단계가 3이므로 높이는 3이 된다. 노드의 높이를 식으로 써보면 다음과 같다.
height = max(height(left child). height(right child)) + 1
단말 노드의 경우 위 식을 적용하기 좀 힘들 것이다. 그래서 우리는 단말 노드들이 높이가 -1인 자식 노드를 가졌다고 보기도 한다.
균형 이진 탐색 트리
앞선 글에서도 살펴 보았지만, BST에서 균형을 이루는 것은 매우 중요하다. BST에서는 삽입, 삭제, 최솟값, 다음으로 큰 값 찾기 등의 작업들이 모두 $O(h)$ 의 시간 안에 진행되기 때문이다. 만약 h가 n과 동일하다면 우리는 이진 탐색 트리를 쓰는 이유가 없을 것이다.
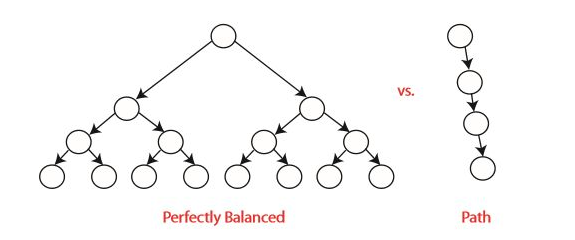
‘균형 잡혔다’는 단순히 모양이 예쁘다(?)는 것이 아니라 h가 $\log{n}$ 이라는 뜻이다. 트리가 균형 잡혔다면 BST에서의 모든 작업은 $O(\log{n})$ 의 시간 안에 완료될 것이다.
AVL 트리
균형 BST의 대표격인 AVL(Adel’s son - Vel’skii & Landis 1962) 트리를 살펴보자. 이 트리는 모든 노드에 대해, 왼쪽과 오른쪽 자식들의 높이 차가 최대 1이다.
\[\vert h_l - h_r \vert \leq 1\]cf. 양쪽 자식의 높이 차를 0으로 만드는 것은 거의 불가능하다. 단말 노드가 정확히 2의 제곱만큼 존재해야하기 때문이다. 하지만 차를 1로 만드는 것은 쉽다.
AVL 트리에서는 각 노드에 자신의 높이를 저장하게 된다.
그럼 이제 AVL 트리에서 왜 모든 작업이 $O(\log{n})$ 의 시간 안에 완료되는지를 알아보자.
먼저, $N_h$ 를 높이가 h인 AVL 트리에서의 노드 개수라고 해보자. $N_h$ 는 점화식으로 쓸 수 있다.
\[N_h = N_{h-1} + N_{h-2} + 1\]왼쪽 자식과 오른쪽 자식의 노드 개수를 더하고, 본인의 노드 개수까지 더하기 때문에 위와 같은 식이 된다.
위 식을 아래와 같이 조금 변형할 수 있다.
\[N_h = N_{h-1} + N_{h-2} + 1 \\ > N_{h-2} + N_{h-2} + 1 \\ > 2N_{h-2}\]그런데 첫번째 줄 어디서 본 것 같지 않은가? 바로 피보나치 수열과 유사하다. 피보나치 수열의 일반항(유도 과정은 생략…)을 끌어와서 다음과 같이 정리할 수 있다.
\[N_h = F_{n+1} - 1 \\ F_h = \frac{\phi^h}{\sqrt{5}}, \; (\phi = \frac{1 + \sqrt{5}}{2})\]따라서 점화식을 조금 더 수정해보면
\[N_h = N_{h-1} + N_{h-2} + 1 \\ > N_{h-2} + N_{h-2} + 1 \\ > 2N_{h-2} \\ = 2^{\frac{h}{2}}\]결론은 다음과 같다.
\[h < 2\log{N_h}\]중요한 것은 h가 상수 $\times$ $\log{n}$ 이라는 사실이다. AVL 트리에서 시간은 최대 $O(\log{n})$ 밖에 걸리지 않는다.
AVL 트리 만들기
AVL 트리가 왜 좋은지를 알았으니, 어떻게 만드는지도 알아야 할 것이다. 기본적으로는 가장 아래 단말 노드에서 시작해서, AVL 조건을 만족하지 않는 트리를 계속 고쳐 나가면 된다.
AVL 트리를 만들 때 핵심이 되는 개념은 ‘회전’이다. x가 AVL을 위반하는 가장 낮은 노드라고 해보자. 오른쪽이 더 무거워서 AVL이 깨지는 상황이고, 그 오른쪽 트리가 오른쪽 무거움이거나 균형이면 다음과 같이 회전을 한다. (화살표는 더 무거운 쪽을 가리킨다.)
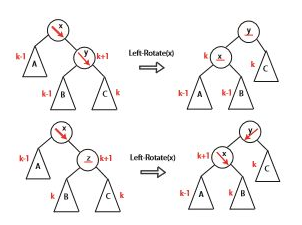
오른쪽이 더 무겁긴 한데, 오른쪽 트리에서는 왼쪽이 더 무겁다면 다음과 같은 회전을 한다.
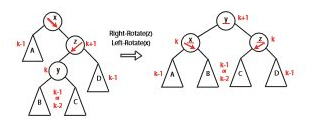
회전에는 상수 시간만이 걸린다.
이 과정을 계속 반복하면서 트리의 윗부분으로 올라가면 된다.
개념만 봐서는 이해가 어려우니 예시를 보자.
다음과 같은 AVL 트리에 23을 넣을 생각이다.
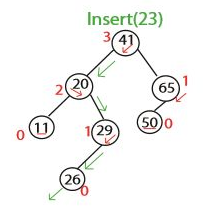
먼저, 그냥 BST에서 23을 넣듯이 삽입한다.
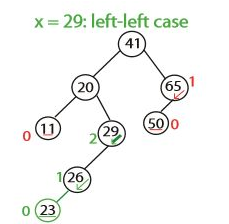
그럼 29 노드에서 균형이 맞지 않는 것을 볼 수 있다. 그럼 회전으로 맞춘다.
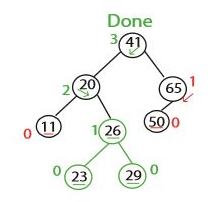
AVL 조건을 만족하는 트리가 완성되었다. 다음은 55를 넣어보자.
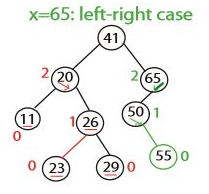
65 노드에서 균형이 맞지 않는다. 그런데 우리가 보던 상황들과 조금 다르다. 어떻게 해야할까? 일단 55와 50을 회전해보자. 그럼 우리가 앞서 23을 삽입했던 상황과 유사해진다. 최종적인 트리는 다음과 같다.
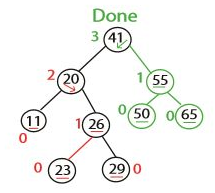
n개의 아이템을 삽입하는 시간은 $\Theta(n\log{n})$ 이다.
AVL 트리를 이용해서 정렬을 수행할 수도 있다. 중위 순회라고 하는데, 큰 값들을 계속적으로 골라내는 것이다. 시간은 $\frac{\Theta(n)}{\Theta(n\log{n})}$ 이다.
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기