정렬을 하는 이유
왜 정렬을 해야할까?
먼저, 우리는 데이터를 활용할 때 정렬된 것을 더 선호한다. 전화번호부와 같은 데이터를 다룰 때 정렬이 되어 있다면 다루기가 더 편리할 것이다.
그리고 정렬을 통해 문제를 더 쉽게 해결할 수 있다. 배열에서 중간값을 찾는다고 해보자. 물론 정렬을 해야만 중간값을 구할 수 있는 것은 아니다. 하지만 정렬이 되어있다면 A[n/2]라는 간단한 과정을 통해 구할 수 있다. 정렬이 되어있다면 이진 탐색을 할 때도 선형 탐색이 로그 탐색이 된다.
또한, 데이터 압축이나 컴퓨터 그래픽에서도 정렬은 유용하게 사용된다.
삽입 정렬
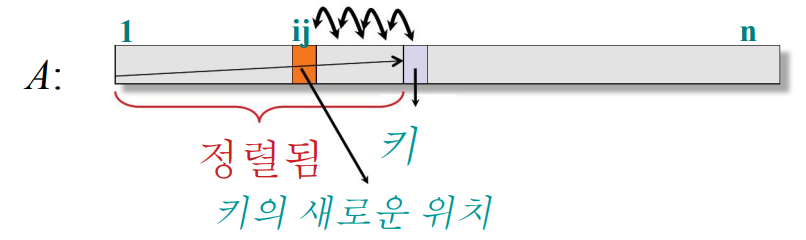
삽입 정렬은 다음과 같은 의사코드로 표현할 수 있다.
for j in range(2, n):
쌍별 스왑으로 키(key) A[j]를 이미 정렬된 보조 배열인 A[1, ..., j-1]에 삽입
쌍별 스왑은 두 숫자를 비교해서 순서대로 배열한다는 의미이다.
의사코드가 이해되지 않는다면 아래 예시를 살펴보자. 우리는 [8, 2, 4, 9, 3, 6]라는 배열을 삽입 정렬로 정렬하고 싶다.
먼저, 2를 key로 지정하고, 2의 앞쪽에 있는 배열인 8과 비교하여 정렬(쌍별 스왑)한다.

그럼 [2, 8, 4, 9, 3, 6]이라는 배열이 생겼다. 다음 key는 4가 된다. 4를 가지고 또 그 앞에 있는 배열과 비교하여 스왑한다.

다음 key는 9가 된다.
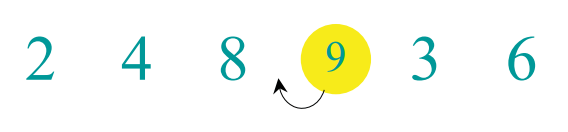
다음 key는 3이 된다. 여기서 중요한 사실은, 3은 쌍별 스왑을 여러 번 해야한다는 점이다.
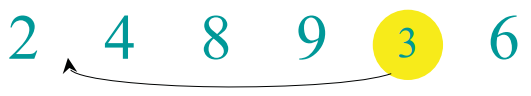
최종 배열은 [2, 3, 4, 6, 8, 9]가 된다.
삽입 정렬에서 실행 시간을 생각해보자. 키의 이동에 $\Theta(n)$, 쌍별 스왑에 $\Theta(n)$ 의 시간이 소요되므로, 최종적으로는 $\Theta(n^2)$ 의 실행 시간이 된다.
여기서는 비교와 스왑의 비용이 비슷하다고 가정했다. 그러나 어떤 경우에는 비교가 더 큰 비용이 들기도 한다. 이럴 경우 이진 탐색으로 비교 과정을 개선할 수도 있으나, 스왑으로 인해 여전히 최종적으로 $\Theta(n^2)$ 의 시간이 걸린다.
합병 정렬
합병 정렬에서 가장 중요한 단어는 ‘재귀’라고 할 수 있다. 배열을 무수히 쪼개 나간 다음 쪼개진 각 배열을 정렬하고, 이를 합치면서 정렬하는 방식이다. 더 정확히 설명하면 다음과 같다.
n개의 요소를 가진 배열에 대해
- n = 1이면 종료.
- 그 외의 경우, A[1 … n/2]과 A[n/2 + 1 … n]을 재귀적으로 정렬.
- 두 정렬된 보조 배열 합병.
예시를 통해 보자. 우리는 배열을 [20, 13, 7, 2]와 [12, 11, 9, 1]로 쪼개고, 쪼개진 배열은 이미 정렬해둔 상태이다.

각 배열에서 가장 작은 숫자인 2와 1을 비교한다. 1이 더 작으므로 1을 새로운 배열에 가장 앞에 둔다.
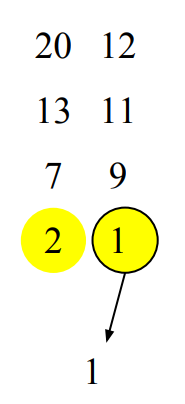
1을 선택한 배열의 다음 작은 숫자는 9이다. 그럼 우리는 2와 9를 비교한다. 2가 더 작으므로 2를 선택한다.
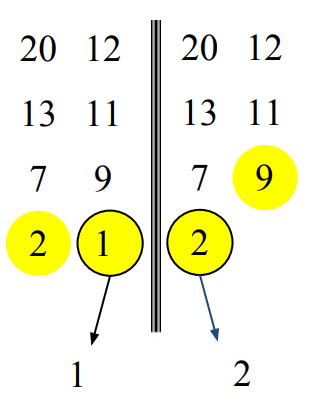
그 다음은 7과 9를 비교하는 차례이다. 7을 선택한다.
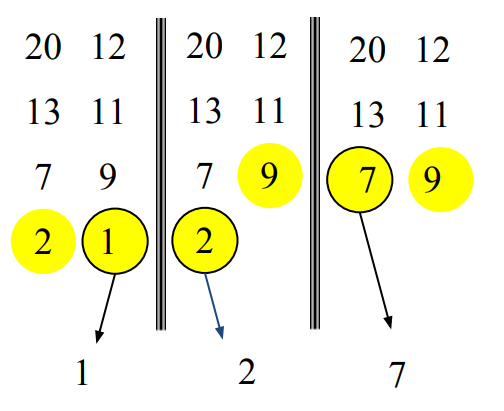
이런 식으로 반복하다보면 결국 [1, 2, 7, 9, 11, 12]라는 정렬된 배열을 얻을 수 있다.
합병 정렬의 재귀적 풀이
합병 정렬에 걸리는 시간을 재귀적으로 풀어보면 다음과 같다.
\[T(n) = c_1 + 2T(n/2) + cn\]c는 $\theta$ 를 대신하는 상수라고 생각하면 된다. $c_1$ 는 배열을 나누는 데 걸리는 시간, $2T(n/2)$ 는 재귀적으로 해결하는 데 걸리는 시간, $cn$ 은 합병하는 데 걸리는 시간이다.
우리는 여기저기서 합병 정렬에서 걸리는 시간이 $\Theta(n\log{n})$ 이라는 것을 들어봤다. 왜 그런지 재귀 트리를 이용해 살펴보자.
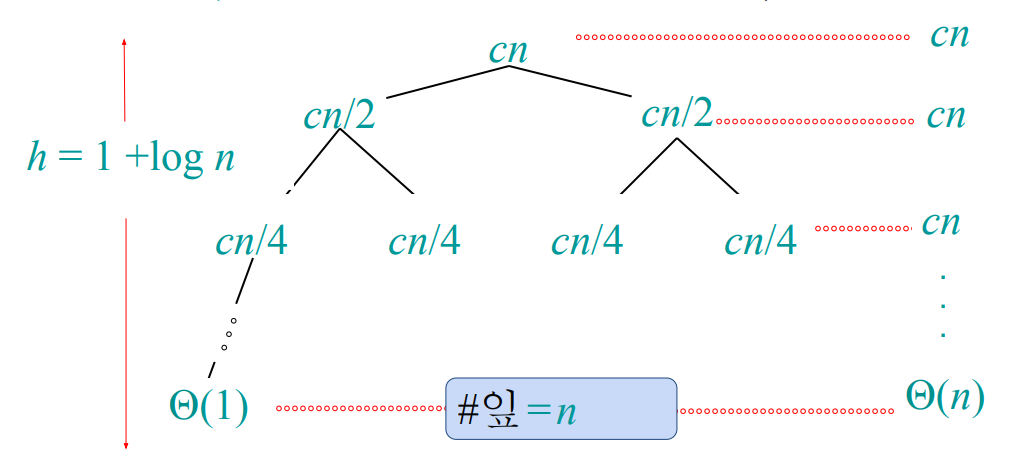
배열을 쪼개는 과정을 트리로 표현했다. 계속해서 배열을 쪼개다보면 결국에는 1개 요소씩만 남을 것이다. 트리는 몇 개의 단계로 구성될까? $1 + \log{n}$ 이다. 가장 마지막 줄에 잎(단말 노드)의 개수는 n개가 될 것이다.
각 단계에서의 일의 양을 생각해보자. 첫 번째 줄에서도 cn, 두 번째 줄에서도 cn, 마지막 줄에서도 cn이다. 즉, 단계에 무관하게 일의 양은 동일하다. 그럼 전체 일의 양을 고려해서 T(n)을 다음과 같이 표현할 수 있다.
\[T(n) = (1 + \log{n}) \cdot cn = \Theta(n\log{n})\]삽입 정렬과 병합 정렬 비교
병합 정렬은 삽입 정렬에 비해 시간 면에서 확실히 이점을 가진다. 그러나 항상 병합 정렬이 좋은 것만은 아니다.
병합 정렬은 ‘재귀’라는 과정을 거쳐야 하고, 이는 새로운 배열을 계속해서 만들어내기 때문에, 보조 공간이 필요하다. 즉, 메모리(공간) 측면에서 단점이 된다. 반면 삽입 정렬은 일정한 공간을 가지는 ‘제자리 정렬’이므로, 공간 측면에서는 병합 정렬에 비해 이점이 있다.
병합 정렬의 단점을 해결하기 위한 ‘제자리 병합 정렬’이 있으나, 이는 시간 측면에서 더 나쁘다(…)
번외: 다른 재귀에 대한 트리
재귀 식이 $T(n) = 2T(n/2) + c$ 이면 어떨까?
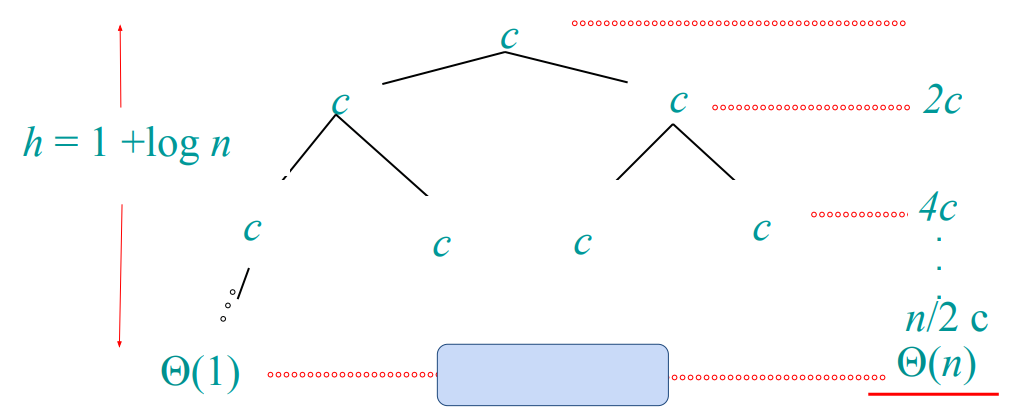
단계가 $1 + \log{n}$ 인 것은 동일하다. 그러나 단계에 따른 일의 양이 다른데, 마지막 단말 노드에서 $n/2 \dot c$ 의 일을 한다는 것을 볼 수 있으며, 그 외의 단계를 모두 더해도 이 노드의 일의 양을 넘지 못한다. 따라서 복잡도는 $\Theta(n)$ 가 된다.
재귀 식이 $T(n) = 2T(n/2) + cn^2$ 인 경우도 보자.
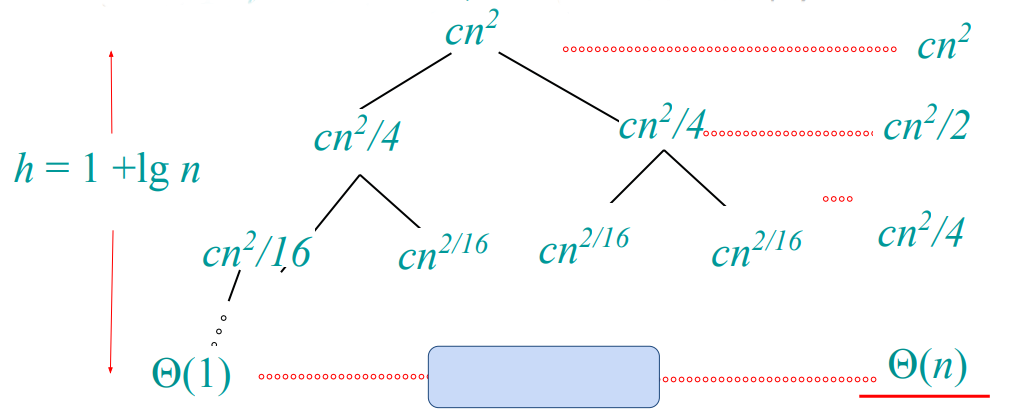
직전 예시와 마찬가지로 단계 수는 동일하다. 하지만 이번에는 나머지 단계의 일을 다 더해도 첫 번째 단계의 일($cn^2$)을 넘지 못한다. 따라서 총합은 $\Theta(n^2)$ 가 된다.
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기