이번 시간에도 동적 프로그래밍의 5단계로 다양한 문제들을 해결해본다.
2종류의 추측
지난 시간 마지막에 살펴본 냅색 문제처럼 정답 구조에 대해 더 많은 것을 기억해야할 때가 있다. 이 때는 하위 문제를 추가해서 해결할 수 있다.
피아노/기타 핑거링
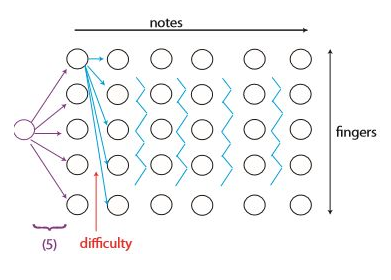
피아노나 기타를 연주할 때 손을 가장 힘들이지 않고 움직이며 연주하고 싶을 것이다. 피아노로 n개의 음 시퀀스를 F개의 손가락(한 손)만으로 연주할 때에 대해 탐구해보자. d(f, p, g, q)는 음 p를 손가락 f로 연주한 다음 음 q를 손가락 g로 연주할 때의 난이도이다.
cf. 여러 제한 조건을 추가할 수도 있다. 예를 들어 한 번에 많은 건반을 넘나드는 것은 불편할 수도 있고, 손가락에 제한을 가하는 다양한 연주 기법을 적용해야할 수도 있다. 또한, 손가락의 구조적 한계 때문에 동시에 두 손가락을 연주하는 것이 불편할 수도 있다!
일단 가장 간단하게 시도해보자.
-
하위 문제로 분류
연속적인 음의 시퀀스이므로 suffix를 사용하면 될 것이다. suffix notes[i:]에 대해 최소한의 난이도(d)를 가지게 해야한다. -
추측
하위 문제의 첫 음 i를 연주하는 것에 어떤 손가락을 사용해야 하는지를 추측한다. -
재귀
재귀 식은 다음 음에 대한 난이도와 음 i에 대한 난이도를 합한 ‘DP[i] = min(DP[i + 1] + d(note[i], f, note[i + 1, ?]))’이 된다. 문제는 다음 음을 무슨 손가락으로 연주할지를 알 수가 없다.
야심차게 동적 프로그래밍을 시도했지만 재귀 식에서 막히고 말았다. 다음 음에 대한 정보가 부족해서 더 이상 진행할 수 없는 상태이다. 이를 조금 개선해보자.
-
하위 문제로 분류
아까와 다르게 손가락에 대한 정보를 추가해보자. i번째 음을 손가락 f로 연주할 때 suffix notes[i:]의 난이도 최솟값을 하위 문제로 정한다. 그럼 $n \cdot F$ 개의 하위 문제가 생긴다. -
추측
다음 i+1 번째 음을 어떤 손가락(g)으로 연주할지를 추측한다. F개의 선택지가 있다. -
재귀
재귀 식은 ‘DP[i, f] = min(DP[i + 1, g] + d(note[i], f, note[i + 1], g))’ 이 된다. g에 대한 선택지는 F개가 있음을 다시 상기한다. 따라서 하위 문제당 시간은 $\Theta(F)$ 이다. 또한, DP[n, f] = 0 이다. -
순서
i에 대한 반복(range(n))이 우선 이루어지고, 그 안에서 f에 대한 반복(range(1, F + 1))이 이루어지는 형태이다. 총 시간은 $O(nF^2)$ 이다. -
기존 문제
지금까지 봤던 기존 문제들과 조금 다르다! 우리는 처음에 무슨 손가락으로 연주했는지를 알 수 없고, 그 것조차 정해주어야 한다! 따라서 기존 문제는 min(DP[0, f]) 가 된다.
이 문제를 DAG로 나타낼 수 있다. 노드 사이의 간선들은 난이도(d)를 나타낸다.
피아노가 아니라 기타의 경우에는 동시에 여러 줄을 연주할 수 있으므로 F 대신 줄의 개수 S를 곱한 $F \cdot S$ 를 사용한다.
한 번에 여러 개의 음을 연주하는 화음의 경우에는 최대 F개 음의 리스트를 가진다. 각 손가락에서는 아무 것도 연주하지 않는 상태를 더하여 (F+1) 개의 상태가 가능하고, 모든 손가락을 고려하면 전체적으로 $(F+1)^F$ 개의 상태가 가능하다. 따라서 $n \cdot (F+1)^F$ 개의 하위 문제, $(F+1)^F$ 개의 선택, $n \cdot (F+1)^{2F}$ 의 총 시간이 소요된다.
테트리스 문제
테트리스 문제도 동적 프로그래밍으로 해결할 수 있다. 일단 몇 가지 조건이 필요하다.
- n개의 테트리스 조각과 작은 폭 w의 보드가 주어짐(w는 매우 작음).
- 회전 정도(4가지)와 x좌표를 정해야함.
- 조각이 다른 조각이나 바닥에 닿을 때까지 떨어뜨림.
- 꽉 찬 행은 지우지 않음.
이게 테트리스냐
우리의 목표는 당연히 살아남기이다. 다른말로 하면 높이 h 내에서 유지하기라고도 볼 수 있다.
일단 시도하기 전에 한 번 생각해보자. 앞에서도 데인 적이 있으니 우리는 테트리스 한 조각을 놓을 때, 그 조각 뿐만 아니라 보드의 상태가 어떠한지도 신경을 써야 한다. 즉, 정보가 더 추가되어야 한다. 이를 유념하며 하위 문제를 정해보자.
-
하위 문제로 분류
보드의 시퀀스가 있으므르 suffix를 사용할 수 있다. suffix [i:] 에서 생존하는 것이 하위 문제이고, 초기 열이 채워진 정보 h가 주어져야 한다. 여기서 h는 보드에 이미 존재하는 조각들의 높이 정보(skyline)라고 볼 수 있다. w개의 가로 칸(폭) 각각에 대해 h개의 높이가 가능하므로 하위 문제의 개수는 $O(n \cdot h^w)$ 가 된다. -
추측
i번째 조각을 어떻게 떨어뜨릴지를 추측한다. 회전까지 고려하면 $4 \cdot w$ 개의 선택지가 있다. -
재귀
‘DP[i, h] = max(DP[i, m])’의 재귀식이 된다 (물론 유효한 이동에 대해서이다). 하위 문제의 시간은 $O(w)$ 이다. -
순서
앞선 피아노 문제와 같은 순서를 가진다. 총 시간은 $O(nwh^w)$ 이다. -
기존 문제
DP[0, 0]을 구한다.
슈퍼 마리오 브라더스
초창기 슈퍼 마리오 브라더스 게임도 동적 프로그래밍으로 탐구할 수 있다. 일단 다음과 같은 상태이다.
- 주어진 레벨에는 n비트의 정보가 있음.
- w $\times$ h의 작은 화면.
게임 상태는 다음과 같다.(괄호 안은 정보의 양이다.)
- 화면 이동(n)
- 플레이어의 위치 & 속도(w)
- 오브젝트의 상태, 몬스터의 위치($c^{w \cdot h}$)
- 화면 밖의 모든 것은 초기 상태로 돌아감.($c^{w \cdot h}$)
- 점수(S)
- 시간 제한(T)
-
하위 문제로 분류
우리의 목표는 게임 상태 C에서 최고의 점수를 얻는 것이다. $n \cdot c^{w \cdot h} \cdot S \cdot T$ 개의 하위 문제가 있다. -
추측
상태 C에서 할 다음 행동이다. O(1)의 선택지가 있다. -
재귀
DP(C)는 3가지가 가능하다. 먼저, 시간이 남지 않거나 죽으면 $\infty$ 가 된다. 다음으로 목적지(flag)에 도달하면 점수를 반환하는 C.score가 된다. 둘 다 아니라면? 행동 A에 대해 max(DP($\delta(C, A)$)) 가 된다. ($\delta(C, A)$ 는 상태 C에서 행동 A를 했을 때 다음 게임 상태이다.) -
순서
시간의 오름차순이 된다. -
기존 문제
DP(초기의 게임 상태) 이다.
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기