깊이 우선 탐색
깊이 우선 탐색은 미로를 탐험하는 것과 같다. 우리는 미로를 풀 때 막다른 길에 다다르면 교차로로 다시 돌아와서 다른 길을 선택한다. 깊이 우선 탐색도 마찬가지다. 알고리즘을 조금 더 다듬으면 다음과 같다.
- 막다른 골목까지 경로를 탐색한다.
- 탐색되지 않은 이웃(Adj)에 도달할 때까지 역추적한다.
- 재귀적으로 탐색한다.
- 정점을 반복하지 않도록 조심한다.
예시를 살펴보자.
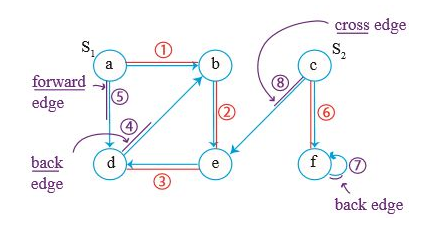
먼저 a에 대해 탐색을 해보자. a에서 나가는 간선은 b로 가는 것밖에 없으므로 b로 이동한다. 그 다음엔 e로, 다음엔 d로밖에 갈 수 없다. d에서 나가는 간선은 b로 이어지지만, b는 이미 방문했으므로 더 이상 갈 곳이 없다. 따라서 parent인 e로 이동한다. e에서 또한 더 이상 갈 곳이 없으므로 b로 거슬러 올라가고, 다시 a로 가게 된다.
b는 이미 탐색했으므로 건너 뛴다. c는 어떨까? 먼저 f로 간다고 해보자. f에서 나가는 간선은 하나 인데, 이미 탐색한 f로 돌아오므로 끝났다. c에서는 e로도 갈 수 있지만, 이 역시 이미 탐색한 상황이기 때문에 더 이상 할 수 있는 것이 없다. 다른 정점도 이미 한 번씩 방문한 상태이기 때문에 알고리즘이 마무리 된다.
의사코드로도 알아보자.
parent = {s: None} # 1
DFS-visit(Adj, s):
for v in Adj[s]: # 2
if v not in parent: # 3
parent[v] = s
DFS-visit(Adj, v)
DFS(V, Adj):
parent = {}
for s in V: # 4
if s not in parent: # 5
parent[s] = None
DFS-visit(Adj, s)
일단 부모 정점을 담을 parent를 만들었다(# 1). 그 다음 코드는 두 개의 파트로 나누어져 있는데, 1번 파트는 특정 정점 s에서의 탐색을 나타낸 것이고, 2번 파트는 전체 그래프를 탐색하기 위한 코드이다.
1번 파트에서는 먼저 정점 s에 대해 인접 정점들을 탐색한다(# 2). 만약 인접 점(v)이 parent에 들어있지 않다면 s를 부모로 하고 v에 대해 재귀적으로 다시 탐색한다(# 3).
2번 파트에서는 모든 정점에 대해 반복문을 돌린다(# 4). 만약 s가 parent에 없다면 s의 parent를 None으로 설정하고 s에 대해 DFS(DFS-visit(Adj, s))을 실행한다(# 5).
깊이 우선 탐색에 걸리는 시간은 선형시간인 O(V + E)로, 너비 우선 탐색과 동일하다. 유도 과정은 방문 시간인 $\displaystyle \sum_{s \in V}{\vert Adj[s] \vert} = O(E)$ 에 정점 탐색 시간인 O(V)를 더하면 된다.
간선 분류
깊이 우선 탐색이 너비 우선 탐색에 비해 유리한 상황은 크게 두 가지가 있다. 이를 알기 위해서는 먼저 간선 분류에 대해 알아야 한다.
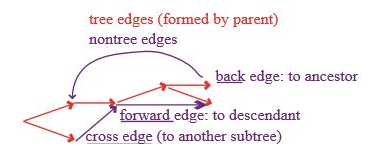
그래프에서 깊이 우선 탐색을 하면 정점들 사이에 부모와 자식 관계가 나타나게 되고, 이를 마치 트리처럼 생각할 수 있다. 탐색을 하는 과정에서 어떤 간선이 방문하지 않은 정점으로 이끌면 이를 트리 간선이라고 한다. 트리 간선이 아닌 것들은 아래와 같이 분류할 수 있다.
- 트리 간선: 방문하지 않은 정점으로 이끄는 간선.
- 순방향 간선: 부모에서 자식으로 가는 간선. 트리 간선인 경우는 제외.
- 역방향 간선: 자식에서 부모로 가는 간선.
- 교차 간선: 부모-자식 관계가 없는 두 서브 트리 간의 간선. 트리 간선, 순방향, 역방향이 모두 아닌 경우에 해당한다.
이 분류를 계산하기 위해서는 정점에 탐색 시각을 표시하거나 횟수를 세는 카운터를 설정해줄 수 있다.
참고로 무뱡항 그래프에서는 트리 간선과 역방향 간선만이 존재한다. 무방향 그래프에서는 한 간선이 순방향 간선으로 정해지기 전에 이미 역방향 간선이 되어버리므로 순방향 간선이 존재할 수 없다. 교차 간선 역시 존재하지 않는다.
순환 검출
그래프 G가 순환(cycle)이 있다는 것은 깊이 우선 탐색에서 역방향 간선이 있다는 것의 필요충분조건이다. 증명해보자.
먼저 역방향 간선이 있으면 순환이 있다는 것을 증명해보자. 아래 그림처럼 간단하게 증명이 가능하다.
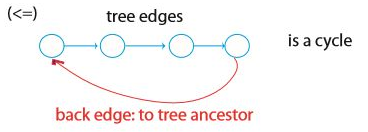
순환이 있으면 역방향 간선이 있다는 사실은 조금 더 복잡하게 증명된다.

먼저, $v_0$ 에 대해 탐색한다고 해보자. 그럼 우리는 $v_k$ 에 대해서도 탐색을 하게 될텐데, $v_k$ 에 대한 모든 탐색이 끝나야만 $v_0$의 탐색을 마무리지을 수 있다. 탐색 과정을 괄호로 생각한다면, $v_0$의 괄호를 먼저 열고 $v_k$의 괄호를 열게 되지만, $v_k$ 가 닫힐 때까지 $v_0$의 괄호를 닫을 수 없다. 즉, ($v_k$, $v_0$) 간선은 역방향 간선이 된다.
결론은 다음과 같다.
그래프 G가 순환이 있다. $\Leftrightarrow$ 깊이 우선 탐색의 역방향 간선이 있다.
잡 스케줄링과 위상 정렬
방향이 있는 비순환성 그래프(Directed Acycle Graph, DAG)가 주어지고 정점이 할 일, 간선은 의존 상태를 의미할 때, 잡 스케줄링을 통해 의존 상태를 위반하지 않고 할 일을 정렬할 수 있다. 쉽게 말해, 그래프를 정렬에 사용할 수 있다.
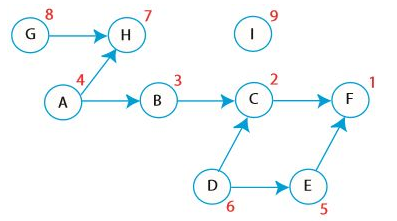
위 그래프에서 정점들이 해야할 일들이고, 간선이 그 일들 사이의 관계라고 할 수 있다. 간혹 I처럼 다른 것과 아무 관련이 없는 일(ex. 손목 시계 차기)도 있을 수 있다. 깊이 우선 탐색을 하면 정점마다 탐색이 마무리 되는 시간을 기록할 수 있다. 그 마무리 시간이 오래된 것(탐색이 가장 먼저 끝난 정점)을 가장 나중으로 미루면(reverse(), 역을 취하는 것이다) 가장 먼저 해야하는 일을 찾을 수 있다.
잡 스케줄링과 위상 정렬의 그래프는 순환 그래프가 아니고, 따라서 역방향 간선이 나타나지 않는다. 증명은 정확성(Correctness)을 이용해서 할 수 있다.

위 간선(u, v)에 대해서, u는 v 이전에 정렬된다는 사실을 증명하고 싶다. v가 u 이전에 끝난다는 사실 말이다. 두 가지로 나누어서 증명해보자. 만약 v전에 u가 방문된다면? 우리가 증명하고 싶은 바로 그 사실이다. 그럼 만약 u전에 v가 방문된다면? 잡 스케줄링과 위상 정렬의 그래프는 비순환 그래프라고 했고, 따라서 v에서 u로 도달할 방법은 없다. 그 말은 u를 방문하기 전에 v의 방문이 끝났다는 뜻이다.
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기