무리수
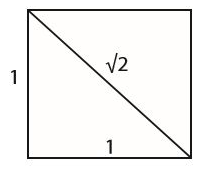
피타고라스 학파가 정사각형에서 대각선을 유리수로 표현할 수 없다는 사실을 알고는 매우 절망했다는 이야기는 유명하다. 위 그림에서처럼 정사각형의 대각선은 무리수인 $\sqrt{2}$ 로 표현할 수 있다. $\sqrt{2}$ 를 제곱근 기호를 사용하지 않는다면 특정한 패턴을 찾을 수 있을까?

패턴 따위는 없어 보인다…
카탈란 수
괄호만을 이용한 문자열을 통해 카탈란 수에 대해 알아보자.
올바른 괄호 구조 문자열(괄호가 열렸으면 제대로 닫힘을 의미, ex ‘(( ))’)로 이루어진 집합 P는 아래와 같이 귀납적으로 정의한다.
- $\lambda \in P$ ($\lambda$ 는 빈 문자열)
- 만약, $\alpha$, $\beta$ $\in P$ 이면, ($\alpha$)$\beta$ $\in P$ 이다.
즉, $\alpha$ 와 $\beta$ 를 이용해 다음 문자열을 계속해서 만들어 낼 수 있다. 예를 들어, $\alpha = ()$, $\beta = ()()$ 이면, $(())()()$ 도 P에 속하는 문자열이다.
$C_{n}$을 n쌍의 괄호를 가지는 올바른 괄호 구조 문자열의 개수라고 해보자. $C_{n+1}$ 은 규칙 2로부터 얻어지는 (n+1)쌍의 괄호를 가진 올바른 괄호 구조의 모든 문자열의 개수다. 예를 들어, $C_0 = 1$, $C_1 = 2$ 가 될 것이다.
$C_2$ 는 어떨까? $C_0$ 과 $C_1$ 의 조합으로 표현할 수 있다.
\[C_2 = C_0 C_1 + C_1 C_0 = 2\]실제로 2개의 괄호를 활용하는 방법은 ‘()()’, ‘(())’ 처럼 2개가 있다.
이처럼 귀납적으로 규칙을 찾아서 $C_{n+1}$ 을 $C_{n}$ 으로 일반화할 수 있다.
\[\displaystyle C_{n+1} = \sum_{k=0}^{n}{C_{k}C_{n-k}} \; (n \geq 0)\]이렇게 얻어지는 숫자들을 카탈란 수라고 한다. 카탈란 수를 조금 나열해보면 다음과 같다.

뉴턴 방법으로 무리수 구하기
이제 다시 무리수로 돌아오자. 뉴턴은 미적분의 창시자로 유명한데, 그의 명성을 빌려서 무리수를 구할 수 있다. 여기서는 접선을 이용하는 연속 근사법을 알아볼 것이다.
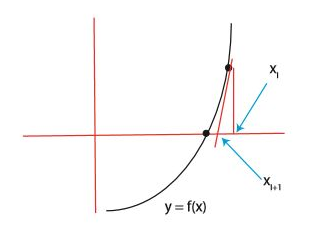
$f(x) = x^2 - a$ 가 있을 때, $x_i$ 에서의 접선의 방정식은 $y = f(x_i) + f^{\prime}(x_i) \cdot (x - x_i)$ 가 된다. 해당 접선의 x절편을 $x_{i+1}$ 라고 할 때, $x_{i+1}$ 는 다음과 같이 나타낼 수 있다.
\[x_{i+1} = x_i - \frac{f(x_i)}{f^{\prime}(x_i)}\]그럼 이제 제곱근을 구해보자.
\[x_{i+1} = x_i - \frac{(x_i^2 - a)}{2x_i} = \frac{(x_i + \frac{a}{x_i})}{2}\]만약 2의 제곱근을 구하고 싶다면 a=2 로 놓으면 된다.

뉴턴 방법은 계산을 1회 늘릴 때마다 정확하게 계산되는 자릿수가 2배 증가하는 이차적 수렴이다. 뉴턴 방식에서 $\frac{a}{x_i}$ 를 정확하게 계산하기 위해서는 고정밀 나눗셈을 해야 한다. 그런데 사실 나눗셈은 곱셈과 비슷한 과정이므로, 서브루틴으로 고정밀 곱셈을 먼저 알아본다.
고정밀도 곱셈
고정밀도 계산에는 정수가 필요하기 때문에 무리수를 d자리의 정수로 바꾸는 과정을 먼저 진행한다. ($10^d \sqrt{2} = \sqrt{2 \cdot 10^{2d}}$)
두 개의 n자릿수 숫자를 곱하는 과정을 알아보자. (n은 2진수 또는 10진수이고, r은 2 또는 10이다.) 먼저, x와 y에 조금 변형을 가해줄 것이다.
\[0 \leq x, \, y < r^n \\ x = x_1 \cdot r^{\frac{n}{2}} + x_0 \\ y = y_1 \cdot r^{\frac{n}{2}} + y_0 \\ 0 \leq x_0, \, x_1 < r^{\frac{n}{2}} \\ 0 \leq y_0, \, y_1 < r^{\frac{n}{2}}\]$x_1$ 은 x의 높은 자릿수 절반, $x_0$ 은 낮은 자릿수 절반이다. 예를 들어 x=123456이면, $x_1$ 은 123, $x_0$ 은 456이 된다. y도 마찬가지.
그리고 곱셈을 하면 다음과 같이 된다.
\[z = x \cdot y = x_1 y_1 \cdot r^n + (x_0 \cdot y_1 + x_1 \cdot y_0) r^{\frac{n}{2}} + x_0 \cdot y_0\]위 곱셈의 시간을 얼마나 걸릴까? 절반 크기를 가지는 숫자들을 4번 곱셈으로 계산한다. 따라서 $\Theta(n^2)$ 의 시간이 걸린다. 점화식은 $T(n) = 4 \times T(\frac{n}{2}) + \Theta(n)$ 이다(덧셈은 선형 시간이 걸린다고 가정).
카라추바 알고리즘
조금 더 발전된 알고리즘은 없을까? 카라추바라는 사람이 알고리즘을 개발했다.
앞서 배운 곱셈식에서 $z_2 = x_1 y_1$, $z_1 = (x_0 \cdot y_1 + x_1 \cdot y_0)$, $z_0 = x_0 \cdot y_0$ 라고 해보자. 카라추바 알고리즘은 다음과 같다.
\[z_0 = x_0 \cdot y_0 \\ z_2 = x_1 \cdot y_1 \\ z_1 = (x_0 + x_1) \cdot (y_0 + y_1) - z_0 - z_2 = x_0 y_1 + x_1 y_0 \\ z = z_2 \cdot r^n + z_1 r^{\frac{n}{2}} + z_0\]먼저 $z_0$, $z_2$ 를 구하고 그 다음에 $z_1$ 를 구했더니 곱셈 횟수가 3회로 감소했다. 점화식은 다음과 같아진다.
\[T(n) = 3T(\frac{n}{2}) + \Theta(n) = \theta(n^{\log_2{3}}) = \theta(n^{1.5849625})\]$\Theta(n^2)$ 보다는 지수가 작아졌다. 시간이 더 적게 걸린다는 뜻이다.
흥미로운 기하학 문제
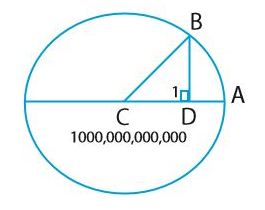
위 그림에서 BD = 1 일때, AD의 길이를 어떻게 구할까? 피타고라스 정리를 이용하면 다음처럼 간단(?)하게 구할 수 있다.
\[AD = AC - CD = 500,000,000,000 - \sqrt(500,000,000,000^2 - 1)\]AD의 길이를 수백만 자리까지 정밀하게 계산하면 놀랍게도 카탈란 수가 나온다.
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기