지난 시간에 이어 정규분포를 주로 다룬다.
정규분포
정규분포는 확률밀도함수(PDFs)로 정의된다. 확률밀도함수에서는 확률 변수가 두 값 사이의 구간에 있을 확률을 구할 수 있다. 바로 ‘적분’을 이용해서다. 그래프에서 살펴보면, 그래프 아래의 면적이 해당 구간에 존재할 확률을 가리킨다.
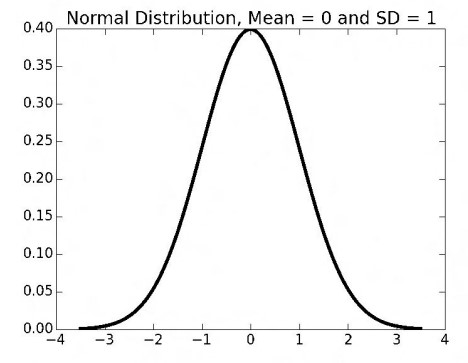
확률밀도함수의 그래프에서 y축의 값은 확률이 아니다! 이들의 밀도이다. 다시 말해(조금 더 어렵게 말해), 누적분포함수의 도함수에 해당한다.
y축의 값은 확률이 아니므로 그냥 y값을 읽는다고 해서 확률을 알 수는 없다. 적분을 이용해 넓이를 구해야 한다.
SciPy 라이브러리를 활용하면 파이썬에서 적분을 수행할 수 있고, 지난 시간에 배운 ‘경험적인 규칙’도 실제로 맞는지 검증해볼 수 있다.
정규분포는 일상생활에서 찾기가 매우 쉽다. 사람의 키의 분포, 시험 점수 분포 등도 거의 정규분포를 따른다.
그러나 지난 시간에 본 룰렛은 정규분포가 아닌 균등분포이다. 룰렛을 한 번 시행했을 때 모든 숫자가 나올 확률이 동일하기 때문이다. 그런데 룰렛을 설명할 때 정규분포의 ‘경험적인 규칙’을 활용하였다. 뭔가 이상하지 않은가?
결론부터 말하면, 룰렛에 정규분포를 적용할 수 있는 이유는 룰렛에서 탐구하고자 하는 것이 한 번의 시행이 아닌 여러번의 시행의 평균에 관한 것이기 때문이다. 중심극한정리로 이를 더 자세히 설명할 수 있다.
중심극한정리
표본이 충분히 큰 경우 다음을 만족한다.
- 표본 집합에 있는 표본들의 평균(표본평균, 표본들의 평균이지 전체의 평균이 아니다!)은 거의 정규분포를 따른다.
- 이 정규분포의 평균은 모집단의 평균(전체의 평균)에 가깝다.
- 표본평균은 분산은 모집단의 분산을 표본의 크기로 나눈 값에 가깝다.
이를 중심극한정리(CLT)라고 한다.
코드를 사용해 중심극한정리를 살펴보면 놀라운 사실(별로 놀랍지도 않지만)을 알 수 있다. 충분히 큰 표본을 이용해 모집단의 평균을 추정하면 중심극한정리에 의해 ‘경험적인 규칙’을 적용할 수 있다는 것이다.
뷔퐁-라플라스 방법
원주율 파이($\pi$)를 추정하기 위해 매우 많은 수학자들이 오랜 시간 노력해왔다. 그 중 ‘뷔퐁-라플라스’는 조금 특이한 방법을 채택했다.
한 변의 길이가 2인 정사각형 안에 꽉 차게 원이 들어있다. 여기에 바늘을 무작위로 떨어뜨리는 실험을 진행한다. 사각형의 넓이와 원의 넓이는 아래와 같다.
\(A_S=2 \times 2 = 4\)
\(A_C = \pi r^2\)
바늘은 던진 뒤 관련 수식은 아래와 같다(기하학적 확률을 일부 사용한다).
\(\frac{원 안의 바늘 수}{사각형 안의 바늘 수} = \frac{원의 넓이}{사각형의 넓이}\)
수식의 원의 넓이에 공식을 대입하면 $\pi$값을 구할 수 있을 것이다. (교수님이 직접 대학원생들을 세워놓고 실험한 동영상이 있다….)
시뮬레이션 코드에서는 이 다음에 정규분포 확률밀도함수를 사용하여 원하는 신뢰도까지 실험을 진행하도록 한다.
그러나 이 시뮬레이션으로는 실제 원주율 값이 아니라, 시뮬레이션에서의 원주율 값을 알 수 있다. 통계적으로 유효한 것과 사실은 엄연히 다르다. 만약 코드 사이에 조그만 버그가 있다고 하면, 설령 값은 비슷할 지언정 실제 원주율 값은 아닌 것이다.
적분값 추정
적분값을 추정하는 유용한 방법 중에 하나는 점을 사용하는 것이다.
임의의 영역 R의 넓이를 추정할 때 다음과 같이 구할 수 있다.
- R을 완전히 포함하며 구하기 쉬운 영역 E를 선택한다.
- E에 속하는 임의의 점들을 선택한다.
- 그 중에서 R안에 있는 점의 비율이 F라고 하자.
- E의 넓이에 F를 곱한다.
위에서 본 뒤퐁-라플라스 방법과 비슷하다.
포스트에 사용된 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기