몬테 카를로 시뮬레이션
몬테 카를로 시뮬레이션은 추정 통계학을 이용하여 알 수 없는 값을 추정하는 방법이다. 다음은 추정 통계학의 기본적인 용어이다.
- 모집단: 예시 집합
- 표본: 모집단의 적당합 부분집합
무작위로 추출한 표본은 모집단과 동일한 특성을 가진다. 즉, 모집단을 모두 조사하기 힘들다면 무작위로 추출한 표본을 사용할 수 있다.
동전을 하나 던진다고 가정하자.
한 번 던져서 앞면이 나왔다고 해서 다음에 무조건 앞면이 나올 것이라고 생각하는 사람은 아무도 없을 것이다. 열 번도 마찬가지다. 100번 정도 던져서 모두 앞면이 나와야 다음에도 무조건 앞면이 나올 것이라고 생각할 수 있다. 사실 그래도 뒷면이 나올 가능성을 생각하지 않을 수 없다
이 예시는 무엇이 예측의 신뢰도에 영향을 주는지 알 수 있다. 바로 ‘표본의 크기’와 ‘표본의 분산’이다. 앞선 예시가 많을수록 예측의 신뢰도가 올라가고, 그 예시가 (앞면만 나온 것처럼 분산되어 있지 않을수록 예측의 신뢰도가 올라간다.
룰렛
룰렛은 카지노에서 사용하는 도구로, 주사위처럼 하나의 숫자를 반환한다. 반환될 숫자를 정확히 예측하는 돈을 얻는 것이다. 숫자는 (공정한 경우) 1~36까지 있다.
큰수의법칙
큰수의 법칙은 각 실행에서 특정 결과가 나올 실제 확률이 p로 동일한 독립 사건이 반복되면, 실행 횟수가 무한대로 갈수록 p와 다른 결과가 나오는 횟수의 비율이 0으로 수렴한다는 것이다.
쉽게 말해, 시행을 많이 할수록 수학적으로 계산한 확률에 가까워진다.
도박사의 오류
얼마 전, 한 야구 해설위원이 3할을 치는 타자가 앞선 세 타석에서 안타를 하나도 치지 못하자, ‘이제 확률적으로 안타를 칠 때가 됐죠?’라고 말하여 네티즌이 갑론을박을 한 적이 있었다.
이러한 오류는 일상생활에서 쉽게 범할 수 있는 오류이다. 수학적으로 3할을 치는 타자가 세 타석 모두 안타를 치지 못할 확률은 $ 0.7 \times 0.7 \times 0.7 $ 이다. 그러나 앞선 해설의 상황은 다르게 생각해야 한다. ‘앞선 세 타석 안타를 치지 못한 3할 타자가 다음 타석에서 안타를 칠 확률’이기 때문이다. 이 경우, 확률은 이전 사건의 영향을 받지 않는 독립적인 사건이기 때문에 0.3이 된다.
도박사의 오류는 뒤이어 나올 ‘평균으로의 회귀’와 헷갈릴 수 있다. 먼저 평균으로의 회귀를 살펴보자.
평균으로의 회귀
‘평균으로의 회귀’는 극단적인 사건 다음에 오는 임의의 사건은 덜 극단적인 경향이 있다는 것을 말한다.
예를 들어, 공정한 룰렛을 10번 돌려서 모두 빨간색이 나온 경우(확률 1/1024), 다음 10번에서는 빨간색이 10번보다 적게 나온다. 수학적으로 계산한 기댓값에 더 가까워지는 것이다.
‘도박사의 오류’와 무엇이 다른지 헷갈릴 수 있다. 교수님도 이 부분에 시간을 많이 할애하여 설명하였다. 머리 좋은 MIT 학생도 이해하기 어려워하더라 다른 점은 다음처럼 정리할 수 있다.
- 도박사의 오류: 극단적 사건 다음에 벌어지는 사건의 확률이 평균보다 적게 나올 것이라고 생각하는 것.
- 평균으로의 회귀: 극단적 사건 다음에 벌어지는 사건이 전체 평균을 수학적 평균에 가까워지도록 할 것이라고 생각하는 것.
즉, 평균 아래로 예측하느냐, 평균에 가까워질 것이라고 예측하느냐의 차이이다.
표준편차, 신뢰도와 신뢰구간
여기서 드는 의문은, ‘도대체 얼마나 많은 표본을 추출해야 예측을 신뢰할 수 있을까’이다.
이에 대한 답을 하기 전에, 표준편차, 신뢰도와 신뢰구간에 대해 알아야 한다.
표준편차는 분산의 제곱근이다. 이상치가 표준편차에 영향을 줄 수 있다는 사실은 알고 있는 것이 좋다. 또한, 표준편차는 그 값 자체로는 의미가 없으며, 항상 평균과 비교하여 그 의미를 파악해야 한다.
신뢰 구간은 말 그대로 ‘구간’이다. 예측의 결과를 특정 값으로 한정하는 대신, 예측에 대한 결과 범위와 그에 해당하는 신뢰도를 제공하는 것이다.
예를 들어, ‘룰렛을 100만번 돌린 결과가 -3.3%이다. 오차 범위는 $\pm$3.5%이고 신뢰도는 95%이다’라는 설명이 있다고 하자. 이를 해석하면 룰렛을 100만번 돌렸을 때, 결과의 기댓값은 -3.3%이고, 95%의 경우는 -6.8%와 0.2% 사이의 결과가 나온다는 뜻이다.
이 확률은 ‘경험적인 규칙’으로 구한다. 경험적인 규칙의 가정에는 두 가지가 있다.
- 평균 추정 오차가 0이다. (오차에 편향이 없는, 결과가 어느 한 쪽으로 무조건 쏠리는 경우가 없다는 뜻.)
- 추정 오차가 정규분포를 가진다.
이 가정하에 생긴 경험적인 규칙은 다음과 같다.
- 데이터의 ~68%는 평균으로부터 1표준편차 이내에 존재
- 데이터의 ~95%는 평균으로부터 1.96표준편차 이내에 존재
- 데이터의 ~99.7%는 평균으로부터 3표준편차 이내에 존재
위의 경험적인 규칙은 확률밀도함수로 정의되는 연속확률분포로부터 구할 수 있다. 그래프 아래 영역의 넓이가 그 범위의 확률이 된다.
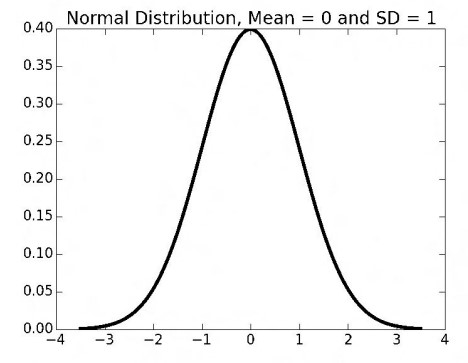
포스트에 사용된 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기