그래프
일반적으로 ‘막대 그래프’, ‘선 그래프’ 등의 표현을 많이 사용한다. 하지만 여기서 사용하는 그래프는 그 형태가 좀 다르다.
지금부터 살펴볼 그래프는 ‘노드(Node)’와 ‘엣지(Edge)’로 이루어져 있다. Node는 꼭짓점으로 정보를 담는 역할을 하고, Edge는 이러한 Node를 연결한다. 최종적으로 그래프는 Node의 집합이라고 하겠다.
Edge는 방향이 있을 수도 있고, 없을 수도 있다. 방향이 있는 그래프를 유향 그래프(Directed-graph), 방향이 없는 그래프를 무방향 그래프(Undirected-graph)라고 한다. 각각의 Edge에는 가중치가 붙을 수도 있다.
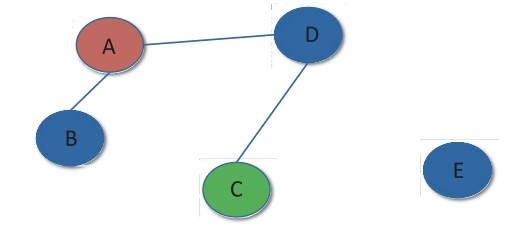
이러한 그래프는 여러 가지를 표현할 수 있다.
- 서울과 부산 간 철도 레일(Node: 서울 & 부산, Edge: 철도)
- 제약 연구(한 분자 내의 원자들이 어떻게 연결되어 있는가)
- 가족 관계(부모와 자식의 연결 관계)
이외에도 인터넷 네트워크, 금융, 정치, 범죄, 심지어는 소설에서 등장인물 간의 관계를 표현하는 것에도 사용될 수 있다.
그럼 그래프로 나타내는 것이 왜 좋을까? 그래프는 다음과 같은 일을 할 수 있다.
- Node간 경로 존재 여부 찾기
- 최단 경로 찾기
- Node 분할하기 (서로 연결된 요소끼리 분리)
- 최소 컷, 최대 유량 문제 (강하게 연결된 요소끼리 분리)
그렇다. 네비게이션으로 최단경로를 찾을 때도 그래프를 활용할 수 있는 것이다!
최초로 그래프를 이용한 사례는 매우 유명한 ‘쾨니히스베르크 다리 문제’이다.
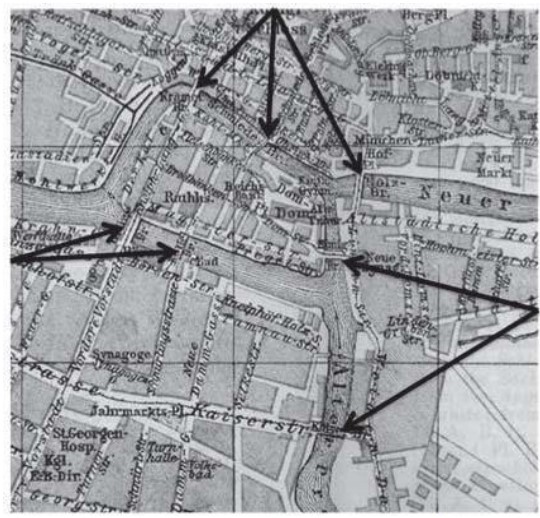
7개의 다리를 딱 한 번만 걸어서 모두 횡단할 수 있을까?
오일러가 내놓은 답은 ‘없다’이다. 오일러는 지도를 그래프로 추상화하여 문제를 해결하였다. 그리고 그 과정에서 ‘다리의 길이’, ‘섬의 크기’와 같은 불필요한 요소는 배제하였다.
그래프는 코드로 구현할 수 있다. 먼저 무향 그래프를 구현하고, 이를 상속(inheritance)받아 유향 그래프를 구현할 수 있다.
그래프 최적화 문제
앞서 언급한 네비게이션처럼, 노드 사이를 이동하는 최단 경로를 그래프로 구할 수 있다.
코드도 코드지만, 코딩에 사용되는 알고리즘을 이해하는 것이 더 중요하다!!
깊이 우선 탐색(DFS)
첫번째 알고리즘은 깊이 우선 탐색(Depth-First Search) 이다. 방법은 다음과 같다.
- 시작점에서 시작
- 특정점(시작점)에서 나가는 모든 Edge를 생각.
- 그 중 하나의 Edge로 이동해서 도착점인지 확인.
- 아니라면, 그 곳에서 2번 과정을 반복.
- 도착점을 찾거나, 선택할 Edge가 없어질 때까지 반복. 선택할 Edge가 없으면 이전 Node로 돌아가서 다음 Edge에 대해 반복.
즉, 하나의 Edge를 선택했으면, 그 길로 끝장을 볼 때까지 다른 Edge는 쳐다도 보지 않는다.
파이썬에서는 이를 재귀함수를 이용해 구현할 수 있다.
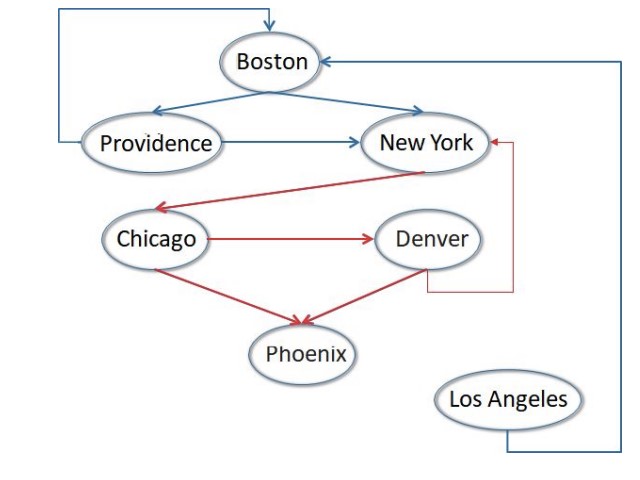
너비 우선 탐색(BFS)
그 다음은 너비 우선 탐색(Breadth First Search) 이다. 방법은 다음과 같다.
- 시작점에서 시작
- 특정점(시작점)에서 나가는 모든 Edge를 생각.
- 그 중 하나의 Edge로 이동해서 도착점인지 확인.
- 아니라면, 시작점으로 돌아와서 다른 Edge를 확인.
- 4에서 도착점을 못 찾으면 시작점에서 거리가 같은 다음 Node로 가서 과정을 반복.
너비 우선 탐색에서 중요한 것은 하나의 level(출발점에서 거리가 같은 모든 Node)을 모두 확인하기 전까지는 다음 level로 넘어가지 않는다는 것이다.
깊이 우선 탐색과는 다르게 너비 우선 탐색은 Edge에 가중치가 있는 경우를 구현하기 힘들다는 단점이 있다.
포스트에 사용된 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기