탐색 트리 구현
지난 강의의 칼로리 문제를 이용해 탐색 트리를 알아보자.
탐색 트리는 맨 위가 뿌리(root)로, 위에서 시작하여 아래로 내려온다.
선택하는 경우는 왼쪽으로, 선택하지 않는 경우는 오른쪽으로 내려간다.
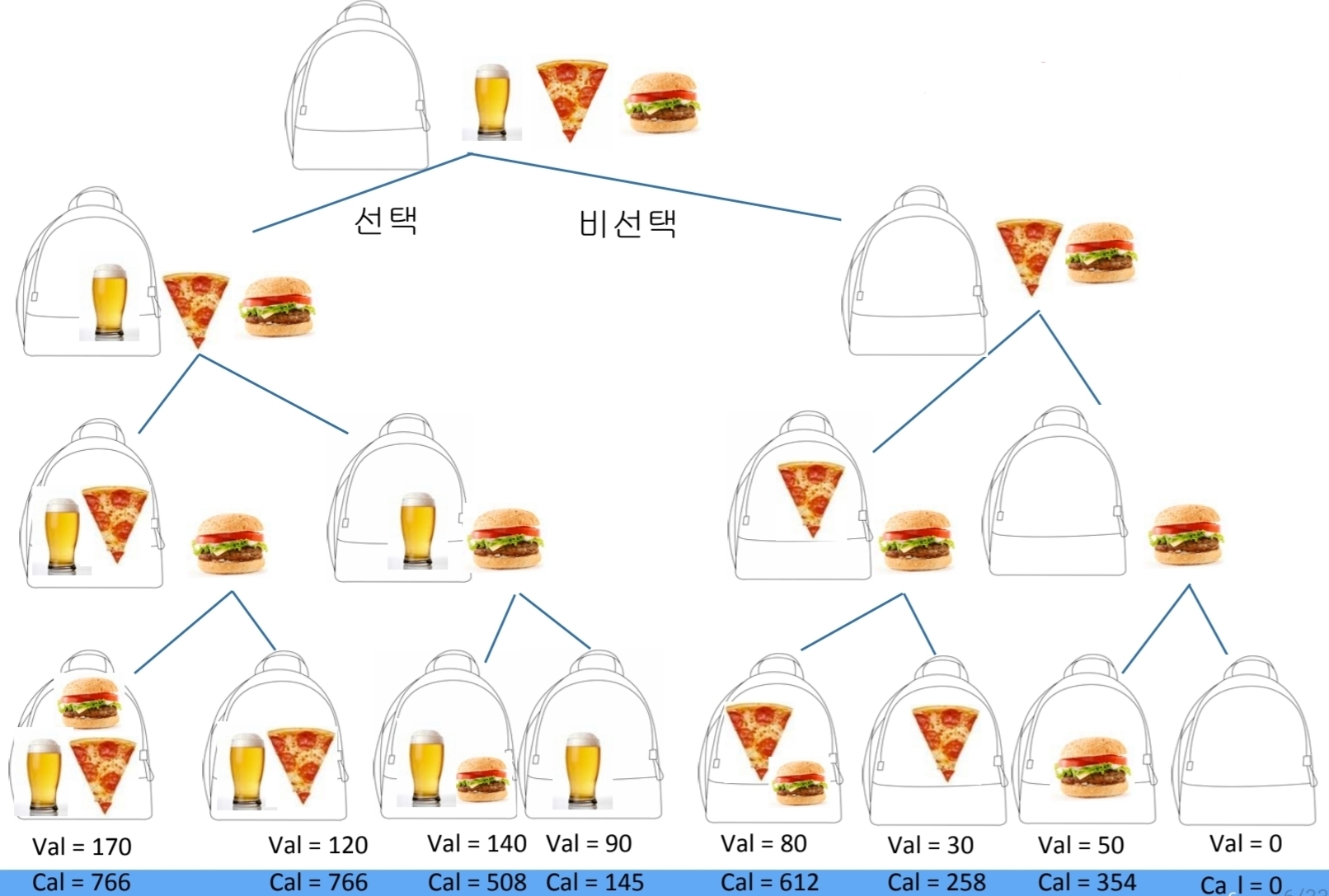
재귀적으로 적용하여 모든 경우를 나타낼 수 있게 된다.
나무의 뿌리가 왜 위에 있냐며 프로그래머가 산책을 안하는 거 같다는 농담은 덤
탐색 트리의 각종 특징을 살펴보자면
- 시간은 만들어진 노드의 개수와 연관
- 레벨의 수는 선택할 수 있는 물건의 수
-
n개의 물건이 있을 때 노드의 수는
-> $\displaystyle \sum_{i=0}^{n}$ $2^i$ = $2^{n+1}$ - 제한 조건을 어기는 트리는 탐색하지 않음
이를 이용해 코드를 만들고 지난 예제에 적용하면 매우 잘 작동한다. 지난 예제의 메뉴가 고작 8개이기 때문이다.
그러나 random 패키지를 이용해 메뉴의 수를 늘리면 점점 시간이 오래 소요된다.
이를 이론적으로 해결하는 방법은 없다. 실생활에서는 동적 프로그래밍으로 해결할 수 있다.
동적 프로그래밍
동적 프로그래밍(Dynamic Programming)이 왜 ‘동적’인지 한동안 궁금하였다.
답은 ‘아무 이유 없다’였다.
파이썬 재귀함수 예시 중 가장 널리 알려진 것이 ‘피보나치’ 문제일 것이다. 아래는 피보나치 재귀함수 코드가 어떻게 동작하는지를 나타내는 그림이다.
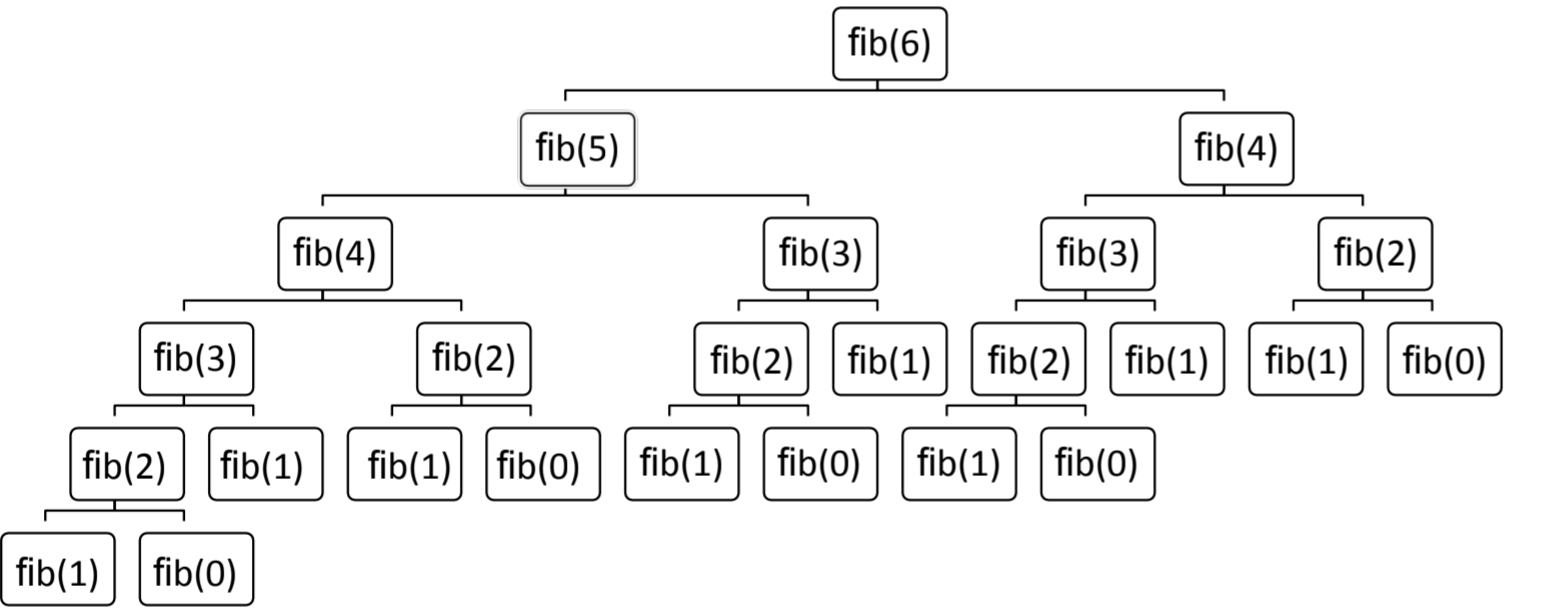
정말 비효율적이다. 왜? 같은 값을 계속 새롭게 계산해야 하니까. 그럼 해결책은?
저장해서 필요할 때 꺼내 쓰자
교수님은 이를 ‘시간과 공간을 맞바꾼다’고 표현한다. fib(x)를 계산하기 전에, 테이블(딕셔너리)을 확인하고 저장된 값이 있다는 이를 불러오는 것이다. memoization이라고도 한다.
최적 부분 구조와 중복 부분 문제
위에서 얻은 insight를 용어로 정리한 것이다.
- 최적 부분 구조: 전역 최적 해를 지역 부분 문제에서 최적 해를 결합함으로써 얻을 수 있는 문제.
- 중복 부분 문제: 최적 해를 구할 때 같은 문제를 여러 번 풀어야 하는 문제
이를 칼로리 냅색 문제에 적용해보자.
- 최적 부분 구조: O
- 중복 부분 문제: X (똑같은 계산을 반복하는 부분이 없다.)
그러나 맥주가 2개(두 종류) 있다고 가정한다면 중복 부분 문제로 볼 수도 있다.
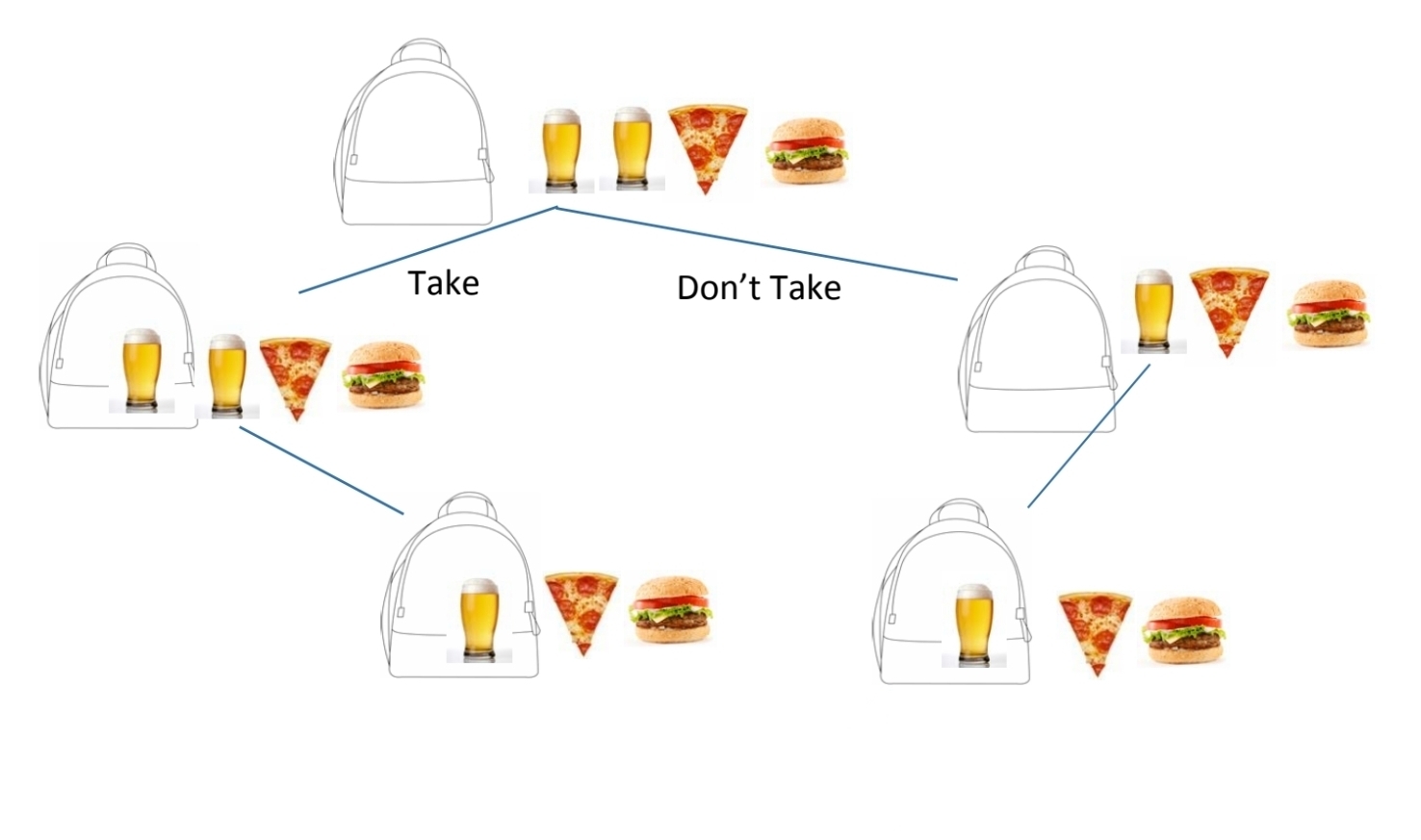
각 노드의 상황을 <선택한 것, 남은 것, 값, 남은 칼로리>로 보았을 때, 실질적으로 선택에서 고려되는 것은 ‘남은 것’과 ‘남은 칼로리’이다.
즉, 남은 칼로리 여유분을 고려하여 남은 물건 중 최대의 가치를 가진 물건을 선택하는 것이다. 이미 무엇을 선택했는지는 전혀 중요하지 않다.
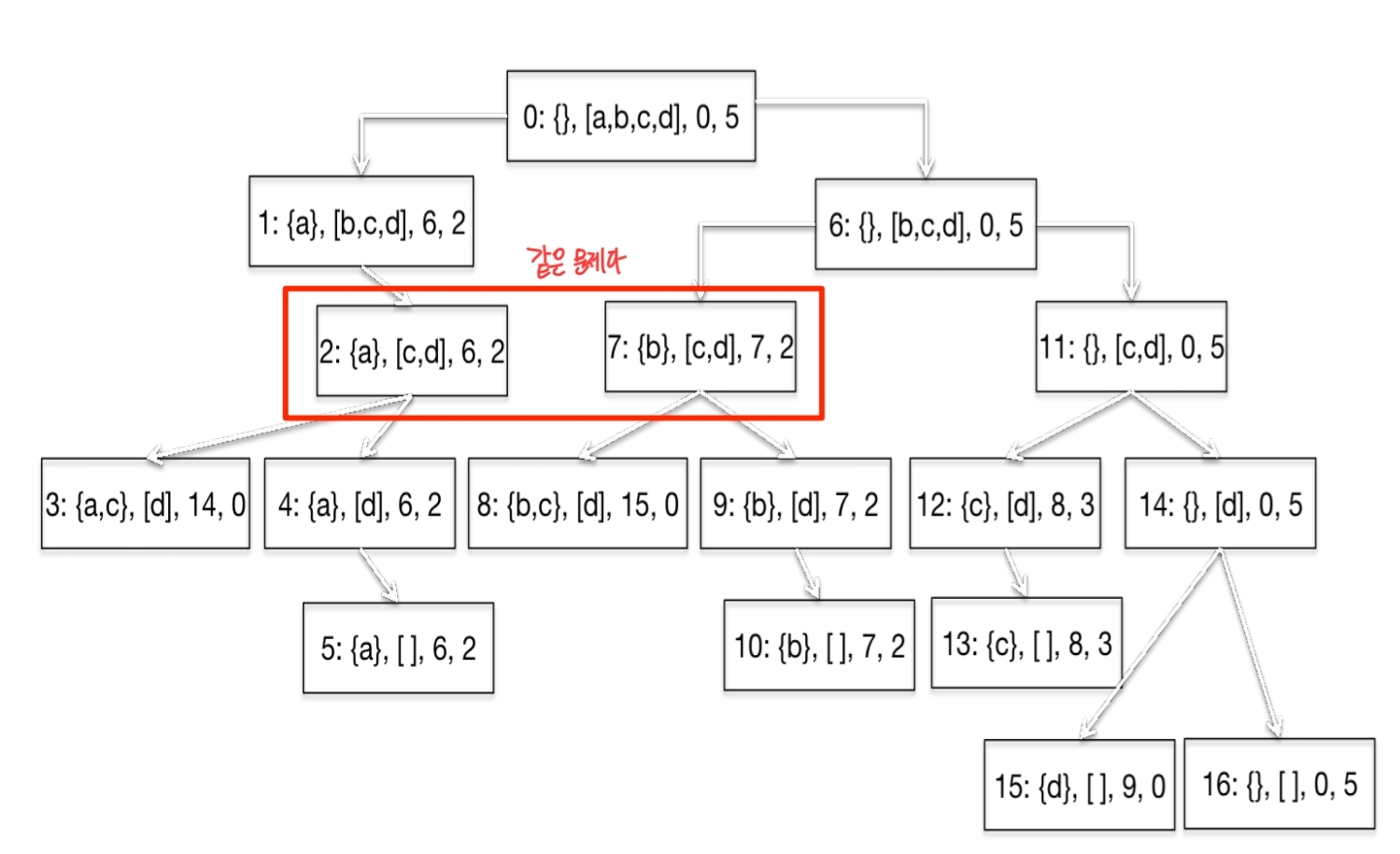
앞선 코드들에 남은 물건을 나타내는 memo 인수를 추가하여 최종적인 알고리즘을 만들 수 있다.
그리고 이는 단순한 재귀 함수 코드보다 매우매우매우매우 효율적이다.
최적 부분 구조와 중복 부분 문제를 가지는 경우 동적 프로그래밍은 매우 좋다!
포스트에 사용된 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기