통계의 함정(지난 강에 이어서)
y축의 스케일을 조작하여 혼란을 주는 것은 문제가 되지만, 필요할 경우에는 적절히 y축을 조절해야 할 떄도 있다.
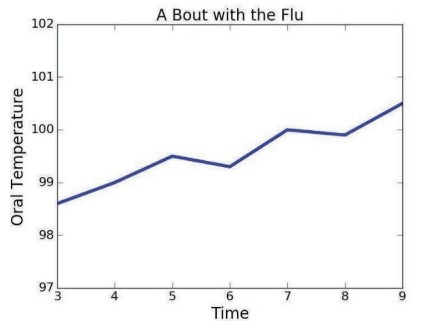
인간의 체온이 0도일 수는 없다. 불필요한 y축은 데이터를 들여다보는 데 방해가 되기도 한다.
적절한 간격을 설정하는 것도 중요하다. 다음은 온난화 데이터에 대한 두 가지 그래프이다.
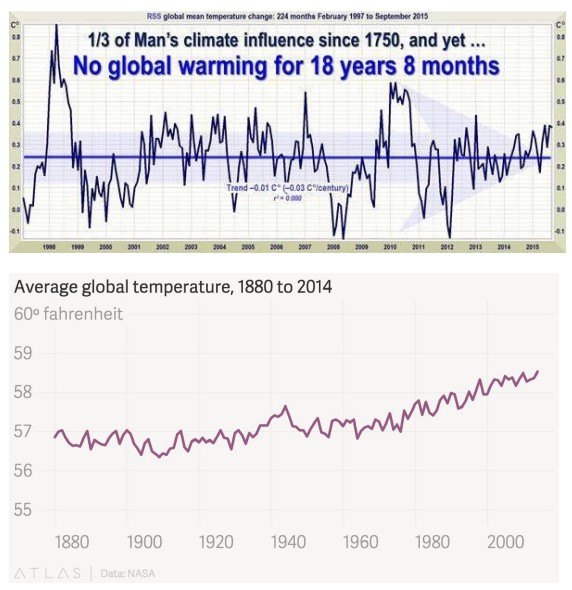
위 아래의 가장 큰 차이점은 시간의 간격이다. 위 그래프는 겨우 18년의 데이터를 나타내고 있다. 당연히 여름에는 기온이 올라가고 겨울에는 기온이 하강한다. 변동과 경향을 혼동해서는 안되며, 적절한 간격을 설정해 제대로 된 경향을 파악할 수 있도록 해야한다.
‘체리피킹’ 역시 경계해야 한다. 잘 익은 체리만을 나무에서 따는 것처럼 원하는 결론을 지지하는 데이터만을 선별해서 분석한다는 뜻이다. 대부분의 과학적 논문이 체리피킹 오류를 범하고 있으며, 그들과 동일한 데이터로 전혀 상반되는 결론을 도출할 수도 있다는 문제점을 가지고 있다.
숫자는 항상 상대적이다. 우리는 간혹 ‘A 동물의 유전자 염기서열이 B동물의 것과 99.9% 일치한다’라는 말을 종종 마주친다. 염기서열에 별 차이가 없는 것처럼 보이지만, 생명체의 염기서열은 매우 많다. 인간만 해도 유전자가 4만개가 있으며, 그 유전자를 구성하는(혹은 구성하지 않는) 염기서열은 셀 수 없다. 그 수의 0.1%는 실로 어마어마한 차이일 수 있는 것이다.
다른 예시에서도 숫자의 함정을 볼 수 있다. 월급이 1억에서 4억으로 오르는 것과, 1달러달라에서 4달러로 오르는 것은 다르다. 둘 다 2배가 오르는 것이지만, 우리는 전자가 후자보다 더 좋다고 생각한다.
다중 가설 실험과 해결
교수님은 하나의 실험을 진행한다.
10,000평방 마일의 지역에 매년 36,000개의 암이 발생한다. 주지사는 이곳을 10평방 마일의 지역 1000개로 나누어 분석하기로 결정했다. 그는 지역별로 36개의 암이 발생할 것으로 예측했다. 그리고 그는 111번 지역에서 지난 3년간 143건의 암 발생이 있었던 것을 발견하였다.
그럼 우리는 111번 지역이 무언가 유해한 물질이 있어서 그 지역에 암 발병률이 높았다고 생각할 수 있다. 그런데, 과연 그럴까?
결과를 보면, ‘111번 지역에서 3년간 143명 이상의 환자가 나올 확률’은 0.1정도이다. 그런데, ‘어느 한 지역에서 3년간 143명 이상의 환자가 나올 확률’을 계산하면 0.6 정도이다. 즉, 111번 지역은 그냥 다른 지역보다 좀 더 불운해서 암환자가 많이 나온 것이지, 그 지역에 무슨 특이한 문제가 있어서가 아니다.
무슨 말장난 같을 수도 있다. 이 예시를 쉽게 바꾸면 더 이해가 잘 될 것이다.
‘내가 복권에 당첨될 확률은 매우 낮지만, 매 회차마다 당첨되는 사람은 반드시 나온다.’
우리는 후자에 기대를 걸고 복권을 구매한다.
암환자 예시처럼, 1000개의 다중 가설을 세우고 가장 마음에 드는 하나를 고르는 것은 부적절하다. 우리가 뒤이어 해결한 것처럼, ‘본페로니 검정’ 등을 이용해야 한다.
더 자세한 것은 통계학 수업을 들어봐야 할 것 같다…

댓글남기기