강의 앞 부분에서는 지난 강의 내용을 마무리하였다.
로지스틱 회귀 (지난 강에 이어서)
지난 시간에 사용한 타이타닉 예시로 k-최근접 분류(KNN)와 로지스틱 회귀의 성능 비교를 할 수 있다.
성능 자체에는 큰 차이가 없으나, 로지스틱 회귀가 조금 더 낫다.
로지스틱 회귀가 제공하는 가중치는 그 자체로는 의미가 없다. 반드시 다른 특성의 가중치와 비교하여 상대적인 해석을 해야 한다.
로지스틱 회귀에는 L1 회귀와 L2회귀가 있다. L1회귀는 한 변수를 0으로 만드는 방식으로, 과대적합을 방지할 수 있다는 장점이 있다. 그러나 서로 상관관계가 있는 변수 중 한 가지를 0으로 만들면 지나친 일반화를 할 수 있다는 단점도 존재한다. L2(default) 회귀는 변수들 간 가중치를 분배하는 방식이다.
상관 특성의 영향을 파악하고 싶다면 특성 하나를 제거하고 실험해보면 된다. (Loss-of-function처럼) 든 자리보다는 난 자리가 더 티가 나는 법이다.
Cutoff를 변경하여 원하는 방식의 결과를 얻을 수도 있다. 생존 확률이 0.5가 아닌 0.9보다 클 떄를 생존한다고 분류하면, 민감도(실제 생존자 중 생존자를 구조하는 비율)는 감소하겠으나 특정성(실제 사망자 중 구조되지 않은 비율)을 높일 수 있다.
마지막으로 Receiver Operating Characteristic(ROC)를 살펴보았다. ROC는 cutoff를 변화시켜가면서 특정성과 민감도의 변화를 계산해 그래프로 나타낸 것을 말한다. x축에는 (1-특정성), y축에는 민감도를 배치한다.
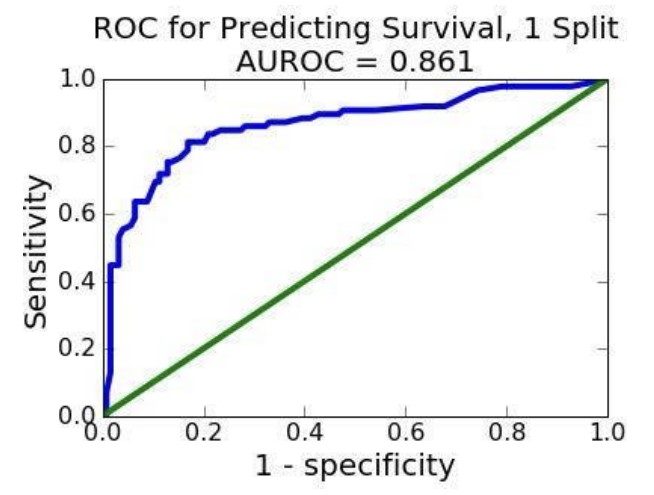
파란색이 ROC 곡선이다. 왼쪽 맨 아래는 민감도 0, 특이도 1인 지점이고, 오른쪽 맨 위는 민감도 1, 특이도 0인 지점이다. ROC 곡선 중간 어딘가를 잘 선정해서 모델에 사용할 수 있다. 그 지점을 계산할 때는 AUROC(Area Under ROC) 개념을 사용한다. 곡선 아래 넓이가 가장 넓은 지점이 가장 적합하다는 의미이다. 녹색선은 random classifier를 나타낸다. 즉, 녹색선보다 아래에 있다는 것은 모델이 랜덤한 것만 못하다는 뜻이며, 녹색선 위에 있어야 통계적으로 유의미한 것이다.
통계의 함정
거짓말에는 세 가지 종류가 있다.
- 거짓말
- 빌어먹을 거짓말
- 통계
통계를 교묘하게 사용하여 사람들을 현혹시키거나 교란하는 행위는 예전부터 많이 존재해왔다. y축의 스케일을 조작하여 실제보다 격차가 커보이게 하거나 작아보이게 하는 것은 너무 뻔한 수법이라 (순식간에 지나가지 않는 한) 속는 사람이 많지 않다.
또다른 수법으로는 집단을 조작하는 것이다. 왠지 점점 조작 방법 소개가 되는 것 같다 아래 그래프는 복지기금을 수령하는 미국인들의 수를 나타낸 것이다.
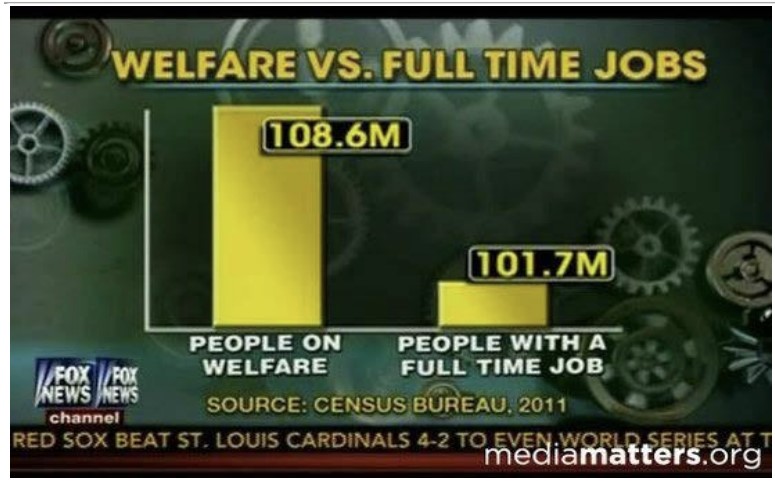
복지연금을 수령하는 사람이 그렇지 않은 사람보다 훨씬 많아 보인다(y축 스케일 조작은 단골손님이다). 그러나 이 숫자가 도출된 방법이 참으로 기가 막힌다. 복지연금을 수령하는 사람은 부모 중 한 사람만 받아도 ‘가족 전체’를 포함시킨 숫자이다. 반면, 고용된 사람은 ‘그 사람만’ 포함하는 숫자이다.
앞선 강의에서 살펴본 선형회귀도 맹점이 있다. 아래 데이터는 ‘앤스콤 4분할 그래프’라고 불리는 예시이다.
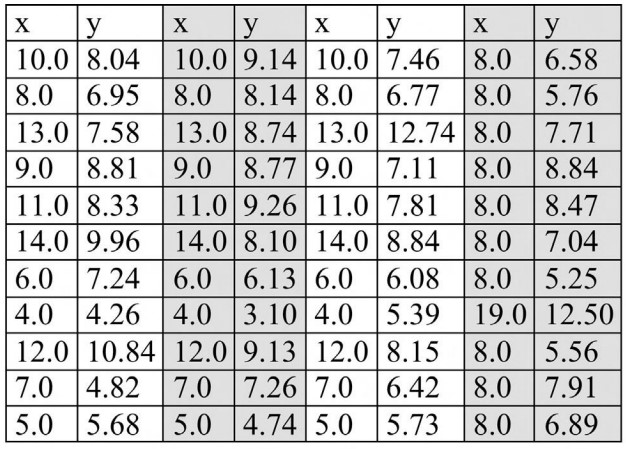
이 표의 네 부분은 모두 동일한 평균, 분산, 선형회귀 모델($y = 0.5x + 3$)을 가진다. 그럼 유사한 데이터셋일까?

전혀 다른 모습을 한 데이터들이다.
통계로 장난치는 몇 가지 방법을 살펴보았다. 여기서 우리는 이런 교훈을 얻을 수 있다.
- 데이터의 통계 $\neq$ 데이터 그 자체
- 데이터를 직접 plot해봐야 한다.
- 축의 레이블과 스케일을 봐야한다.
- 서로 비교가 가능한 집단인지 살펴본다.
Garbage In Garbage Out
“쓰레기가 들어가면 쓰레기가 나온다. Garbage In Garbage Out(GIGO)”
시뮬레이션 모델 제작에서 가장 유명한 격언 중 하나이다. 아무리 훌륭한 시뮬레이션 모델을 만들더라도 모델에 투입하는 데이터가 엉망이면 좋은 결과가 나올 수 없다는 것이다.
과거 한 때는 측정 오류가 편향되어있지 않고 서로 독립적이어서 오류들이 균형을 맞출 수 있다고(마치 상쇄하듯이) 생각했다. 다시 말하면 쓰레기가 들어가도 좋은 결과물이 나올 수 있다는 말이다. 그러나 오류가 무작위가 아닌 계통적이라는 것을 알게된 뒤에는 불량데이터가 매우 위험하다는 사실을 깨닫게 되었다.
샘플링
GIGO를 유발할 수 있는 가장 취약한 부분은 샘플링이다. 모든 통계학적 기술은 집단의 부분을 샘플링하여 전체 집단에 대한 정보를 유추할 수 있다고 가정한다. 그리고 그 샘플은 무작위적 추출에 의해 형성된다.
이 가정은 적어도 앞서 제작한 파이썬 코드에서는 성립한다. 그러나 현실은 다르다.
발생할 수 있는 한 가지 편향은 생존 편향이다. 제2차 세계대전 당시 연합군의 전투기가 독일의 대공포에 공격을 받고 격추되거나 심하게 파손된 채로 복귀하자, 이를 보완할 방법을 찾기 위해 복귀한 비행기에서 파손된 부분을 보강하였다는 설에서 유래한 용어이다. 매우 어리석은 방법이 아닐 수 없는데, 격추된 비행기를 조사해야 대공포에 치명적인 부분을 발견할 수 있을 것이기 때문이다.
일상에서도 이러한 예시를 찾아볼 수 있다. 학기말에 수강하고 있는 학생을 대상으로 강의평가를 하는 경우가 있다. 그 수업을 매우 싫어하는 학생이나 성적을 잘 못받을 것 같은 학생이 이미 드랍했을 것이므로, 별로 도움이 안되는 설문 결과라고 할 수 있다.
다른 편향은 ‘비응답 편향’이다. 간혹 식당이나 호텔을 방문하면 고객이 원하는 경우 만족도 설문을 할 수 있게 설문지를 제공한다. 대부분의 사람들은 설문을 잘 하지 않는다. 매우 만족하거나 매우 불만족할 경우(불만족할 경우 설문을 할 정신이 있을지는 모르겠다만) 설문을 할 것이다. 따라서 그리 유용한 결과라고는 할 수 없다.
데이터가 어떻게 수집되었는지를 파악하는 것은 매우 중요하다. 통계학적으로 설정된 가정을 제대로 만족하는 수집 방법인지 판단하고, 그렇지 않을 경우 그 결과에 대해 신뢰해서는 안된다. (악용해서는 더더욱 안된다.)
포스트에 사용된 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기