머신러닝
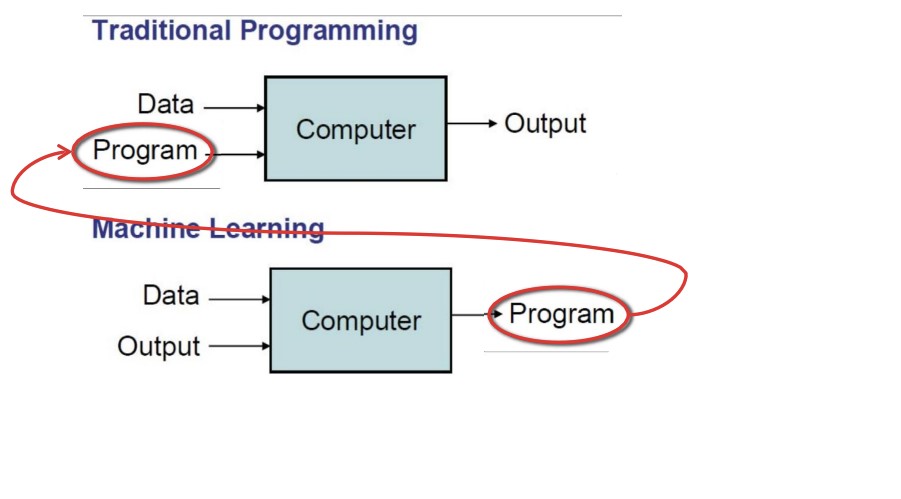
머신러닝은 컴퓨터가 스스로 학습하게 하는 것을 의미한다. 프로그래머가 코딩으로 프로그램을 만들고 데이터를 입력해 결과를 내는 것이 전통적인 프로그래밍이었다면, 다양한 데이터와 정답(결과)을 컴퓨터에게 주고 이를 이용해 프로그램을 만들어 내는 것이 머신러닝인 것이다.
학습의 방법에는 두 가지가 있다. 많은 정보를 기억하는 ‘선언적 지식’과 이전의 사실로부터 일반화를 통해 새로운 사실을 유추하는 ‘절차적 지식’이다. 컴퓨터에 단순히 많은 양의 정보를 저장하는 것을 넘어, 머신러닝은 이제 절차적 지식의 단계에 도달해있다.
지도학습과 비지도학습
기본적인 머신러닝의 패러다임에서 나아가, 머신러닝은 크게 두 가지로 나뉜다.
- 지도학습: 특성 & 레이블 쌍의 집단을 가지고 새로운 입력값에 대한 레이블을 예측하는 규칙을 찾는 것
- 비지도학습: 특성벡터(레이블 없음)를 가지고 집단에 대한 레이블을 형성하거나 클러스터링(그룹화)하는 것
비지도학습은 레이블을 제공하지 않기 때문에 ‘비’가 붙었다. 쉽게 말해, ‘입력값이 어디에 속해?’를 묻는다면 지도학습, ‘비슷한 것끼리 구분해봐’를 시킨다면 비지도학습으로 볼 수 있다.
비지도학습 예시
교수님은 미식축구 선수들의 신장과 몸무게 데이터를 예시로 설명을 진행한다. 포지션에 대한 정보가 없는(레이블이 없는) 데이터를 나타내면 아래와 같다.
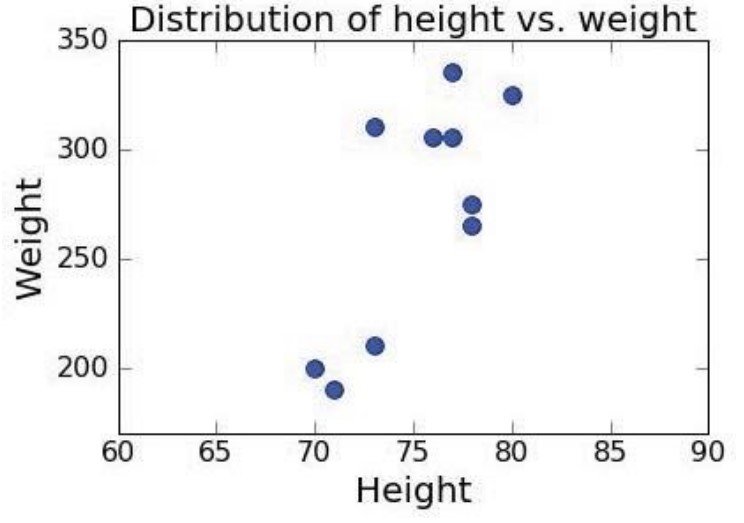
클러스터링을 하고 싶다면 ‘거리 측정’을 사용하면 된다.
- k개의 집단을 만들고 싶다면 k개의 샘플을 대표값으로 설정한다.
- 남은 것들을 대표값들과의 거리를 재서 가장 가까운 샘플에 넣는다.
- 집단의 중간값을 새로운 대표값으로 설정한다.
- 변화가 생기지 않을 때까지 반복한다.
미식축구 데이터로 클러스터링을 하면 다음과 같다.
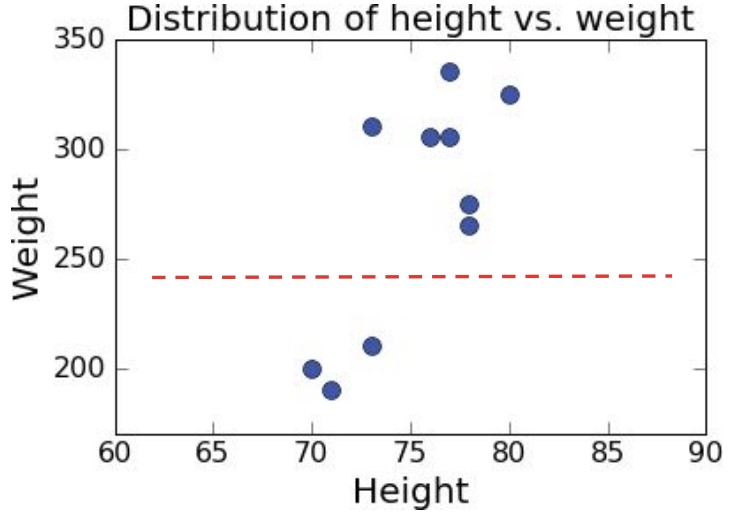
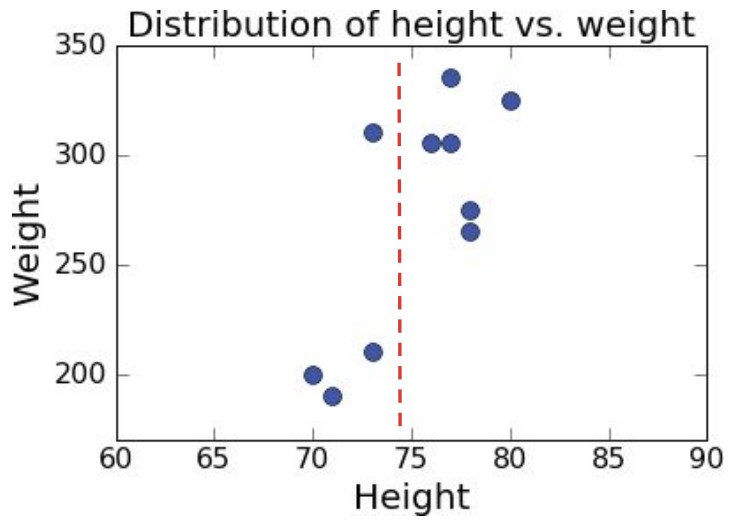
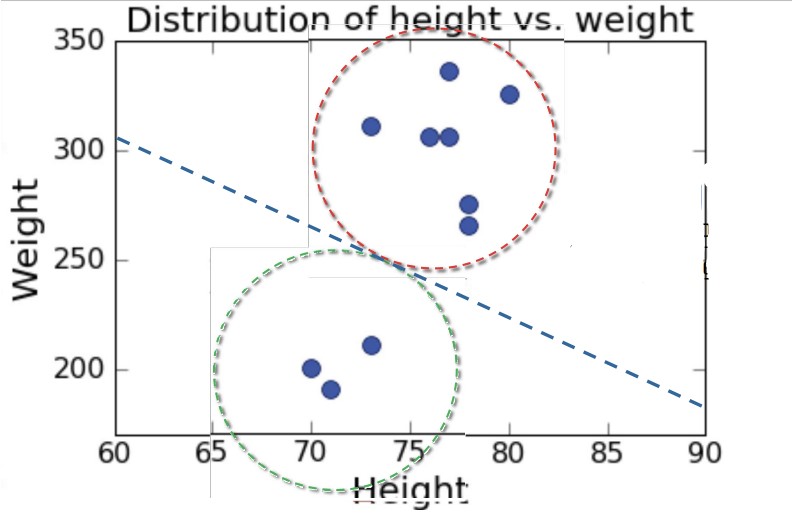
지도학습 예시
이번엔 레이블이 있는 데이터로 해보자. 미식축구 선수 데이터에서 레이블은 포지션에 해당한다.
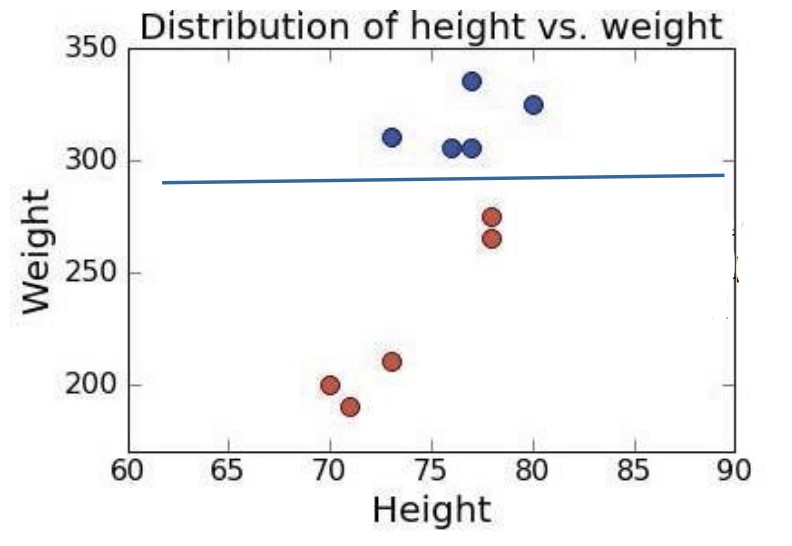
레이블 있는 데이터는 이렇게 나누어진다.
새로운 포지션을 가진 선수 데이터가 추가되었다고 해보자. 이 경우 처음에 레이블이 있었을 떄와 없었을 떄 클러스터링 상황이 달라지게 된다.
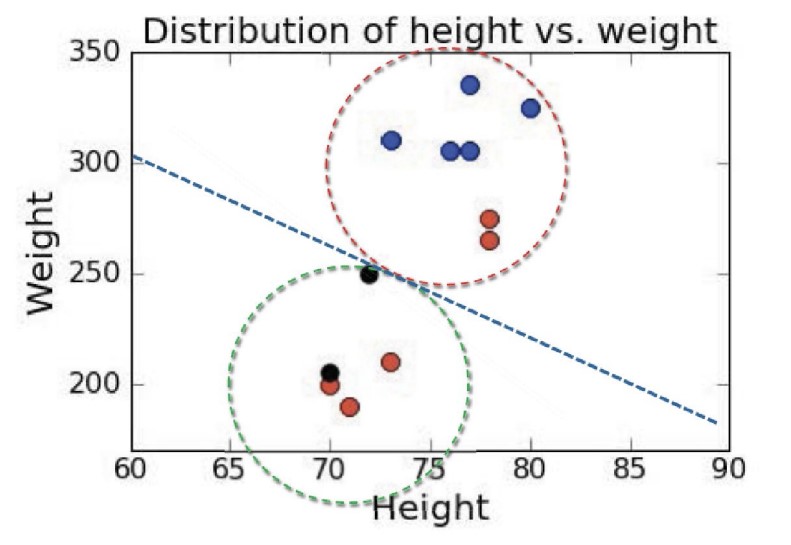
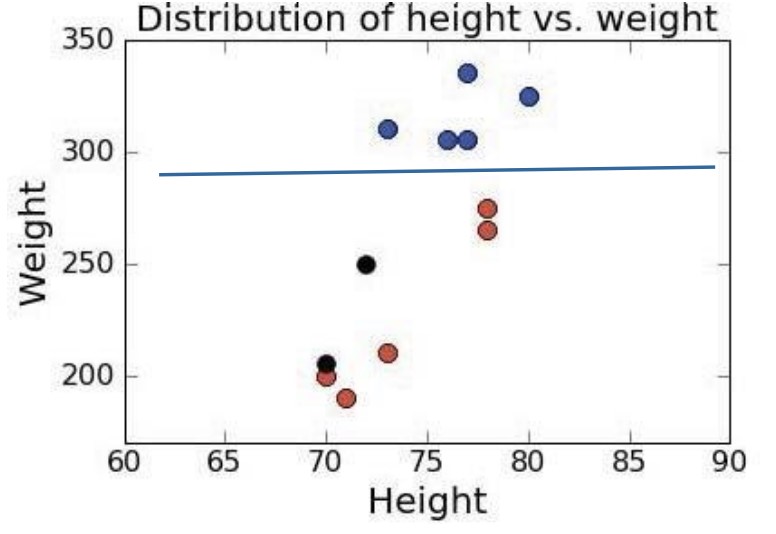
머신러닝에서 클러스터링을 할 떄 확실하게 알아야 할 것이 있다. ‘과대적합’ 없이 집단을 완벽하게 구분하기는 어렵다는 것, ‘긍정 오류’와 ‘부정 오류’를 비용으로 생각해야 한다는 것이다.
특성 표시 방식
클러스터링에서는 다양한 특성을 사용할 수 있다. 보통 일반화하기 편하도록 특성 벡터로 나타낸다. 클러스터링에 유용하게 사용할 수 있는 특성도 있겠지만, 그렇지 않은 특성도 많다.
예를 들어, 대학교 학점을 학생의 특성에 따라 부여한다고 생각해보자. 신입생 시험 점수, 과거의 전공 학점 등은 성적을 부여하는 데 꽤 유용하게 사용할 수 있을 것이다. 그러나 학생의 출신 지역, 몸무게 등은 별 도움이 되지 않는 특성일 것이다. 유용한 입력과 그렇지 않은 것을 구별하는 것은 중요하다.
여기서도 (세상의 모든 것이 그러하듯) 완벽할 수는 없다. 신입생 시험은 열심히 보고 대학생활은 불성실하게 하는 학생이 있을 수 있고, 다른 과목 실력은 좋지만 해당 과목 실력은 현저하게 떨어지는 학생도 있을 수 있다. 그러나 이러한 오류는 모두 감수해야 한다. 긍정오류(A를 주면 안되는 학생에 A 부여)과 부정오류(A를 줘야 하는 학생에 A를 주지 않음) 중 어느 것을 더 줄일 것인지는 본인의 선택이다.
특성 간의 거리 재기
특성을 벡터로 나타냈다면 데이터들이 가진 특성 벡터 간의 거리를 재야할 것이다. 두 가지 방법이 있다.
- 맨해턴 거리
- 유클리드 거리
맨해턴 거리는 미국의 도로처럼 가로와 세로만으로 이루어진 격자에서의 거리를 의미한다. 대각선으로 가로질러 갈 수 없고, 반드시 가로와 세로의 거리를 더해야 한다.
유클리드 거리는 익숙하다. x좌표는 x끼리, y좌표는 y끼리 차를 구하고 제곱해서 더한 뒤 제곱근을 구하면 된다. 식으로 나타내면 다음과 같다.
\[\displaystyle dist(X1, X2, p) = (\sum_{k=1}^{len}{abs(X1_k-X2_k)^p})^{1/p}\]p = 1: 맨해턴 거리
p = 2: 유클리드 거리
보통은 유클리드 거리를 많이 사용한다. 그러나 특정한 특성이 다른 특성과는 다른 스케일을 가질 경우(ex. 동물의 다리 개수), 유클리드 거리를 사용하면 해당 특성이 다른 특성보다 부각될 수 있다 (마치 가중치가 가해진 것처럼). 이 때는 맨해턴 거리를 사용해야 한다.
민감도와 특정성
머신러닝 모델의 정확도는 다음처럼 구한다.
\[정확도 = \frac{true\,positive\,+\,true\,negative}{true\,positive\,+\,true\,negative\,+\,false\,positive\,+\,false\,negative}\]진단검사 그거 맞다
전체 중에 올바르게 분리된 것의 비율을 구하면 된다.
다만, 정확도가 동일한 모델 중에 내가 더 필요로하는 모델을 고를 때는 조금 다른 수치를 사용해야 한다.
민감도는 올바르게 찾은 비율을 의미한다. 풀어서 쓰면, ‘A라고 분리한 데이터 중에 진짜 A인 데이터’의 비율인 것이다.
\[민감도 = \frac{true\,positive}{true\,positive\,+\,false\,negative}\]다른 값으로는 특정성도 있다. ‘A가 아니라고 분리한 데이터 중에 진짜로 A가 아닌 데이터’의 비율을 가리킨다.
\[특정성 = \frac{true\,negative}{true\,negative\,+\,false\,positive}\]
포스트에 사용된 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기