HJ

Leave HJ’s trace, All-In

비지도 학습

비지도 학습(Unsupervised Learning)은 레이블이 없는 데이터로 하는 학습을 말한다. 다음은 비지도 학습의 예시이다.

  1. 군집
  2. 이상치 탐지
  3. 밀도 추정: 데이터셋의 확률 밀도 함수를 추정하여 이상치 탐지에 사용.


군집

비슷한 샘플을 하나의 군집(cluster)로 할당하는 작업을 군집화(clustering)라고 한다. 다음과 같은 곳에 활용할 수 있다.

  1. 고객 분류
  2. 데이터 분석: 새로운 데이터셋을 분석할 때 비슷한 군집끼리 모아서 따로 분석.
  3. 차원 축소 기법
  4. 특성 공학
  5. 이상치 탐지
  6. 준지도 학습: 일부 데이터만 레이블이 있을 때, 군집을 형성하고 같은 군집에 레이블을 전파.
  7. 검색 엔진
  8. 이미지 분할

Centroid는 군집을 찾기 위한 특정 포인트로, centroid를 중심으로 모인 샘플을 찾아서 군집을 형성한다.


k-means clustering 기초

k-평균은 k개의 군집으로 분류하는 알고리즘이다. 이는 다음과 같이 작동한다.

  1. 랜덤한 k개의 centroid 선정.
  2. 샘플에 레이블 할당하고 centroid 업데이트.
  3. Centroid에 변화가 없을 때까지 2를 반복.

위 알고리즘은 무조건 수렴하지만 항상 전역 최적에 수렴하는 것은 아니다(centroid 랜덤 초기화가 중요하다). 또한, 샘플을 군집에 할당할 때 centroid와의 거리만 고려하므로, 군집의 크기가 다르면 잘 작동하지는 않는다.

샘플의 하나의 cluster에만 할당하는 hard clustering보다, 각 cluster마다 샘플에 점수를 부여하는 soft clustering이 유용할 수 있다. 다음 코드는 hard clustering과 soft clustering을 모두 구현한다.

from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
import numpy as np

blob_centers = np.array([[ 0.2,  2.3], [-1.5 ,  2.3], [-2.8,  1.8],
                         [-2.8,  2.8], [-2.8,  1.3]])
blob_std = np.array([0.4, 0.3, 0.1, 0.1, 0.1])
X, y = make_blobs(n_samples=2000, centers=blob_centers, cluster_std=blob_std,
                  random_state=7)
k = 5
kmeans = KMeans(n_clusters=k, random_state=42)
y_pred = kmeans.fit_predict(X)

kmeans.cluster_centers_     # print centroid

# predict cluster
X_new = np.array([[0, 2], [3, 2], [-3, 3], [-3, 2.5]])

# hard clustering
kmeans.predict(X_new)

# soft clustering - return the distance to each centroid
kmeans.transform(X_new).round(2)

찾은 솔루션이 최선의 솔루션인지를 평가하는 지표로는 inertia가 있다. 이는 각 샘플과 가장 가까운 centroid 사이의 제곱 거리 합이다. 대체로 inertia가 작을수록 좋은 솔루션인 것이다(물론 항상 그런 것은 아니다).

kmeans.inertia_


Centroid 초기화

이미 좋은 centroid를 알고 있다면 다음과 같이 init에 할당하여 훈련할 수도 있다. n_init은 랜덤 초기화 횟수를 의미한다(기본 10).

good_init = np.array([[-3, 3], [-3, 2], [-3, 1], [-1, 2], [0, 2]])
kmeans = KMeans(n_clusters=5, init=good_init, n_init=1, random_state=42)
kmeans.fit(X)

Centroid를 초기화하는 더 나은 방법은 k-평균++ 알고리즘이다. 이는 k-평균 알고리즘이 최적이 아닌 솔루션으로 수렴할 가능성을 크게 낮춘다.

  1. Dataset에서 랜덤으로 균등하게 하나의 centroid $\bf{c^{(1)}}$ 을 선택한다.
  2. $\frac{D(\bf{x^{(i)}})^2}{\displaystyle \sum_{j=1}^{m}{D(\bf{x^{(j)}})^2}}$ 의 확률로 샘플 $\bf{x^{(i)}}$ 를 새로운 centroid $\bf{c^{(i)}}$ 로 선택한다. $D(\bf{x^{(i)}})^2$ 는 $\bf{x^{(i)}}$ 와 이미 선택된 가장 가까운 centroid까지의 거리이다. 즉, 이미 선택한 centroid에서 멀리 떨어진 샘플이 다음 centroid가 될 확률이 높다.
  3. k개의 centroid가 선택될 때까지 2를 반복한다.

KMeans 클래스는 기본적으로 k-평균++ 알고리즘을 사용한다.


k-means 속도 개선

Charles Elkan(2013)은 대규모 dataset에서 삼각 부등식을 활용해서 불필요한 거리 계산을 피하고 알고리즘을 속도를 향상시키는 방법을 제안했다. 그러나 이 알고리즘이 항상 잘 작동하는 것은 아니며, 때로는 오히려 훈련 속도가 느려질 수도 있다.

# Elkan
good_init = np.array([[-3, 3], [-3, 2], [-3, 1], [-1, 2], [0, 2]])
kmeans = KMeans(n_clusters=5, algorithm="elkan", n_init=1, random_state=42)
kmeans.fit(X)

David Sculley(2010)는 k-평균을 알고리즘에서 각 반복마다 하나의 mini-batch만 활용해 centroid를 업데이트 하는 mimi-batch k-평균을 제안했다. 이는 알고리즘의 속도를 3~4배 정도 높인다. 물론, mini-batch를 활용하는 특성 상 inertia는 조금 나쁘다.

# Mini-batch KMeans
from sklearn.cluster import MiniBatchKMeans
minibatch_kmeans = MiniBatchKMeans(n_clusters=5, random_state=42)
minibatch_kmeans.fit(X)


최적의 k 찾기

최적의 cluster 개수 k를 찾는 것은 간단하지 않다. 단순히 inertia가 적으면 된다고 생각할 수도 있지만, cluster가 많아질수록 샘플과 centroid의 거리가 줄어드는 것은 당연하다.

Cluster가 많아질수록 inertia가 줄어들기는 하지만, 그 감소 속도가 눈에 띄게 줄어드는 지점이 있다. 이를 elbow라고 한다. 이 지점을 k의 후보로 놓을 수도 있다.


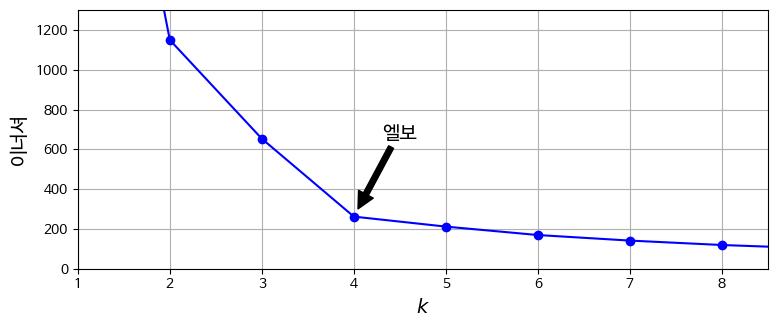
다른 방법은 silhouette score(실루엣 점수)를 활용하는 것이다. 이 값은 모든 샘플에 대한 silhouette coefficient(실루엣 계수)의 평균인데, silhouette coefficient는 다음과 같이 구한다.

\[silhouette \; coefficient = \frac{b - a}{max(a, b)}\]
  • a: 동일한 cluster에 있는 다른 샘플까지의 평균 거리 (cluster 내부 평균 거리)
  • b: 자신이 속한 cluster를 제외한, 가장 가까운 cluster까지의 평균 거리.

Silhouette coefficient의 의미는 다음과 같다.

  • 1에 가깝다 = a가 작고 b가 크다 = 자신의 cluster에 잘 속해있고, 다른 cluster와는 멀리 떨어져 있다.
  • 0에 가깝다 = a와 b가 비슷하다 = cluster 경계에 있다.
  • -1에 가깝다 = a가 크고 b가 작다 = 잘못된 cluster에 할당되어 있다.
# silhouette score
from sklearn.metrics import silhouette_score
silhouette_score(X, kmeans.labels_)

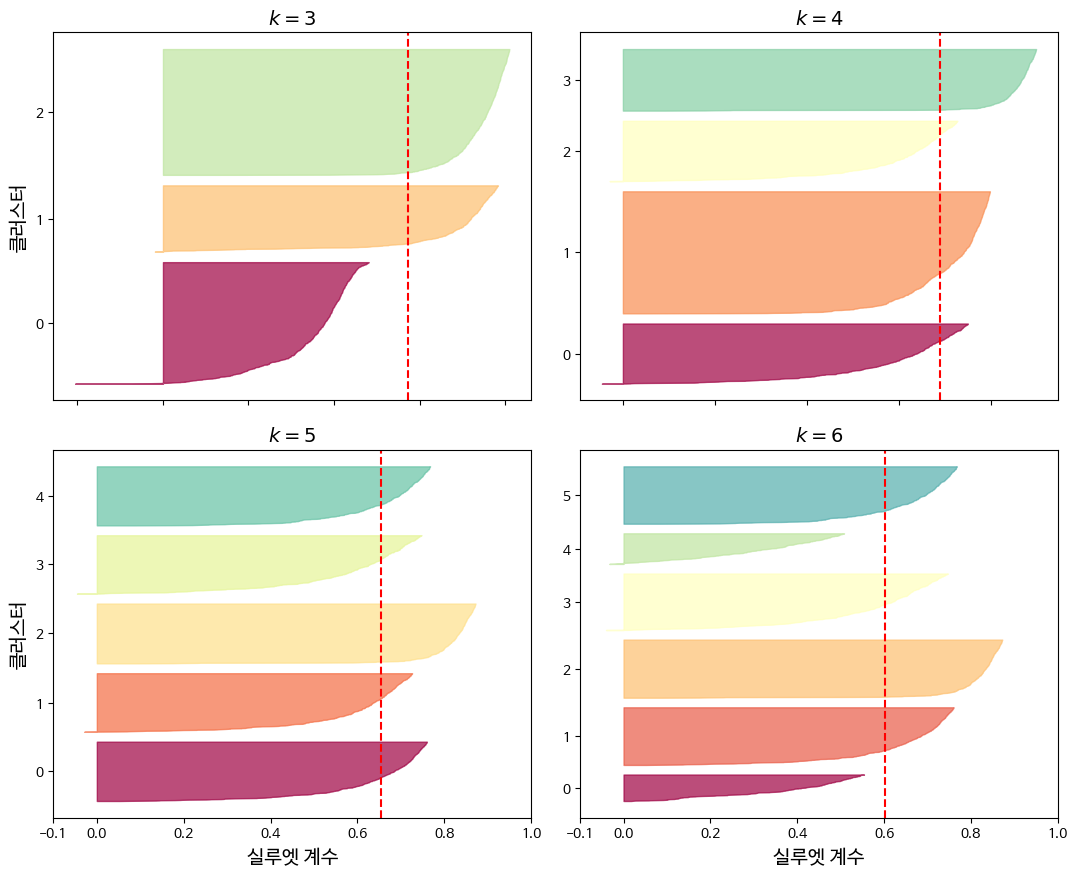
Silhouette diagram을 이용하면 더 많은 정보를 얻을 수 있다. 각 cluster마다 칼 모양의 그래프가 그려지는데, 의미는 다음과 같다.

  • 그래프의 높이: Cluster가 포함하는 샘플의 개수.
  • 그래프의 너비: Cluster에 포함된 샘플의 정렬된 silhouette coefficient. 즉, 넓을수록 좋다.
  • 파선: 각 cluster 개수에 해당하는 평균 silhouette score. 즉, 어느 한 cluster가 이 파선보다 낮으면, 그 cluster의 샘플이 다른 cluster와 너무 가깝다는 뜻.

가장 적절한 silhouette coefficient와 클러스터 크기를 만족하는 k를 고르면 된다(diagram 생성 방법은 코드 참조).



k-means의 한계

k-평균은 장점도 많지만 단점도 있다.

  1. 최적이 아닌 솔루션을 피하려면 여러 번 실행해야 한다.
  2. k를 지정해야 한다.
  3. Cluster의 크기, 밀집도가 다르거나 원형(구형)이 아닐 경우 잘 작동하지 않는다. 타원형의 cluster에서는 엉망으로 작동한다.

그리고 단점이라고 하기엔 무리지만 반드시 데이터를 미리 scaling해야 한다. 분포를 항상 원형으로 만들어주진 않지만 과정에 도움은 될 것이다.

코드 보러가기



별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기

참고