Random Projection
Random Projection은 말 그대로 랜덤한 선형 투영을 사용해서 projection을 한다. 이는 William B.Johnson과 Joram Lindenstrauss의 정리에서 증명되었듯이 실제로 거리를 상당히 잘 보존할 가능성이 매우 높다. 즉, 매우 다른 샘플 두 개는 투영 후에도 매우 다르게 남고, 비슷한 샘플은 비슷하게 남는다. Random projection은 고차원 dataset을 다룰 때 반드시 고려해야 한다.
최적의 차원 수는 어떻게 정할 수 있을까? m이 샘플 수, n이 특성 수라고 할 때, 두 샘플 간의 제곱 거리가 $\epsilon=10\%$ 를 초과하지 않도록 하려면 다음 차원 d로 projection해야 한다.
\[d \geq \frac{4 \log(m)}{(\frac{1}{2} \epsilon^2 - \frac{1}{3} \epsilon^3)}\]단순히 파이썬 코드로 구현하면 다음과 같다.
from sklearn.random_projection import johnson_lindenstrauss_min_dim
m, ε = 5_000, 0.1
d = johnson_lindenstrauss_min_dim(m, eps=ε)
n = 20_000
np.random.seed(42)
P = np.random.randn(d, n) / np.sqrt(d) # random matrix P
X = np.random.randn(m, n) # sample dataset
X_reduced = X @ P.T
위 과정과 완전 동일한 사이킷런 클래스도 있다.
from sklearn.random_projection import GaussianRandomProjection
gaussian_rnd_proj = GaussianRandomProjection(n_components=154, random_state=42)
X_reduced = gaussian_rnd_proj.fit_transform(X)
eps는 $\epsilon$ 을 조절하고 n_components는 차원을 d로 강제한다.
SparseRandomProjection이라는 랜덤 투영 변환기도 있다. 랜덤 행렬이 희소하다는 특징이 있으며, 규모가 크거나 희박한 dataset의 경우에는 이 변환기를 쓰는 것이 더 좋다. 메모리도 훨씬 적게 사용한다.
Locally Linear Embedding(LLE)
지역 선형 임베딩(Locally Linear Embedding, LLE)은 비선형 차원 축소(NonLinear Dimensionality Reduction, NLDR) 기술이다. Projection에 의존하지 않는다. 기본적인 과정은 다음과 같다.
- 각 훈련 샘플이 최근접 이웃에 얼마나 선형적으로 연관되어 있는지를 파악한다.
- 1에서 찾은 국부적인 관계가 가장 잘 보존되는 저차원 표현을 찾는다.
좀 더 풀어서 알아보자.
- 각 훈련 샘플 $\bf{x}^{(i)}$ 에 대해. k개의 최근접 이웃을 찾는다.
- 위 이웃에 대한 선형 함수로 $\bf{x}^{(i)}$ 를 재구성한다. 즉, $\bf{x}^{(i)}$ 와 $\displaystyle \sum_{j=1}^{m}{w_{i, j} \bf{x}^{(i)}}$ 사이의 제곱 거리가 최소가 되는 $w_{i, j}$ 를 찾는다. 만약 $\bf{x}^{(j)}$ 가 $\bf{x}^{(i)}$ 의 k개 이웃 중 하나가 아닐 때는 $w_{i, j}=0$ 이다. 그럼 아래와 같은 최적화 문제가 된다. (W는 $w_{i, j}$ 을 모은 행렬.)
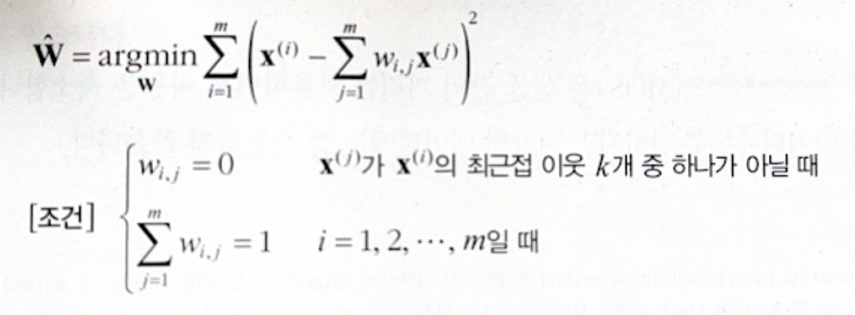
이는 샘플을 고정하고 가중치를 찾는 문제이다. - 가중치 행렬 $\hat{W}$ 는 훈련 샘플 사이의 지역 선형 관계를 담고 있다. 이 관계가 보존되도록 d차원 공간으로 매핑하는 작업을 해야 한다. 즉, $\bf{z}^{(i)}$ 가 d차원에서의 상이라면 $\bf{z}^{(i)}$ 와 $\displaystyle \sum_{j=1}^{m}{w_{i, j} \bf{z}^{(i)}}$ 사이의 거리가 최소가 되어야 한다. 다음과 같은 최적화 문제가 된다.
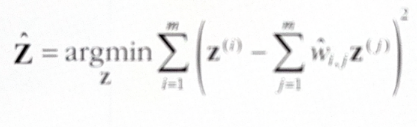
이번에는 앞서와 다르게 가중치를 고정하고 저차원 공간에서 샘플 이미지의 최적 위치를 찾는 것이다.
파이썬 코드를 살펴보자.
from sklearn.datasets import make_swiss_roll
from sklearn.manifold import LocallyLinearEmbedding
X_swiss, t = make_swiss_roll(n_samples=1000, noise=0.2, random_state=42)
lle = LocallyLinearEmbedding(n_components=2, n_neighbors=10, random_state=42)
X_reduced = lle.fit_transform(X_swiss)
아쉽게도, 저차원 표현을 만드는 계산 복잡도가 $O(dm^2)$ 인 관계로 대규모 dataset에 적용하기는 어렵다.
다른 차원 축소 기법
여러가지 다른 차원 축소 기법들이 있다.
- MultiDimensional Scaling(MDS): 샘플 간의 거리를 보존하며 차원 축소. 고차원 dataset에만 적합.
- Isomap: 각 샘플을 가장 가까운 이웃과 연결하고 geodesic distance(두 노드 사이의 최단 경로를 이루는 노드의 수)를 유지하며 차원 축소.
- t-SNE: 비슷한 샘플은 가까이, 비슷하지 않으면 멀리 떨어지도록 차원 축소. 시각화에 주로 사용.
- Linear Discriminant Analysis(LDA): 선형 분류 알고리즘으로 클래스 사이를 가장 잘 구분하는 축(이 측은 데이터가 투영되는 초평면을 정의한다)을 학습. 다른 분류 알고리즘을 적용하기 전에 차원을 축소 시키는 데 용이.
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기