차원의 저주
특성이 너무 많으면 차원이 커지고, 훈련을 느리게 하며 좋은 솔루션을 찾기 어려워진다. 이를 차원의 저주라고 한다. 그리고 차원이 너무 많으면 시각화를 하기에도 부적적해진다. 따라서 우리는 차원을 줄여야 한다. (물론 데이터들이 충분히 가까운 거리에 있을 때까지 데이터의 숫자를 늘릴 수도 있으나 말도 안되게 많은 숫자의 데이터가 필요해진다.)
Projection
훈련 샘플들은 고차원 안의 저차원 부분공간 안에 놓여 있는 경우가 많다. 따라서 불필요한 차원을 줄이고, 저차원으로 투영(projection)하여 차원을 줄일 수 있다.
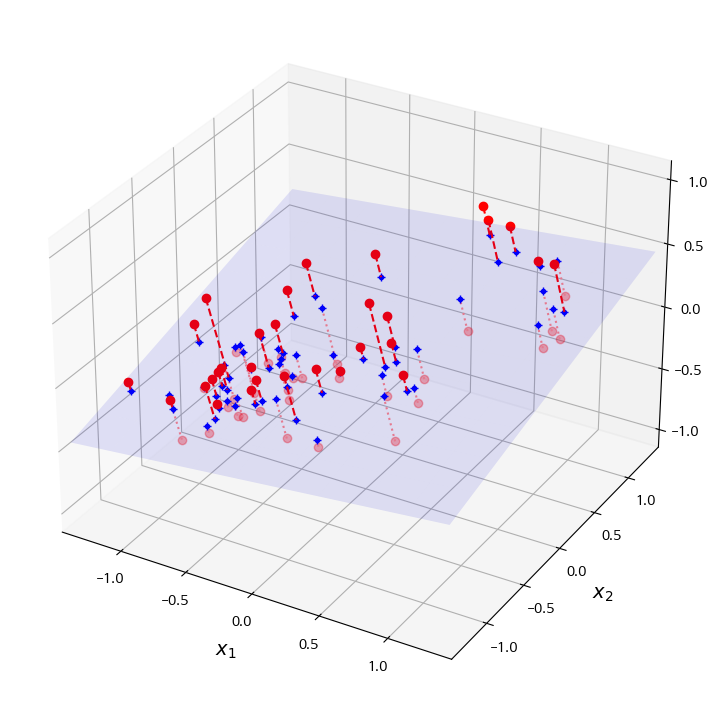
저차원으로 투영했을 때 데이터의 분포가 항상 유지되면 좋겠지만, 그렇지 않은 경우도 존재한다. 아래와 같은 스위스롤이 대표적인 예시이다.
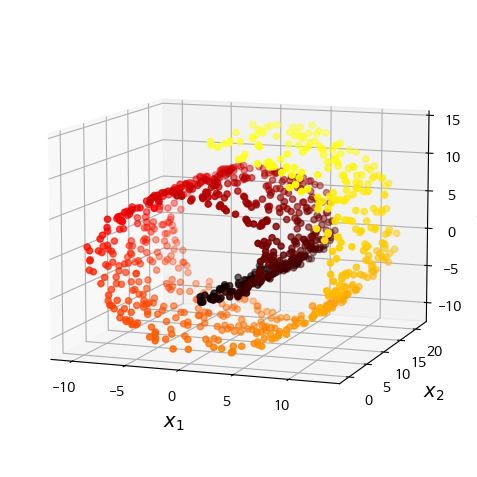
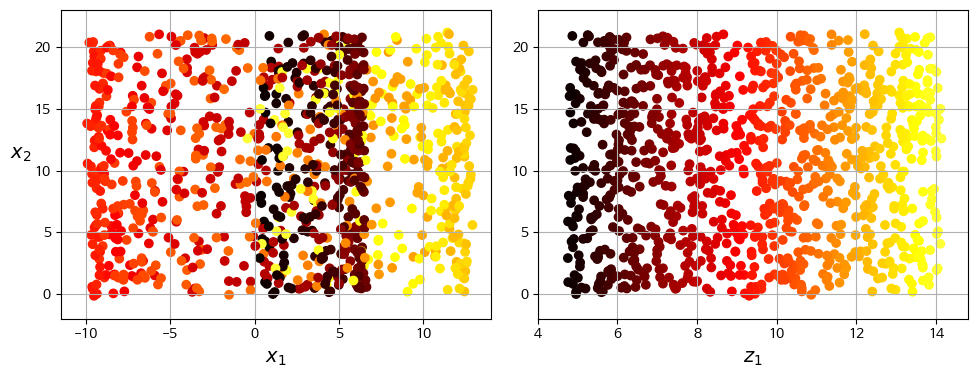
Manifold는 고차원 공간에서 휘거나 뒤틀린 저차원 공간의 모양이다. 더 일반적으로는, d차원 manifold는 국부적으로 d차원 초평면으로 보일 수 있는 n차원 공간의 일부이다(d $<$ n). 스위스롤은 2D manifold의 한 예시로. 국부적으로 2차원으로 보이는 3차원 공간의 일부이다.
많은 차원 축소 알고리즘은 훈련 샘플이 놓여있는 manifold를 모델링하는 방식으로 작동한다(manifold 학습). 이는 대부분 실제 고차원 dataset이 저차원 manifold에 가깝게 놓여있다는 manifold 가정(가설)에 근거를 두고 있다. 또한 이는 처리할 작업(분류나 회귀)이 저차원의 manifold 공간에 표현되면 더 간단해질 것이라는 가정과 동반된다. 하지만 이는 가정이므로 항상 유효한 것은 아니다.
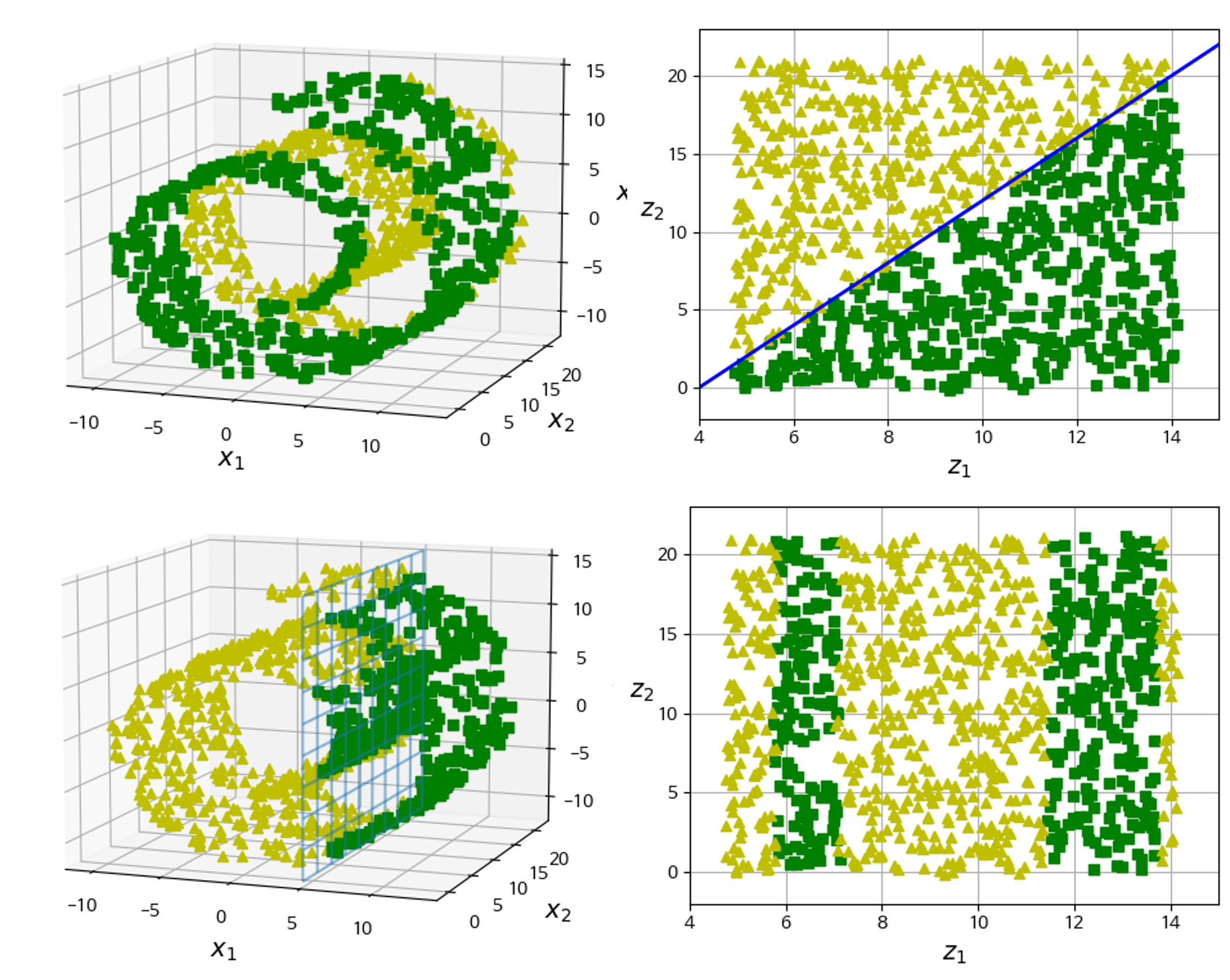
PCA
주성분 분석(Principal Component Analysis, PCA)는 가장 인기 있는 차원 축소 알고리즘이다. PCA를 위해서는 올바른 초평면을 선택하는 것이 중요한데, 분산을 최대한 보존하는 것이 중요하다.
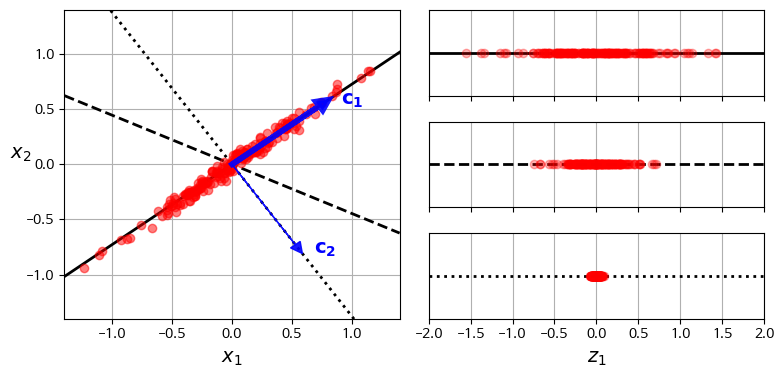
PCA는 다음과 같은 과정으로 진행된다.
- 분산을 최대로 보존하는 축을 찾는다.
- 1에서 찾은 축에 orthogonal이면서 남은 분산을 최대한 보존하는 두 번째 축을 찾는다.
- 2번 과정을 반복한다.
i번째 축은 i번째 주성분(PC)이 된다.
주성분은 Singular Value Decomposition(SVD)을 통해 찾을 수 있다. SVD는 train set 행렬 X를 다음과 같이 분해한다.
\[X = U \Sigma V^{T}\]우리가 찾는 주성분은 V에 column으로 들어가 있다. 코딩을 통해 구하는 과정은 다음과 같다.
X_centered = X - X.mean(axis=0) # PCA는 dataset의 평균이 0이라고 가정한다.
U, s, Vt = np.linalg.svd(X_centered)
c1 = Vt[0]
c2 = Vt[1]
d차원으로 투영하려면 X를 V의 처음 d개 column으로 이루어진 행렬과 곱해주면 된다.
\[X_{d_\proj} = X W_d\]코드로는 다음과 같다.
W2 = Vt[:2].T # 2차원으로 축소
X2D = X_centered.dot(W2)
사이킷런을 쓸 수도 있다. 사이킷런은 dataset의 평균을 자동으로 0으로 만들어준다. 따라서 별도의 전처리가 필요하지 않다.
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
X2D = pca.fit_transform(X)
pca.explained_variance_ratio_ # 분산 비율 출력 (어느 PC가 분산의 몇 %를 가지고 있는가)
적절한 차원의 수를 임의로 선택하기보다는 충분하 분산이 될 때까지 차원을 늘려가는 것이 좋다. 다음 코드는 분산의 95%를 보존하기 위한 코드이다.
from sklearn.datasets import fetch_openml
mnist = fetch_openml('mnist_784', as_frame=False)
X_train, y_train = mnist.data[:60_000], mnist.target[:60_000]
X_test, y_test = mnist.data[60_000:], mnist.target[60_000:]
pca = PCA()
pca.fit(X_train)
cumsum = np.cumsum(pca.explained_variance_ratio_) # cumsum: 입력 배열의 원소를 차례로 누적합 한 배열 반환
d = np.argmax(cumsum >= 0.95) + 1
pca = PCA(n_components=0.95) # 분산의 비율 지정
X_reduced = pca.fit_transform(X_train)
하이퍼파라미터 튜닝을 하듯이 차원 수를 튜닝할 수도 있다. 자세한 것은 코드를 참고하자.
압축된 데이터를 다시 원래 차원으로 복구할 수도 있다. 물론 이미 정보가 유실된 후이기 때문에 완벽한 원본 데이터셋을 얻을 수는 없으나, 결과는 꽤 괜찮다.
X_recovered = pca.inverse_transform(X_reduced)
근삿값을 빠르게 찾고 싶다면 Randomized PCA를 사용할 수도 있다. 처음 d개 주성분에 대한 근삿값을 빠르게 찾아준다.
rnd_pca = PCA(n_components=154, svd_solver="randomized", random_state=42)
X_reduced = rnd_pca.fit_transform(X_train)
cf.
svd_solver의 기본 값은 ‘auto’이다. max(m, n) $>$ 500 이고, n_components가 min(m, n)의 80%보다 작다면 자동으로 Randomized PCA를 수행한다. 따라서 자동으로 Randomized PCA가 되는 것을 막으려면 ‘full’로 설정해주어야 한다.
Incremental PCA(IPCA)는 점진적인 PCA 방식으로, 모든 데이터를 메모리에 올려 SVD를 수행해야 하는 기존 방식의 문제점을 보완한 것이다. Train set을 mini-batch로 나눈 뒤 ICPA 알고리즘에 하나씩 주입해 PCA를 진행한다.
from sklearn.decomposition import IncrementalPCA
n_batches = 100
inc_pca = IncrementalPCA(n_components=154)
for X_batch in np.array_split(X_train, n_batches):
inc_pca.partial_fit(X_batch)
X_reduced = inc_pca.transform(X_train)
Numpy의 mummap 클래스를 사용하여 디스크의 이진 파일에 저장된 train set을 마치 메모리에 있는 것처럼 조작할 수도 있다. 자세한 과정은 코드를 참고하자.
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기