결정 트리
결정 트리(Decision Tree)는 분류, 회귀 다중 출력 작업 모두에 사용할 수 있다. 또한 매우 복잡한 데이터셋도 학습할 수 있다.
결정 트리는 말 그대로 (뒤집힌) 나무의 모양을 하고 있다. 아래 그림은 결정 트리 분류로부터 나온다.
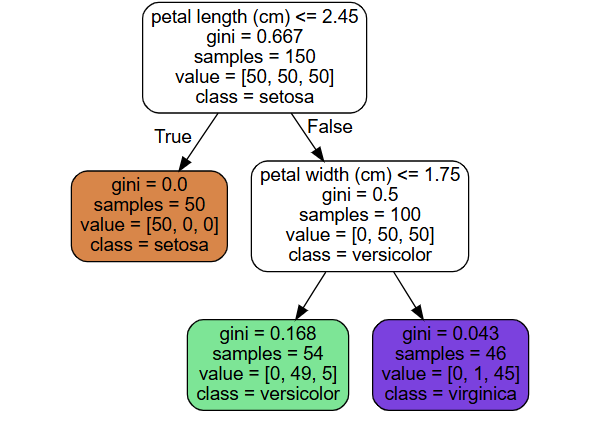
- 루트 노드: 가장 위 노드.
- 리프 노드: 더 이상 자식 노드를 가지지 않는 노드.
- 분할 노드: 자식을 가지는 노드.
각 노드에는 분류 기준과 함께 지니 불순도, 샘플 수, 클래스 등이 표기되어 있다.
결정 트리로 분류, 회귀 예측을 하는 방법은 매우 간단하다. 어떤 샘플에 대해 루트 노드부터 기준에 따라 트리 아래로 내려오면 된다.
결정 트리 예측은 $O(\log_2(m))$ 개의 노드를 거쳐야 한다. 예측에 필요한 전체 복잡도가 특성 수와 무관한 것이다. 따라서 큰 train set에서도 빠르게 예측할 수 있다. 한편, 훈련의 복잡도는 $O(n \times m \log_2(m))$이다.
cf. 결정 트리 알고리즘은 데이터 전처리(스케일링)가 거의 필요하지 않다. 다만, 아래에서 살펴볼 데이터의 축과 관련된 문제에서는 전처리를 해주는 것이 좋다.
결정 트리 분류
결정 트리 분류를 진행하는 코드는 다음과 같다.
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
iris = load_iris(as_frame=True)
X_iris = iris.data[['petal length (cm)', 'petal width (cm)']].values
y_iris = iris.target
tree_clf = DecisionTreeClassifier(max_depth=2, random_state=42)
tree_clf.fit(X_iris, y_iris)
앞서 살펴본 그림과 같이 결정 트리를 시각화하려면 다음 코드를 사용한다.
# 결정 트리 시각화
from sklearn.tree import export_graphviz
export_graphviz(
tree_clf,
out_file='iris_tree.dot', # 파일명
feature_names=['petal length (cm)', 'petal width (cm)'],
class_names=iris.target_names, # 클래스 이름 (회귀 때는 사용 X)
rounded=True,
filled=True
)
from graphviz import Source
Source.from_file('iris_tree.dot')
각 클래스에 속할 확률도 계산할 수 있다.
tree_clf.predict_proba([[5, 1.5]]).round(3)
지니 불순도와 엔트로피 불순도
지니 불순도는 이름에서 알 수 있듯이 한 노드의 훈련 샘플이 얼마나 순도가 높은지를 계산한다. 즉, 한 노드에 대해, 모든 샘플이 같은 클래스라면 순수(gini=0) 노드이고, 지니 불순도는 0이다. 공식은 다음과 같다.
\[G_i = 1 - \displaystyle \sum_{k=1}^{n}^2}\]- $G_i$ 는 i번째 노드의 지니 불순도이다.
- ${p_{i, k}}^2$ 는 i번째 노드에 속한 훈련 샘플 중 클래스 k에 속한 샘플의 비율이다.
기본적으로 지니 불순도를 사용하지만, 엔트로피 불순도를 쓸 수도 있다.
\[H_i = - \displaystyle \underset{p_{i, k} \neq 0} {\sum_{k=1}^{n}}{p_{i, k} \log_2{p_{i, k}}}\]그럼 무엇을 써야 할까? 지니 불순도의 계산이 더 빠르기 때문에, 기본적으로는 지니 불순도를 사용한다. 하지만 균형잡힌 트리를 만들고 싶다면 엔트로피 불순도를 사용한다.
CART 훈련 알고리즘
앞서 결정 트리를 통해 예측을 어떻게 하는지는 알아보았다. 그럼 결정 트리 자체를 훈련시키려면 어떻게 할까? CART(Classification And Regression Tree) 알고리즘을 사용한다.
-
train set를 하나의 특성 k의 임곗값 $t_k$ 를 사용해 두 개의 subset으로 나눔 (e.g. 꽃잎의 길이 $\leq$ 2.45cm).
이때, k와 $t_k$ 는 다음 비용 함수를 최소화하는 값으로 고른다. 아래 비용 함수를 최소화하는 것은 곧 크기에 따른 가중치가 적용된 가장 순수한 subset을 찾는 것이다.
\[J(k, t_k) = \frac{m_{left}}{m}G_{left} + \frac{m_{right}}{m}G_{right}\] - 같은 방식으로 subset을 계속해서 나누어감.
- 더 이상 subset을 나눌 수 없거나 중지 조건에 도달하면 멈춤.
위 방법에서 볼 수 있듯이, CART 알고리즘은 탐욕 알고리즘이다. 또한, CART 알고리즘은 기본적으로 이진 트리를 만든다.
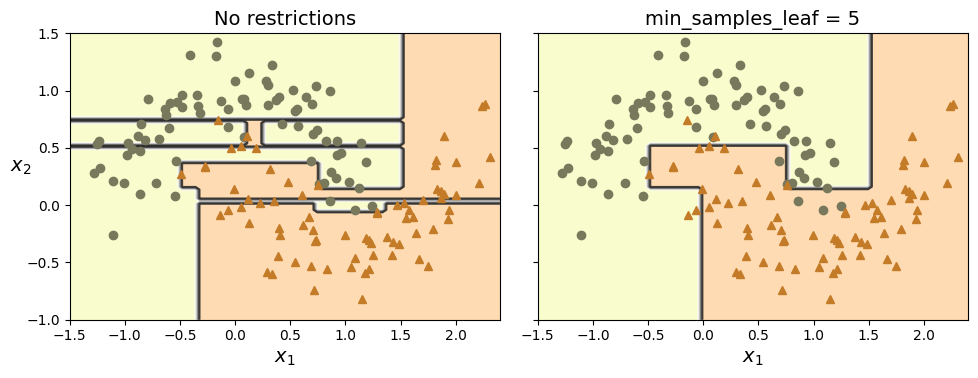
규제 파라미터
결정 트리는 비파라미터 모델(nonparametric model)이다. 훈련 되기 전에 파라미터 수가 결정되지 않는다는 뜻이다. 따라서 모델 구조가 데이터에 맞춰져서 고정되지 않고 자유롭다(과대적합될 위험이 커진다).
결정 트리에서는 다양한 하이퍼파라미터를 이용해서 과대적합을 방지할 수 있다.
| 하이퍼파라미터 | 의미 |
|---|---|
max_depth |
결정 트리의 최대 깊이 |
max_features |
각 노드에서 분할에 사용할 특성의 최대 수 |
max_leaf_nodes |
리프 노드의 최대 수 |
min_samples_split |
분할되기 위해 노드가 가져야 하는 최소 샘플 수 |
min_samples_leaf |
리프 노드가 생성되기 위해 가져야 하는 최소 샘플 수 |
min_weight_fraction_leaf |
min_samples_leaf와 같지만 가중치가 부여된 전체 샘플 수에서의 비율 |
min으로 시작하는 매개 변수를 늘리거나 max로 시작하는 매개변수를 줄이면 규제가 커지고, 과대적합을 방지할 수 있다.
결정 트리 회귀
import numpy as np
from sklearn.tree import DecisionTreeRegressor
np.random.seed(42)
X_quad = np.random.rand(200, 1)
y_quad = X_quad ** 2 + 0.025 * np.random.randn(200, 1)
tree_reg = DecisionTreeRegressor(max_depth=2, random_state=42)
tree_reg.fit(X_quad, y_quad)

결정 트리 회귀에서 분류와의 차이는 각 노드에서 클래스 대신 값을 예측한다는 것이다. 리프 노드의 평균 타깃값이 예측 값이 된다.
회귀에서는 불순도 대신 MSE를 최소화하는 방향으로 CART 알고리즘의 훈련이 진행된다.
\[J(k, t_k) = \frac{m_{left}}{m}MSE_{left} + \frac{m_{right}}{m}MSE_{right}\]축 방향에 대한 민감성
결정 트리는 축의 방향(데이터의 방향)에 민감하다. 다음 두 예시를 비교해보자.
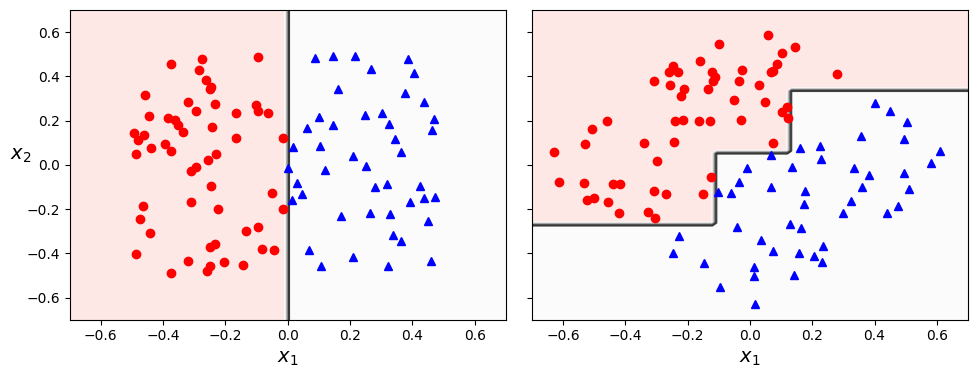
이를 해결하는 방법은 데이터의 스케일을 조정하고 PCA를 사용하는 것이다.
from sklearn.decomposition import PCA
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
pca_pipeline = make_pipeline(StandardScaler(), PCA())
X_iris_rotated = pca_pipeline.fit_transform(X_iris)
tree_clf = DecisionTreeClassifier(max_depth=2, random_state=42)
tree_clf.fit(X_iris_rotated, y_iris)
결정 트리의 분산 문제
결정 트리는 분산이 상당히 크다. 하이퍼파라미터나 데이터를 조금만 변경해도 완전히 다른 모델이 생성될 수 있다. 또한 사이킷런의 훈련 알고리즘은 확률적이므로(각 노드에서 평가할 특성 집합을 랜덤하게 선택), 같은 데이터로 재훈련하더라도 완전히 다른 모델이 만들어진다.
이를 해결하기 위해서는 결정 트리의 예측을 평균(앙상블)하면 된다. 이를 랜덤 포레스트라고 한다.
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기