SVM 이론
선형 SVM 분류기 모델은 단순히 결정 함수 $\mathbf{\theta^Tx} = \theta_0 x_0 + … + \theta_n x_n$ 을 계산해서 새로운 샘플 $\mathbf{x}$ 의 클래스를 예측한다. 결과에 따른 클래스는 다음과 같다.
- 결과가 0보다 큰 경우: $\hat{y}$ 는 양성 클래스(1)
- 결과가 0보다 작은 경우: $\hat{y}$ 는 음성 클래스(0)
우리의 목표를 다시 생각해보자. 마진을 넓히면서(도로 너비를 늘리면서), 동시에 마진 오류를 피하고 싶었다. 마진은 가중치 벡터 $\mathbf{w}$ 에 의해 결정된다. $\mathbf{w}$ 가 작을수록 마진이 커진다.
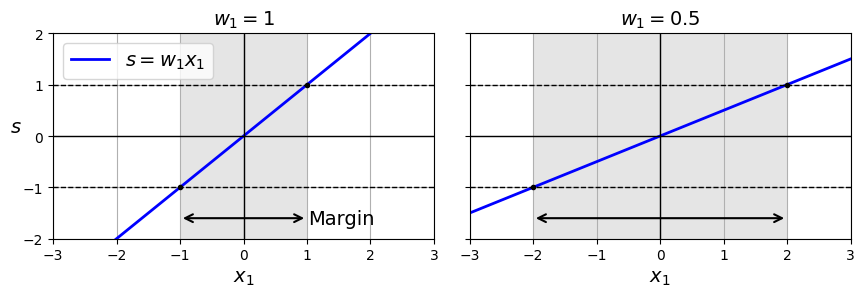
마진 오류를 줄이려면 결정 함수의 결과가 다음과 같아야 한다.
- 모든 양성 훈련 샘플: $ > 1 \quad \rightarrow \quad t^{(i)} = 1$
- 모든 음성 훈련 샘플: $ < -1 \quad \rightarrow \quad t^{(i)} = -1$
각 경우에 대해 t를 오른쪽과 같이 정의할 수 있다. 그럼 마진의 크기와 마진 오류를 합쳐서 다음과 같이 표현할 수 있다.
\[t^{(i)}(\mathbf{w^Tx^{(i)}} + b) \geq 1\]그럼 하드 마진 선형 SVM 분류기의 목적함수를 다음과 같은 최적화 문제로 표현할 수 있다.
\[\underset{w, b}{minimize} \; \frac{1}{2} \mathbf{w^T w}\]조건: $i=1, 2, …, m$ 일 때, $t^{(i)}(\mathbf{w^Tx^{(i)}} + b) \geq 1$
하지만 우리가 풀 문제는 하드 마진 분류가 아니고 소프르 마진 분류이다. 여기에는 슬랙 변수 $\zeta^{(i)} \geq 0$ 를 도입하는데, 이는 i번째 샘플이 얼마나 마진을 위반할지를 결정한다. 아래 소프트 마진 분류의 목적 함수는 두 가지 상충되는 목표를 가지고 있다.
- 마진 오류 최소화: $\zeta$ 를 가능한 작게
- 마진 최대화: $\frac{1}{2} \mathbf{w^T w}$ 를 가능한 작게
조건: $i=1, 2, …, m$ 일 때, $t^{(i)}(\mathbf{w^Tx^{(i)}} + b) \geq 1 - \zeta^{(i)}$ 이고, $\zeta^{(i)} \geq 0$
위와 같이 선형적인 제약조건이 있는 볼록 함수의 이차 최적화 문제를 콰드라틱 프로그래밍(QP)이라고 한다.
훈련 방법에는 두 가지가 있다.
- QP solver
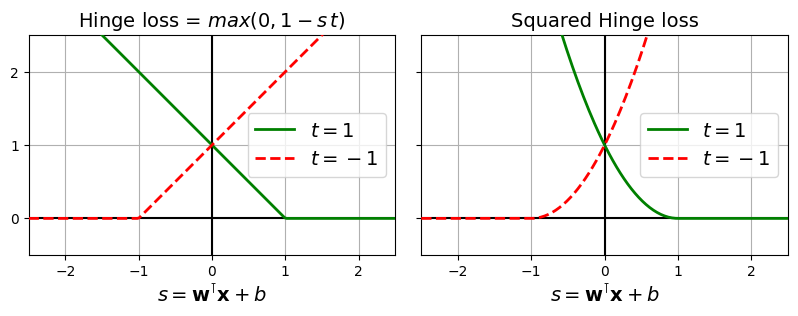
- 경사하강법: 힌지 손실이나 제곱 힌지 손실을 최소화.
제곱 힌지 손실은 이상치에 더 민감하지만, 이상치가 없다면 더 빠르게 수렴한다. LinearSVC는 제곱 힌지 손실, SGDClassifier는 힌지 손실을 사용한다 그래서 . 물론 LinearSVC가 더 빠른거구나loss 하이퍼파라미커를 hinge 또는 squared_hinge로 설정해줄 수도 있다.
쌍대 문제
원 문제(primal proble)를 쌍대 문제(dual problem)으로 바꾸어서 해결할 수 있다. SVM 문제는 운 좋게도 바꾸어 풀어서 나온 해가 원 문제와 동일한 해인 경우이다(대부분은 하한 값만 제공한다). 선형 SVM 목적 함수의 쌍대 형식은 다음과 같다.
\[\underset{\alpha}{minimize} \; \frac{1}{2} \displaystyle \sum_{i=1}^{m} \sum_{j=1}^{m} {\alpha^{(i)} \alpha^{(j)} t^{(i)} t^{(j)} \mathbf{x^{(i)^T}}x^{(j)}} - \sum_{i=1}^{m}{\alpha^{(i)}}\]QP 솔버를 이용해서 위 식을 최소화하는 vector $\mathbf{\hat{\alpha}}$ 를 찾았다면 다음과 같이 $\mathbf{\hat{w}}$, $\mathbf{\hat{b}}$ 를 구할 수 있다 ($n_s$ 는 서포트 vector의 개수).
$\mathbf{\hat{w}} = \displaystyle \sum_{i=1}^{m}{\hat{\alpha}^{(i)}} t^{(i)} \mathbf{x^{(i)}}$
$\mathbf{\hat{b}} = \frac{1}{n_s} \displaystyle \underset{\hat{\alpha}^{(i)} > 0} {\sum_{i=1}^{m}}{t^{(i)} - \mathbf{\hat{w}^Tx^{(i)}}}$
커널 트릭
이전 문단의 내용을 바탕으로 커널 트릭이 어떤 원리에서 가능한 것인지 알아보자.
다음은 우리가 적용하고자 하는 2차 다항식 매핑 함수 $\phi$ 이다.
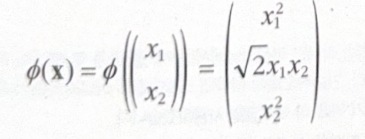
두 개의 vector에 대해 점곱을 하면 어떻게 되는지 보자.
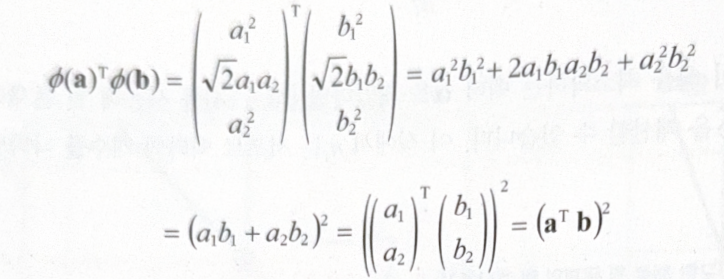
변환된 vector의 점곱이 원래 vector의 점곱의 제곱과 같다.
\[\phi{(\mathbf{a})}^T \phi{(\mathbf{b})} = (\mathbf{a^T b})^2\]모든 훈련 샘플에 변환 $\phi$ 를 적용하면 앞서 살펴본 쌍대 문제의 식에도 점곱 $\phi{(\mathbf{x^{(i)}})}^T \phi{(\mathbf{x^{(j)}})}$ 가 포함될 것이다. 하지만 이는 간단하게 $(\mathbf{x^{(i)^T x^{(j)}}})^2$ 로 바꿀 수 있다. 이와 같은 과정을 통해 실제로 훈련 샘플을 변환하지 않고 특성을 추가할 수 있는 것이다.
여기서 살펴본 다항식 커널 외에도 선형 커널, 가우스 RBF 커널 등이 있다.
그러나 아직 해결하지 못한 부분이 있다. 바로 차원에 관한 문제이다. $\phi{(\mathbf{x^{(i)}})}$ 의 차원은 매우 크거나 무한한데, 이를 $\hat{\mathbf{w}}$ 와 matirx 곱을 해야 하기 때문이다. 다행히도 $\hat{\mathbf{w}}$ 없이 입력 vector 의 점곱만으로도 해결이 가능하다.
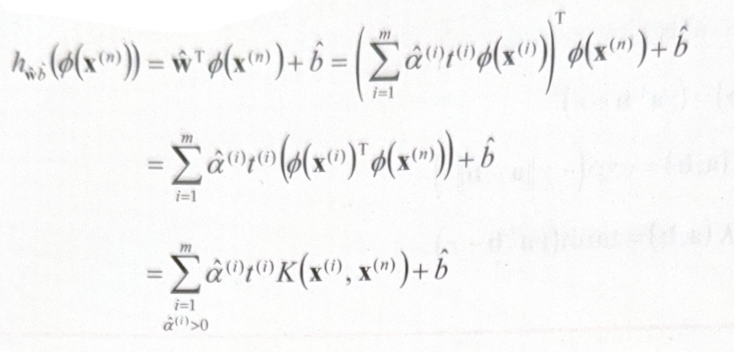
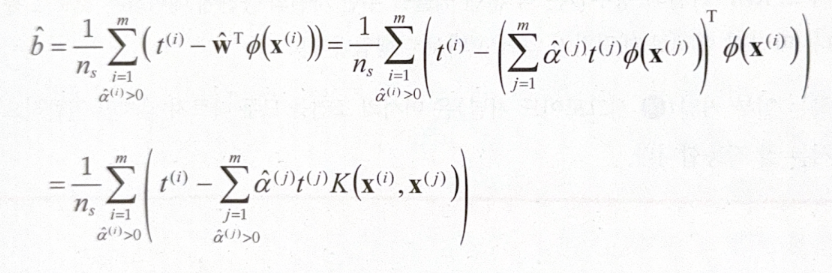
복잡한 수식이 너무 많아서 어지럽지만, 책에 따르면 이 또한 커널 트릭의 부수적 효과라고 한다.
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기