학습 곡선
학습 곡선은 training set의 크기에 대한 오차(RMSE)를 그래프로 나타낸 것이다. 이를 활용하면 모델이 과대적합인지 과소적합인지를 판별할 수 있다.
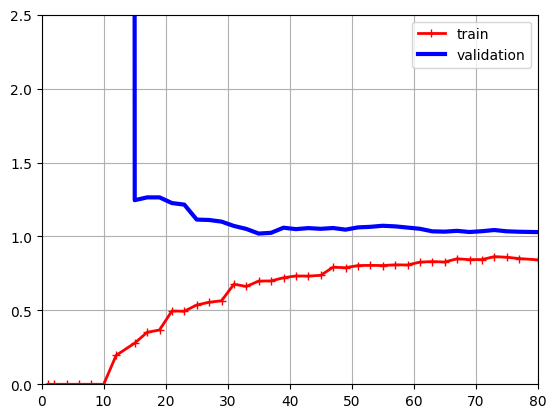
다음은 차례대로 선형 회귀, 10차 다항 회귀의 학습 곡선이다. (자세한 코드는 마지막에 있는 링크를 참고.)
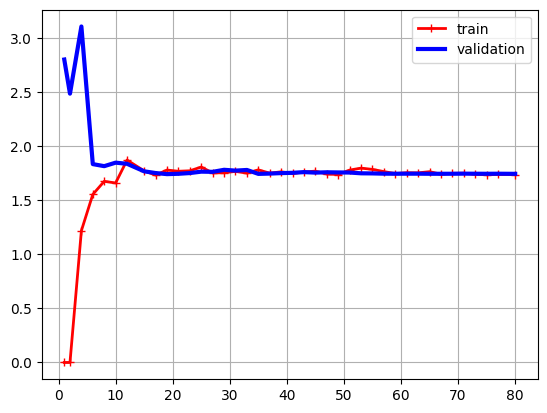
먼저 선형 회귀 그래프는 전형적인 과소적합이다. Training set과 dev set의 그래프가 매우 가까워지며, 그 오차 값이 꽤 크다. 이는 모델이 training set과 dev set 둘 다 일반화하지 못했다는 뜻이다.
반대로 다항 회귀 그래프는 과대적합이다. 선형 회귀와 비슷해 보이지만 두 가지 큰 차이점이 있다.
- 오차가 낮다.
- 두 곡선이 가까워지기는 하지만 사이에 공간이 있다. 특히 두 곡선 사이에 공간이 있다는 말은 training set에서의 성능이 더 좋다는 의미로, 과대적합을 의미한다.
편향(bias, 높으면 과소적합)과 분산(variance, 높으면 과대적합) 사이에는 trade-off가 존재한다. 둘 다 동시에 줄일 수는 없다는 뜻이다.
규제가 있는 선형 모델
다항 모델의 과대적합을 해결하는 방법은 차수를 줄이는 것이다. 선형 모델에서는 모델의 가중치를 제한함으로써 규제를 가한다. 다양한 방법들을 살펴보자.
규제 1 - Ridge Regression
Ridge Regreession은 다음과 같은 비용 함수를 사용한다.
\[J(\theta) = MSE(\theta) + \frac{\alpha}{m} \sum_{i=1}^{n}{\theta_i^{2}}\]위 비용 함수는 훈련하는 동안에만 사용하며, 훈련이 끝나면 규제를 없앤다. 편향에는 규제를 추가하지 않는다. 규제를 사용하기 전에 반드시 StandardScaler로 스케일을 맞추어 주어야 한다.
$\alpha$ 는 하이퍼파라미터로, 모델을 얼마나 많이 규제할지 조절한다. 클수록 규제가 강해진다. $\mathbf{w}$ 를 특성 가중치 vector라고 정의하면 규제 항은 $\alpha \frac{(\Vert x \Vert_2)^2}{m}$ 가 된다. Batch gradient descent에 적용하려면 $\frac{2 \alpha \mathbf{w}}{m}$ 를 더한다.
정규방정식 버전은 다음과 같다.
\[\hat{\theta} = (X^{T}X + \alpha A)^{-1}X^{T} \mathbf{y}\]구현은 이렇게 한다.
# 정규방정식 사용
from sklearn.linear_model import Ridge
ridge_reg = Ridge(alpha=0.1, solver='cholesky')
ridge_reg.fit(X, y)
ridge_reg.predict([[1.5]])
# SGD에서의 사용
sgd_reg = SGDRegressor(penalty='l2', alpha=0.1 / m, tol=None, max_iter=1000, eta0=0.01, random_state=42)
sgd_reg.fit(X, y.ravel())
sgd_reg.predict([[1.5]])
penalty='l2'로 지정하여 $l_2$ norm을 사용한다. m으로 나누지 않는 것을 사용하면 ridge regression과 같기에, alpha=0.1 / m를 통해 완벽한 ridge regression을 구현하였다.
규제 2 - Lasso Regression
Lasso(Least Absolute Shrinkage and Selection Operator) Regression은 ridge의 $l_2$ norm 대신 $l_1$ norm을 더한다.
\[J(\theta) = MSE(\theta) + 2 \alpha \sum_{i=1}^{n}{\vert \theta_i \vert}\]Lasso의 가장 중요한 특징은 덜 중요한 특성의 가중치를 0으로 만든다(제거)는 것이다. 자동으로 특성 선택을 하는 셈이다.
Lasso의 비용 함수는 0에서 미분 가능하지 않다. 이게 걸린다면 Subgradiet vector g를 사용하면 된다.
Lasso의 구현은 다음과 같다.
from sklearn.linear_model import Lasso
lasso_reg = Lasso(alpha=0.1)
lasso_reg.fit(X, y)
lasso_reg.predict([[1.5]])
규제 3 - Elastic Net
Ridge와 Lasso 중 하나를 선택하기 어렵다면 결정 장애 이를 절충한 elastic net을 사용하면 된다. 두 규제의 항을 단순히 더한 뒤 혼합 비율 r을 둔 것이다.
from sklearn.linear_model import ElasticNet
elastic_net = ElasticNet(alpha=0.1, l1_ratio=0.5)
elastic_net.fit(X, y)
elastic_net.predict([[1.5]])
Early Stopping
조기 종료(Early stopping)는 검증 오차가 최솟값에 도달하면 바로 훈련을 종료시키는 것이다.
from copy import deepcopy
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import StandardScaler
# 데이터셋 생성은 생략
preprocessing = make_pipeline(PolynomialFeatures(degree=90, include_bias=False),
StandardScaler())
X_train_prep = preprocessing.fit_transform(X_train)
X_valid_prep = preprocessing.transform(X_valid)
sgd_reg = SGDRegressor(penalty=None, eta0=0.002, random_state=42)
n_epochs = 500
best_valid_rmse = float('inf') # 최고 rmse를 양의 무한대로 지정
for epoch in range(n_epochs):
sgd_reg.partial_fit(X_train_prep, y_train)
y_valid_predict = sgd_reg.predict(X_valid_prep)
val_error = mean_squared_error(y_valid, y_valid_predict, squared=False)
if val_error < best_valid_rmse: # 오차 대소 판단
best_valid_rmse = val_error
best_model = deepcopy(sgd_reg)
코드의 핵심만 살펴보면, 일단 최고 검증 오차(best_valid_rmse)를 무한대로 설정한다. 그리고 학습이 진행되면서 해당 epoch의 검증 오차가 지금까지 최고의 검증오차보다 작으면 (val_error < best_valid_rmse) 모델을 저장한다. 이는 실제로 학습을 종료하지는 않지만, 모델을 저장해서 불러올 수 있다는 효과가 있다.
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기