이번 chapter에서는 손글씨 dataset인 MNIST를 이용해서 분류에 대해 학습한다.
이항 분류기 훈련
복잡한 분류를 하기 전에 손글씨가 5인지 아닌지만을 판단하는 이항 분류기를 훈련해본다.
y_train_5 = (y_train == '5')
y_test_5 = (y_test == '5')
# 확률적 경사 하강법 사용
from sklearn.linear_model import SGDClassifier
sgd_clf = SGDClassifier(random_state=42)
sgd_clf.fit(X_train, y_train_5)
교차 검증을 통한 성능 측정
k-폴드 교차 검증을 통해 정확도(accuracy)를 측정하면 정확도가 매우 높게 나오는 것을 확인할 수 있다. 하지만 모든 데이터를 음성 클래스로 예측하더라도 정확도가 비슷하게 나오는 것을 확인할 수 있다. 이는 마치 비가 안 올 것이라고 1년 내내 일기예보를 하면서 정확도가 70%가 넘는다고 자랑하는 것과 동일하다. 즉, 불균형한 dataset을 다룰 때는 정확도를 성능 측정의 지표로 사용해서는 안된다.
오차 행렬
모든 A/B 쌍에 대해 클래스 A의 샘플이 클래스 B로 분류된 횟수를 세는 오차 행렬을 사용한다면 좀 더 효과적으로 성능을 측정할 수 있다.
>>> from sklearn.metrics import confusion_matrix
>>> cm = confusion_matrix(y_train_5, y_train_pred)
array([[53892, 687],
[ 1891, 3530]])
오차 행렬에서 행은 실제 클래스를, 열은 예측한 클래스를 나타낸다. 위 결과에서 첫 번째 행은 ‘5 아님’ 클래스(음성 클래스)이고, 두 번째 행은 ‘5임’ 클래스 (양성 클래스)이다. 오차 행렬을 해석하면
- 53892개의 이미지를 5아님으로 정확하게 분류했고(진짜 음성), 687개의 이미지를 5라고 잘못 분류하였다(거짓 양성).
- 3530개의 이미지를 5로 정확하게 분류하였고(진짜 양성), 1891개의 이미지를 5가 아니라고 잘못 분류하였다(거짓 음성).
정밀도와 재현율
정밀도(precision)는 양성 예측의 정확도로, 다음과 같이 계산한다.
\[Precision = \frac{TP}{TP + FP}\]재현율(recall)은 정확하게 감지한 양성 샘플의 비율로, 다음과 같이 계산한다.
\[Recall = \frac{TP}{TP + FN}\]쉽게 생각하면 다음과 같다.
- 정밀도: 분류기가 맞다고 분류한 것 중에 진짜 맞는 게 몇 개냐?
- 재현율: 분류기가 실제 타깃 중에 몇 개나 골라냈냐(얼마나 정답을 잘 재현해냈냐)?
코드는 다음과 같다.
from sklearn.metrics import precision_score, recall_score
precision_score(y_train_5, y_train_pred)
정밀도와 재현율을 합치면 $F_1$ 점수가 된다. 당연히 높을수록 좋다.
\[F_1 = \frac{2}{\frac{1}{precision} + \frac{1}{recall}} = \frac{TP}{TP + \frac{FN + FP}{2}}\]구현은 다음과 같다.
from sklearn.metrics import f1_score
f1_score(y_train_5, y_train_pred)
정밀도와 재현율을 모두 얻을 수는 없다. 이를 정밀도/재현율 트레이드오프라고 한다.
분류기는 결정함수를 사용해서 각 샘플의 점수를 계산하고, 미리 지정된 임곗값과 점수를 비교해 분류를 진행한다.
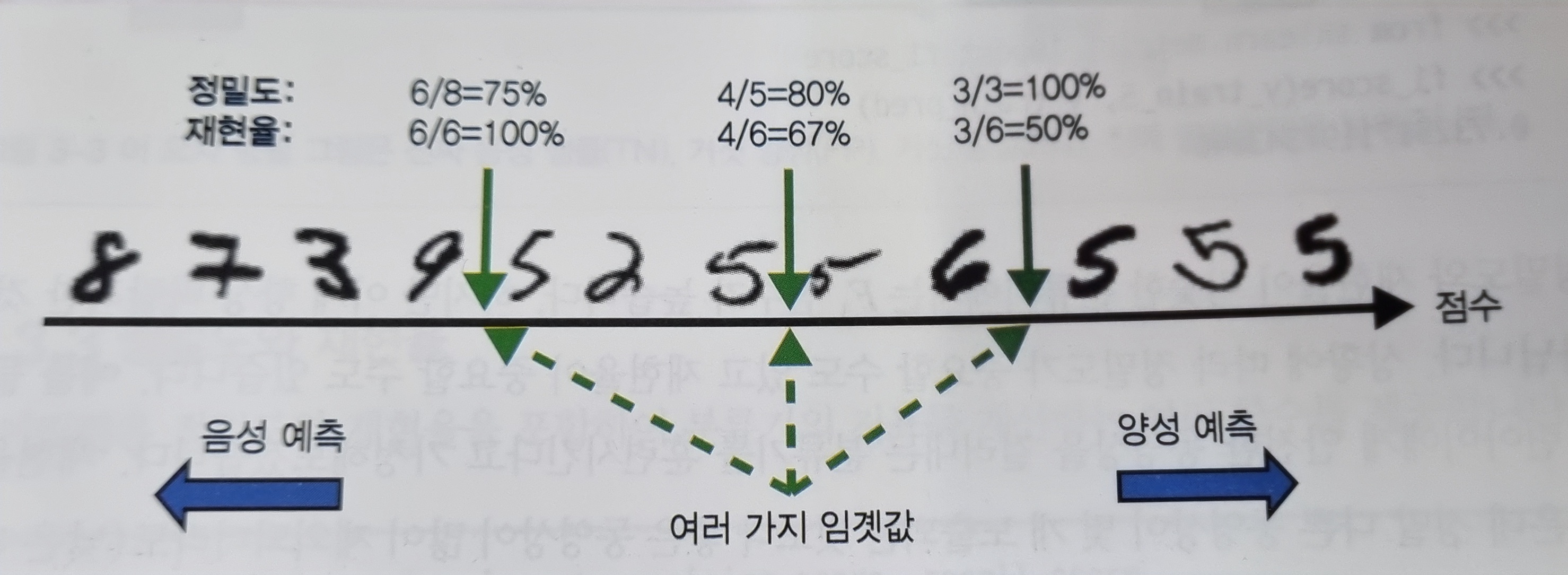
따라서 임곗값을 높이면 정밀도가 높아지는 대신 재현율이 줄어들고, 임곗값을 낮추면 재현율이 높아지는 대신 정밀도가 낮아지게 되는 것이다.
decision_function()을 사용하면 원하는 임곗값을 지정해서 예측을 만들 수 있다.
좋은 임곗값을 선택하려면 임곗값에 대한 정밀도와 재현율 그래프를 그리면 된다.
plt.plot(thresholds, precisions[:-1], 'b--', label='precision', linewidth=2)
plt.plot(thresholds, recalls[:-1], 'g-', label='recall', linewidth=2)
plt.vlines(threshold, 0, 1.0, 'k', 'dotted', label='threshold')
plt.show()
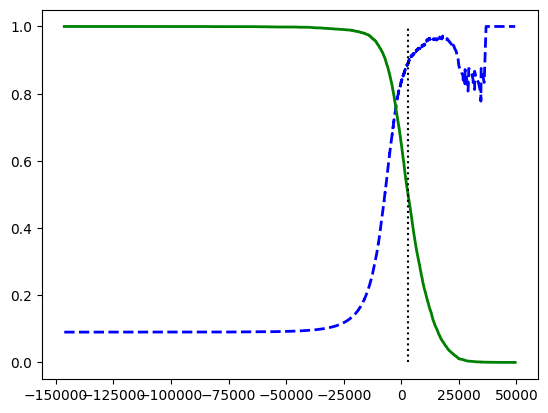
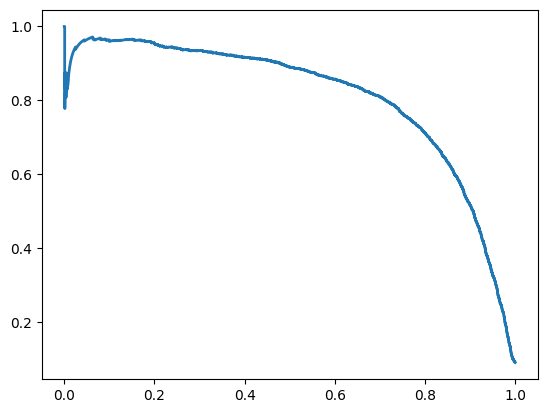
재현율에 대한 정밀도 그래프를 그리는 것도 도움이 된다.
plt.plot(recalls, precisions, linewidth=2, label='precision/recall curve')
plt.show()
ROC 곡선
수신기 조작 특성(Receiver Operating Characteristic, ROC) 곡선도 이항 분류에서 자주 사용된다. ROC 곡선은 거짓 양성 비율에 대한 진짜 양성 비율을 나타낸다. 거짓 양성 비율은 1에서 진짜 음성 비율을 뺀 값을 말한다.
그림으로 나타내는 코드는 다음과 같다.
from sklearn.metrics import roc_curve
fpr, tpr, thresholds = roc_curve(y_train_5, y_scores)
idx_for_threshold_at_90 = (thresholds <= threshold_for_90_precision).argmax()
tpr_90, fpr_90 = tpr[idx_for_threshold_at_90], fpr[idx_for_threshold_at_90]
plt.plot(fpr, tpr, linewidth=2, label='ROC curve')
plt.plot([0, 1], [0, 1], 'k--', label='ROC curve of random classifier') # 비교를 위한 랜덤 분류기 그래프
plt.plot([fpr_90], [tpr_90], 'ko', label='threshold for 90% precision')
plt.legend()
plt.show()
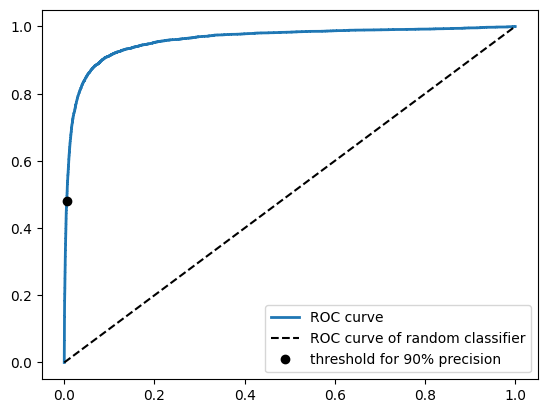
위 코드에는 비교를 위한 완전 랜덤 분류기 그래프가 있다. 해당 그래프에서 최대한 멀리(왼쪽 위로) 떨어져 있어야 좋은 분류기이다.
ROC 곡선에서는 곡선 아래의 면적(AUC)이 비교 척도가 된다. 적어도 랜덤 분류기의 넓이(0.5)보다는 넓어야 봐줄만한 분류기라고 할 수 있을 것이다.
from sklearn.metrics import roc_auc_score
roc_auc_score(y_train_5, y_scores)
추가로, 코드에는 랜덤 포레스트 분류기의 성능을 평가한 과정도 포함되어 있다.
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기