StyleGAN
StyleGAN uses style transfer technique at generator. The purpose is to make generated image have partial structures whice are similar to train images. Discriminator and loss function are preserved, and only generator was changed.
The structure of StyleGAN is as a following image.
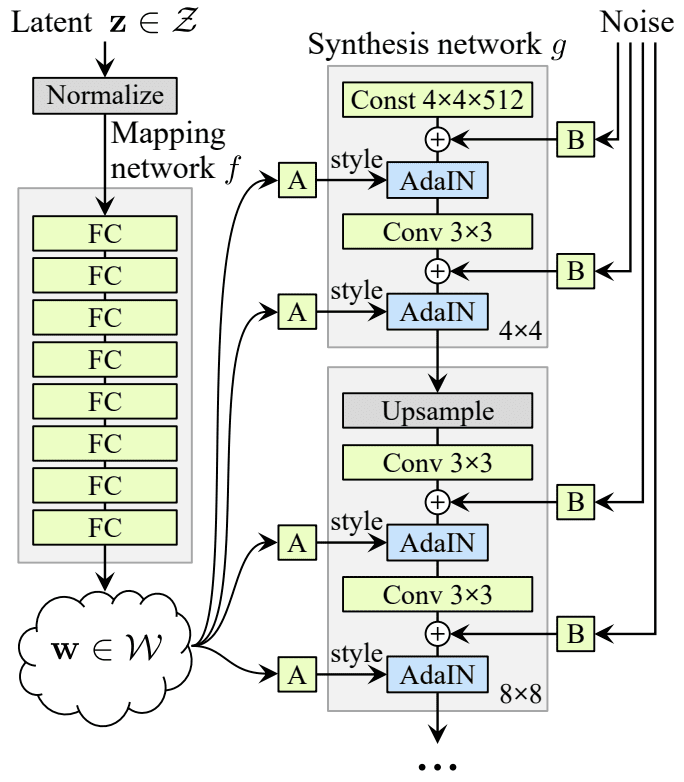
Two networks compose StyleGAN.
- Mapping Network: Eight MLP map latent representation z(coding) to vector w. The vector is delivered to affine transformation to generate multiple vectors, which controls from low-level characteristics to high-level characteristics. In other words, mapping network maps coding to multiple style vectors.
- Synthesis Network: Generate image. Image will go through multiple conv layers and upscaling layers. There are two key points. First, noise is added to input and all output of conv layers. Second, adaptive instance normalization(AdaIN) follows after adding noise. AdaIN is a process that normalizes each feature map independently and determines scale and offset of each feature map by using style vector.
Adding noise independently to coding is important. This can prevent the model to use its capacity to learn noise. On the other hand, if generator makes random noise by itself, it will look like artificial. By adding additional noise, the issues are solved.
At the last step, StyleGAN uses mixing regularization, which generates constant proportion of images with two different codings. To be specific, coding $\mathbf{c}_1$ and $\mathbf{c}_2$ passes mapping network and make two style vector $\mathbf{w}_1$, and $\mathbf{w}_2$. At the first phase of synthesis network, $\mathbf{w}_1$ is used. Then, at the rest phase, $\mathbf{w}_2$ is used. The turing point of style vector is randomly chosen. This process will prevent the network to assume that adjacent style have a correlation.
Diffusion Model
The idea of diffusion model is to reverse the diffusing process. If there is chocolate milk. our purpose is to separate milk and chocolate.
The most successful diffusion model is Denoising Diffusion Probabilistic Model(DDPM).
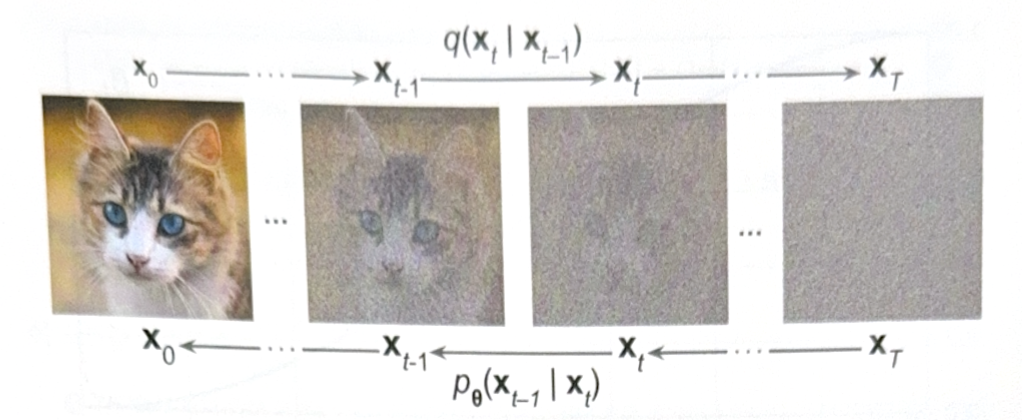
- Forward process
- Start at $\mathbf{x}_0$.
- For each time step, add gaussian noise(N(0, $\beta_t$)) to the image. The noise is independent to each pixel(it is called isotropic). Pixel value is also modified by a ratio $\sqrt{1-\beta_t}$.
- At final time step T, get an image without a cat.
The following is a formula of forward process.
\[q(\mathbf{x}_t | \mathbf{x}_{t-1}) = \mathcal{N}(\sqrt{1-\beta_t}\mathbf{x}_{t-1}, \beta_t \mathbf{I})\]However, there is a better way. Multiple sum of gaussian distribution is also gaussian, so the following formula is faster.
\[q(\mathbf{x}_t | \mathbf{x}_0) = \mathcal{N}(\sqrt{\bar{\alpha_t}}\mathbf{x}_0, (1 - \bar{\alpha_t}) \mathbf{I})\]Of course, our purpose is not making noise, is making a cat image!
- Reverse process
- Start at $\mathbf{x}_t$.
- Train model that can remove noise.
- Repeat until all noise disappear.
The following is an key implementation of DDPM. For full implementation, see ‘Go for Codes’.
# variance scheduling
def variance_schedule(T, s=0.008, max_beta=0.999):
t = np.arange(T + 1)
f = np.cos((t / T + s) / (1 + s) * np.pi / 2) ** 2
alpha = np.clip(f[1:] / f[:-1], 1 - max_beta, 1)
alpha = np.append(1, alpha).astype(np.float32)
beta = 1 - alpha
alpha_cumprod = np.cumprod(alpha)
return alpha, alpha_cumprod, beta
T = 4000
alpha, alpha_cumprod, beta = variance_schedule(T)
# make image with noise
def prepare_batch(X):
X = tf.cast(X[..., tf.newaxis], tf.float32) * 2 - 1
X_shape = tf.shape(X)
t = tf.random.uniform([X_shape[0]], minval=1, maxval=T + 1, dtype=tf.int32)
alpha_cm = tf.gather(alpha_cumprod, t)
alpha_cm = tf.reshape(alpha_cm, [X_shape[0]] + [1] * (len(X_shape) - 1))
noise = tf.random.normal(X_shape)
return {
"X_noisy": alpha_cm ** 0.5 * X + (1 - alpha_cm) ** 0.5 * noise,
"time": t,
}, noise
# reverse process
def generate(model, batch_size=32):
X = tf.random.normal([batch_size, 28, 28, 1])
for t in range(T - 1, 0, -1):
print(f"\rt = {t}", end=" ")
noise = (tf.random.normal if t > 1 else tf.zeros)(tf.shape(X))
X_noise = model({"X_noisy": X, "time": tf.constant([t] * batch_size)})
X = (
1 / alpha[t] ** 0.5
* (X - beta[t] / (1 - alpha_cumprod[t]) ** 0.5 * X_noise)
+ (1 - alpha[t]) ** 0.5 * noise
)
return X
tf.random.set_seed(42)
X_gen = generate(model)
The reverse process is an implementation of following formula.
\[\mathbf{x}_{t-1} = \frac{1}{\sqrt{\alpha_t}}(\mathbf{x}_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha_t}}}\mathbf{\epsilon_\theta}(\mathbf{x}_t, t)) + \sqrt{\beta_t}\mathbf{z}\]There are also more powerful model. Latent diffusion model performs the diffusion process in the latent space. Autoencoder will compress image to even smaller latent space, and then generate image by decompressing the representation.
All images, except those with separate source indications, are excerpted from lecture materials.

댓글남기기