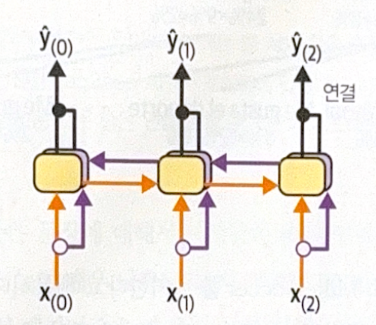
Bidirectional RNN
To distinguish homonyms according to the context, we should consider the next words, not only the previous ones. Therefore, two recurrent layers are needed, one for forward reading, and the other for backward reading. It is called bidirectional recurrent layer.
encoder = tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(256, return_state=True))
There is one problem. There will be 4 states, long-term and short-term for each layer. So, we will connect short-term and long-term state each.
class ConcatenateLayer(tf.keras.layers.Layer):
def call(self, inputs):
return tf.concat(inputs, axis=-1)
encoder_outputs, *encoder_state = encoder(encoder_embeddings)
encoder_state = [ConcatenateLayer()(encoder_state[::2]),
ConcatenateLayer()(encoder_state[1::2])]
Beam Search
The models we have learned until now could not modify wrong translations, if the word is determined once. Beam search is a method to solve the problem.
At beam search, top-k(beam width) possible senteneces are maintained in a list, and for each decoder step, possible k sentences are geneterated by using a word in the sentence.
The following is an example of beam width 3. Conditional probability will be used for the next step word.
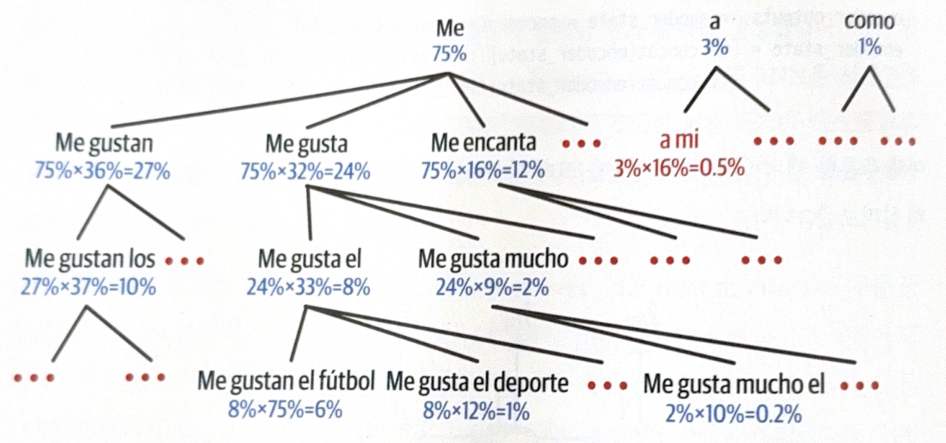
- Top-3 most highly likely words are selected.
- For the 3 words, all possbile sentences are generated.
- Conditinoal probability is calculated for each sentences.
- Among sentences in step 3, top-3 are selected.
- Repeat 3~5 until the sentence end.
- Pick a sentence with the highest probability.
Attention Mechanism
If a decoder can pay attention to the appropriate word for each time step, the route from input to translation will be shorten. This is called attention mechanism.
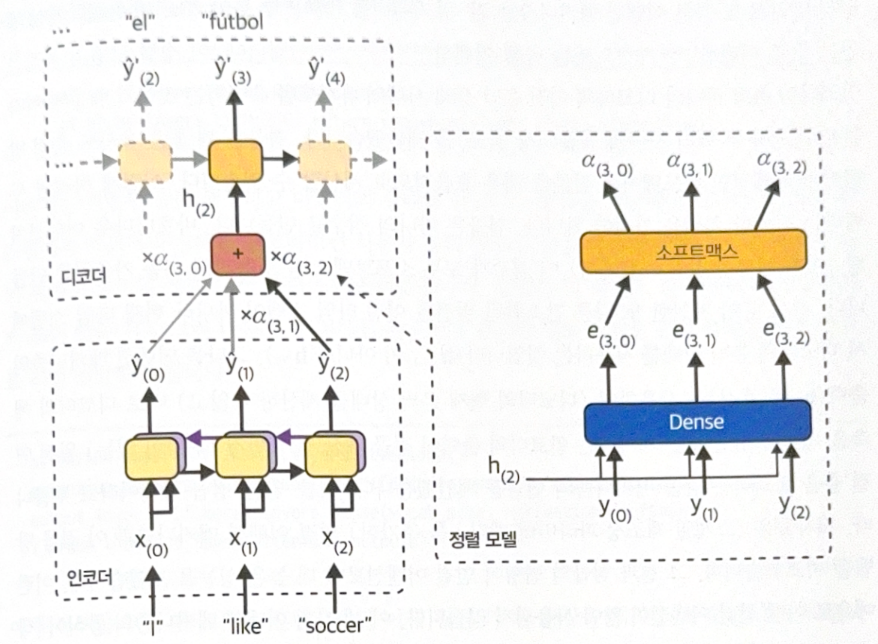
The left part of image is encoder-decoder. All output of encoder will be delivered to the decoder. As the decoder could not handle them at once, the weighted sum will be calculated. The word to pay attention is determined at the step. $\alpha_{(t, i)}$ is a weight of ith encoder output at time step t.
The right part of image is an alignment model, which generates weights, $\alpha_{(t, i)}$. The model is co-trained with the remaining part of encoder-decoder model. The following is a process of an alignment model.
- Dense layer with one neuron processes the ‘all outputs of encoder’ and ‘the prior hidden state of decoder(e.g. $h_{(2)}$)’.
- Return score(or energy) (e.g. $e_{(3, 0)}$) for each encoder input. The score means how each output fits well to the hidden state of decoder.
- Print the final weight for each input through softmax layer.
This kind of attention is called Bahdanau attention, or concatenative attention.
There is another well-known attention, called Luong attention(multiplicative attention). As the purpose of the alignment is to measure the similarity between the hidden state of decoder and the output of encoder, Luong attention uses dot product of two vectors.
There are some variations of Luong attention. Instead of the hidden state of previous step, the current hidden state of decoder could be used. Additionally, before calculating dot products, output of encoders pass through a fully connected layer. These variations work better than Bahdanau attention.
In keras, use tf.keras.layers.Attention for Luong, and use tf.keras.layers.AdditiveAttention for Bahdanau attention.
# Luong Attention
encoder = tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(256, return_sequences=True, return_state=True))
encoder_outputs, *encoder_state = encoder(encoder_embeddings)
encoder_state = [ConcatenateLayer()(encoder_state[::2]),
ConcatenateLayer()(encoder_state[1::2])]
decoder = tf.keras.layers.LSTM(512, return_sequences=True)
decoder_outputs = decoder(decoder_embeddings, initial_state=encoder_state)
decoder_outputs = tf.keras.layers.Lambda(lambda x: x)(decoder_outputs)
encoder_outputs = tf.keras.layers.Lambda(lambda x: x)(encoder_outputs)
attention_layer = tf.keras.layers.Attention()
attention_outputs = attention_layer([decoder_outputs, encoder_outputs])
output_layer = tf.keras.layers.Dense(vocab_size, activation='softmax')
Y_proba = output_layer(attention_outputs)
Set return_sequences=True in encoder to deliver all outputs to an attention layer. Instead of the hidden state of decoder, output of decoder also works fine.
Transformer
A transfomer structure only uses attention. It does not use RNN or CNN.
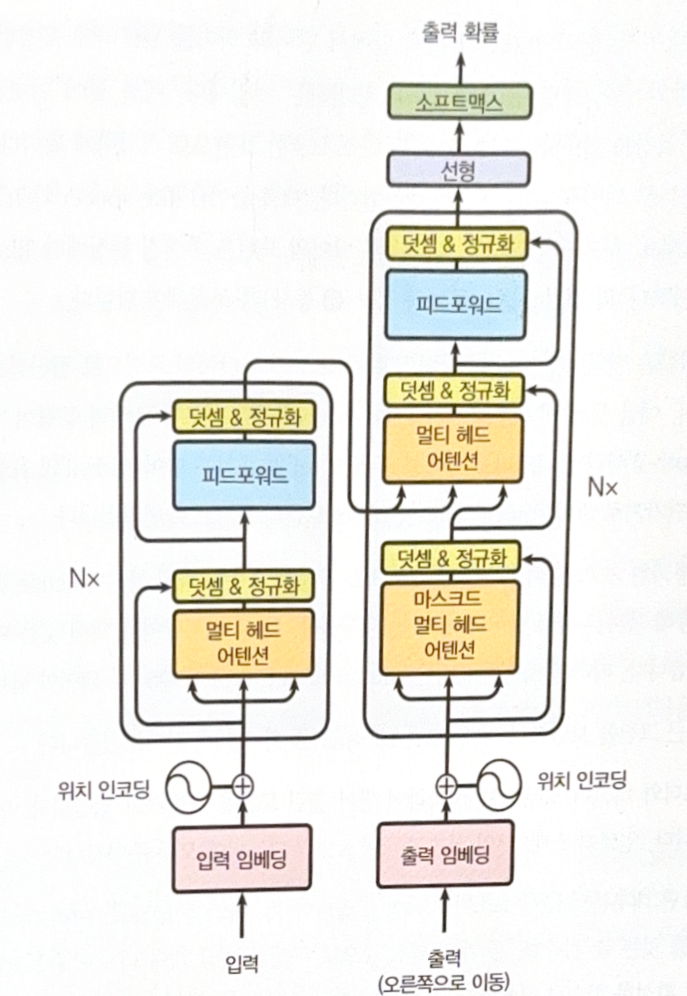
The left part of image is encoder, and the right part is decoder.
The role of encoder is to gradually transform the input until perfectly capturing the meaning of the word in the context.
The role of decoder is to gradually trasnform the translated expression into the next word of the sentence.
After passing the decoder, it passes the final dense layer. It expects the high probability for the correct word and the low probability for wrong words.
All layers are time-distributed(independnet) to time step. In other words, each word is processed independently to the other words. To enable this there are some special components.
- Multi-head attention of encoder: Update each word expression taking care of all other words in the sentence.
- Masked multi-head attention of decoder: Work similar to multi-head attention of encoder, but only cares about the previous words (causal).
- Multi-head attention of decoder: Take care of words in the original sentence (cross attention).
- Positional encoding: Represent the position of each word in the sentence. Without positional encoding, input sequence could be shuffled and the position info will disappear.
Positional Encoding
Positional encoding is a dense vector which encodes the positon of the words. ith positional encoding will be simply added to ith word embedding.
The simplest way to implement this is to encode all positions using Embedding layer, and add the output to the word embedding.
# positional encoding
max_length = 50
embed_size = 128
pos_embed_layer = tf.keras.layers.Embedding(max_length, embed_size)
batch_max_len_enc = tf.keras.layers.Lambda(lambda x: tf.shape(x)[1])(encoder_embeddings)
encoder_in = encoder_embeddings + pos_embed_layer(tf.keras.layers.Lambda(lambda x: tf.range(x))(batch_max_len_enc))
batch_max_len_dec = tf.keras.layers.Lambda(lambda x: tf.shape(x)[1])(decoder_embeddings)
decoder_in = decoder_embeddings + pos_embed_layer(tf.keras.layers.Lambda(lambda x: tf.range(x))(batch_max_len_dec))
In the original paper, sine and cosine function are used.
\[P_{p, \, i} = \begin{cases} \sin{(p/10000^{i/d})}, \quad \text{if i is even} \\ \cos{(p/10000^{(i-1)/d})}, \quad \text{if i is odd}\end{cases}\]If we use only one of the two funcitons, two word in far-apart positions can have the same encoding value because of the shape of the sin and cosine functions. Therefore, always use two of them.
The following is the implementation of the positional embedding.
class PositionalEncoding(tf.keras.layers.Layer):
def __init__(self, max_length, embed_size, dtype=tf.float32, **kwargs):
super().__init__(dtype=dtype, **kwargs)
assert embed_size % 2 == 0, "embed_size must be even"
p, i = np.meshgrid(np.arange(max_length), 2 * np.arange(embed_size // 2))
pos_emb = np.empty((1, max_length, embed_size))
pos_emb[0, :, ::2] = np.sin(p / 10000 ** (i / embed_size)).T
pos_emb[0, :, 1::2] = np.cos(p / 10000 ** (i / embed_size)).T
self.pos_encodings = tf.constant(pos_emb.astype(self.dtype))
self.supports_masking = True
def call(self, inputs):
batch_max_length = tf.shape(inputs)[1]
return inputs + self.pos_encodings[:, :batch_max_length]
All images, except those with separate source indications, are excerpted from lecture materials.

댓글남기기