심층 신경망 훈련 과정 문제
심층 신경망 훈련에서는 다음과 같은 문제를 마주할 수 있다.
- 출력 층에서 멀어질수록 gradient가 점점 작아지거나(vanishing gradient), 커지는 문제(exploding gradiet)가 나타날 수 있다. 이로 인해 하위 층의 훈련이 어려워진다.
- 훈련 데이터가 충분하지 않거나 레이블을 만드는 비용이 너무 많이 든다.
- 훈련이 극단적으로 느려진다.
- Overfitting의 위험이 커진다.
Vanishing Gradient, Exploding Gradient
심층 신경망에서 하위 층으로 갈수록 gradient가 점점 작아지는 현상을 vanishing gradient, 점점 커지는 현상을 exploding gradient라고 한다.
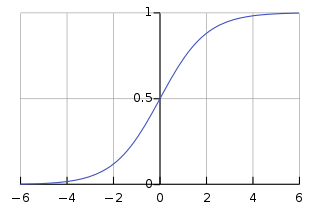
이처럼 gradient가 불안정해지는 주요 원인은 sigmoid 활성화 함수로, 각 층의 출력 분산이 입력보다 크기 때문이다. Sigmoid 함수는 입력의 절댓값이 클수록 gradient가 작아지기 때문에, 하위층으로 갈수록 전파할 gradient가 거의 남지 않는 상황이 생긴다.
Glorot Initialization
Vanishing gradient와 exploding gradient를 해결하기 위해서는 입력 분산과 출력 분산이 동일해야 한다. 그러나 입력 연결 개수(fan-in)과 출력 연결 개수(fan-out)가 동일하기는 어렵고, 이에 따라 분산이 완벽하게 동일하기란 매우 어려운 일이다. 대안으로, 각 층의 연결 가중치를 아래와 같이 랜덤으로 초기화할 수 있다. 저자의 이름을 따서 glorot initialization이라고 부른다.
\[\text{normal distribution, average is 0, variance is } \sigma^2 = \frac{1}{fan_{avg}}\\ \text{or when r=$\sqrt{\frac{3}{fan_{avg}}}$, unifrom distribution between -r and r}\]위 식의 다양한 변형이 있다.
| Initialization | Activation function | $\sigma^2$ |
|---|---|---|
| Glorot | No activation function, tanh, logistic, softmax | $\frac{1}{fan_{avg}}$ |
| He | ReLU, LeakyReLU, ELU, GELU, Swish, Mish | $\frac{2}{fan_{in}}$ |
| LeCun | SELU | $\frac{1}{fan_{in}}$ |
각 활성화 활성화 함수는 지정된 초기화 방식을 사용하였을 때 제대로 된 성능을 낼 수 있다.
keras는 기본적으로 균등 분포의 glorot 초기화를 사용한다. 그 변형을 사용하려면 다음과 같이 구현한다.
# one layer of He
import tensorflow as tf
dense = tf.keras.layers.Dense(50, activation='relu', kernel_initializer='he_normal')
# use fan_avg instead
he_avg_init = tf.keras.initializers.VarianceScaling(scale=2, mode='fan_avg',
distribution='uniform')
dense = tf.keras.layers.Dense(50, activation='sigmoid',
kernel_initializer=he_avg_init)
LeakyReLU
LeakyReLU는 다음과 같이 정의된다.
\[a = max(\alpha z, z)\]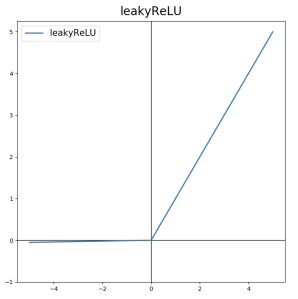
LeakyReLU는 z가 0보다 작을 때 gradient가 0이 되지 않으므로, 뉴런이 죽지 않고 다시 깨어날 가능성을 열어둔다는 의미가 있다.
$\alpha$ 가 새는 정도(leaky)를 결정한다. 보통 $\alpha$ 가 클 때 더 나은 성능을 낸다고 한다.
다양한 변형도 있다.
- RReLU(Randomized leaky ReLU): 훈련 시 주어진 범위에서 $\alpha$ 를 랜덤으로 선택하고, 테스트 시에는 평균 사용.
- PReLU(Parametric leaky ReLU): $\alpha$ 가 훈련하는 동안 학습된다.
Leaky ReLU 구현은 다음과 같이 한다. He 초기화를 사용해야 한다.
# one layer
leaky_relu = tf.keras.layers.LeakyReLU(alpha=0.2)
dense = tf.keras.layers.Dense(50, activation=leaky_relu,
kernel_initializer="he_normal")
# separete He and LeakyReLU
model = tf.keras.models.Sequential([
# [...] # other layers
tf.keras.layers.Dense(50, kernel_initializer="he_normal"), # no activation function
tf.keras.layers.LeakyReLU(alpha=0.2), # LeakyReLU
# [...] # other layers
])
ELU, SELU
ReLU, LeakyReLU, PReLU는 모두 매끄러운 함수가 아니다. 즉, 도함수가 0에서 갑자기 바뀌며, 경사 하강법이 최적점에서 진동하거나 수렴을 느리게 할 수 있다.
위 문제를 해결한 ELU(Exponential Linear Unit)와 SELU(Scaled ELU)를 살펴보자.
먼저 ELU는 다음과 같다.
\[\text{ELU}_{\alpha}(z)=\begin{cases} \alpha(e^z - 1), & \text{if $z<0$}.\\ z, & \text{if $z \geq 0$}. \end{cases}\]ElU는 계산이 느리다는 단점이 있다.
SELU는 스케일이 조정된 ELU라고 보면 되는데, $\alpha \approx 1.67$ 이고 ELU의 약 1.05배이다. SELU로 모든 층을 구성한다면 신경망이 자기 정규화의 특성을 가지고 아주 깊은 신경망에서 높은 성능을 낸다.
하지만 SELU는 제약도 많다. 입력 특성을 반드시 standardization해야 한다. 또한 일반적인 신경망에서만 작동하며, 스킵 연결(e.g. Wide & Deep) 등에서는 잘 작동하지 않는다. $l_1$, $l_2$ 규제, 드롭 아웃, 배치 정규화, max-norm 같은 규제도 사용할 수 없다.

keras에서 ELU와 SELU를 사용하려면 activation="elu" 또는 activation="selu"로 지정한다.
GELU, Swish, Mish
GELU 역시 ReLU의 매끄러운 변형이다. GELU는 다음과 같이 정의된다.
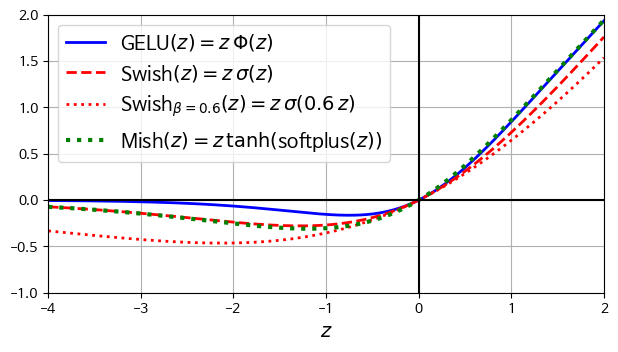
\[\text{GELU}(z) = z \Phi(z)\]$\Phi$ 는 표준 가우스 누적 분포 함수로, $\Phi(z)$ 는 평균이 0이고 분산이 1인 정규 분포에서 랜덤하게 샘플링한 값이 z보다 작을 확률에 해당한다.
GELU는 0보다 작은 구간에서 일관되게 증가하는 것이 아니라 아래로 구부러지며 저점에 도달했다가 증가하는 모양을 하고 있다. 이러한 복잡한 모양 덕분에 복잡한 패턴을 학습하기 좋다. 물론 계산량은 좀 더 늘어난다.
시그모이드 $\sigma$ 를 사용하면 $z \sigma(1.702z)$ 로 근사할 수 있으며, 계산이 훨씬 빠르다.
일반화 된 Swish는 $z \sigma(z)$ (SiLU, swish)를 일반화한 것으로 보면 된다.
\[\text{Swish}_{\beta}(z) = z \sigma (\beta z)\]$\beta=1.702$ 라면 GELU와 거의 동일하다. $\beta$ 역시 경사 하강법으로 훈련할 수 있는 파라미터이다.
Mish는 매우 비슷한 모습을 하고 있다.
\[\text{Mish}_{\beta}(z) = z \tanh (\text{softplus}(z))\]keras에서는 GELU와 swish를 지원하므로, activation="gelu", activation="swish"로 지정하면 된다. 하지만 Mish나 일반화 된 swish는 아직 지원하지 않는다.
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기