퍼셉트론
퍼셉트론(Perceptron)은 가장 간단한 인공 신경망 구조이다. 퍼셉트론은 TLU(Threshold Logic Unit)라고 불리는 인공 뉴런을 기반으로 한다.
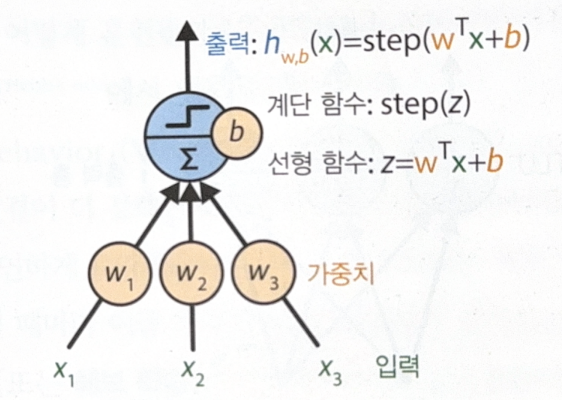
입력의 선형 함수를 먼저 계산하고, 그 다음에 그 결과에 계단 함수(step function)를 적용한다. 계단 함수는 다음과 같다.

계단 함수는 역전파와 경사 하강법에서 한계를 드러내며, 다양한 활성화 함수로 대체된다.
퍼셉트론은 하나의 층 안에 놓인 하나 이상의 TLU로 구성되며, 각 TLU는 모든 입력에 연결된다. 이를 완전 연결 층(fully connected later) 혹은 밀집 층(dense layer)라고 한다. 구조를 시각화하면 다음과 같다.
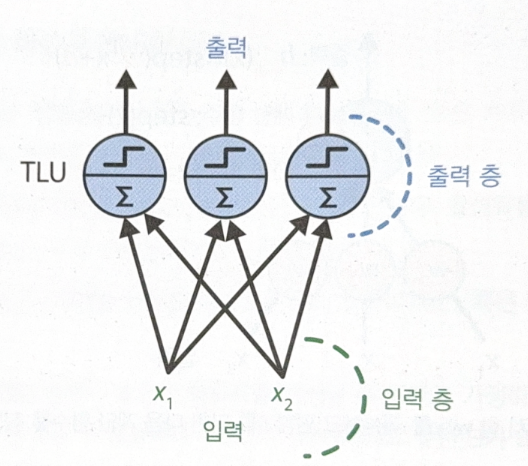
벡터화를 적용한 완전 연결층의 출력 계산식은 다음과 같다.
\[h_{W, b} = \phi(XW + b)\]퍼셉트론 학습 규칙은 다음과 같다.
\[w_{i, j}^{next \; step} = w_{i, j} + \eta(y_i - \hat{y}_i)x_i\]$w_{i, j}$ 는 i번째 입력 뉴런과 j번째 출력 뉴런 사이를 연결하는 가중치이다. 실제 값과 예측 값 간의 차이에 학습률 $\eta$ 를 이용해 가중치를 업데이트 한다.
퍼셉트론 학습을 다음과 같이 구현할 수 있다.
import numpy as np
from sklearn.datasets import load_iris
from sklearn.linear_model import Perceptron
iris = load_iris(as_frame=True)
X = iris.data[['petal length (cm)', 'petal width (cm)']].values
y = (iris.target == 0)
per_clf = Perceptron()
per_clf.fit(X, y)
y_pred = per_clf.predict([[2, 0.5], [3, 1]])
y_pred
다른 강의에서 살펴보았지만, 퍼셉트론은 XOR 문제를 풀 수 없다는 치명적인 단점을 가지고 있다.
이는 퍼셉트론을 여러 개 쌓아올린 다층 퍼셉트론(MLP)으로 해결할 수 있다.
MLP와 역전파
MLP의 구조는 다음과 같다.
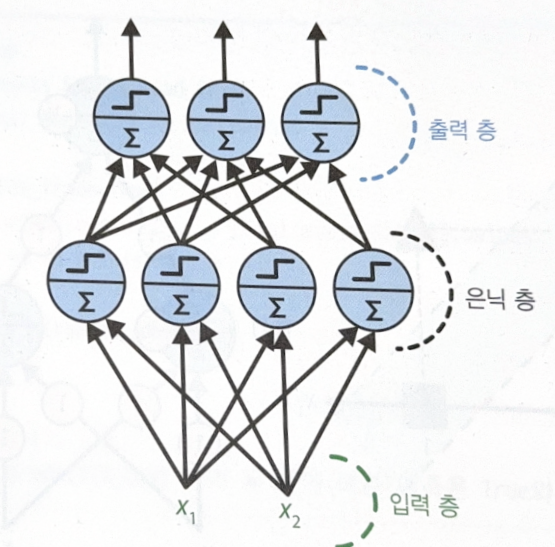
은닉층이 여러 개 있는 것을 심층 신경망(Deep Neural Network, DNN)이라고 한다.
심층 신경망은 역전파(backpropagation)를 통해서 훈련할 수 있다. 신경망을 훈련하는 과정은 크게 3단계로 구성된다.
- 정방향 계산: 예측 생성.
- 역방향 계산: 역방향으로 진행하며 각 연결이 오차에 기여한 정도 측정.
- 경사 하강법: 연결 가중치 업데이트.
세부적으로 보면 다음과 같다.
- 입력을 이용해 출력을 계산. 역전파를 위해 중간 계산 값을 저장한다.
- 네트워크의 출력 오차를 측정한다(손실 함수를 이용해 기대하는 출력과 실제 출력을 비교하고 오차 측정값을 반환한다).
- 각 출력의 오차와 출력 층의 각 연결이 2의 오차에 얼마나 기여했는지 계산한다. 연쇄 법칙(chain rule)이 이용된다.
- 이전 층의 연결 가중치가 이 오차의 기여 정도에 얼마나 기여했는지(쉽게 말하면 이전 층의 책임이 어느 정도인지) 측정한다. 연쇄 법칙이 이용된다.
- 4를 계속 반복하여 입력층까지 간다.
- 경사 하강법을 수행하여 신경망 내의 모든 연결 가중치를 수정한다.
3~5의 과정에서 역전파라는 이름이 유래되었다.
다양한 활성화 함수
초기 퍼셉트론에서는 계단 함수가 사용되었지만, 계단 함수는 수평선 구조밖에 없어 경사 하강법에서 경사를 계산할 수 없다. 이를 보완하기 위해 시그모이드 함수, tanh 함수, ReLU 함수 등이 사용되고 있다.
활성화 함수가 필요한 이유는 비선형성을 추가하기 위해서이다. 층 사이에 비선형성을 추가하지 않으면 아무리 층을 쌓아도 하나의 층과 동일해지며(선형 함수 2개를 합성하면 선형 함수가 도출된다), 이는 복잡한 문제를 풀 수 없게 한다.
MLP 회귀
회귀 문제를 풀 때 우리가 원하는 예측 값이 여러 개라면 그 수만큼의 출력 뉴런이 있어야 한다.
사이킷런에서는 MLPRegressor를 이용해 MLP 회귀를 할 수 있다. 경사 하강법을 사용하기 때문에 특성 스케일링이 꼭 필요하다.
from sklearn.datasets import fetch_california_housing
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.neural_network import MLPRegressor
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
housing = fetch_california_housing()
X_train_full, X_test, y_train_full, y_test = train_test_split(housing.data, housing.target, random_state=42)
X_train, X_valid, y_train, y_valid = train_test_split(X_train_full, y_train_full, random_state=42)
mlp_reg = MLPRegressor(hidden_layer_sizes=[50, 50, 50], random_state=42)
pipeline = make_pipeline(StandardScaler(), mlp_reg)
pipeline.fit(X_train, y_train)
y_pred = pipeline.predict(X_valid)
rmse = mean_squared_error(y_valid, y_pred, squared=False)
만약 출력이 항상 양수임을 보장하고 싶다면 ReLU나 softplus 함수를 출력 층에 사용하면 된다. 하지만 MLPRegressor는 출력 층에서 활성화 함수를 지원하지 않는다.
기본적으로 MLPRegressor는 평균 절대 오차(MSE)를 지원하지만, train set에 이상치가 많다면 평균 절대 오차 대신 후버 손실(huber loss)을 사용하는 것이 더 낫다. 하지만 MLPRegressor는 후버 손실도 지원하지 않는다. 어쩌라는 겨 keras 쓰지
다음은 MLP 회귀에서의 전형적인 신경망 구조이다.
| 하이퍼파라미터 | 일반적인 값 |
|---|---|
| 은닉 층 수 | 문제에 따라 다름(1~5) |
| 은닉 층의 뉴런 수 | 문제에 따라 다름(10~100) |
| 출력 뉴런 수 | 예측 차원마다 하나 |
| 은닉 층의 활성화 함수 | ReLU |
| 출력 층의 활성화 함수 | 없음, ReLU/softplus(출력이 양수일 때), logistic/tanh(출력을 특정 범위로 제한할 때) |
| 손실 함수 | MSE, 후버(이상치가 있을 때) |
MLP 분류
분류 문제에서의 출력 뉴런 수는 문제의 종류마다 다르다. 이항 분류면 1개, 다중 분류 혹은 다중 레이블 분류면 여러 개가 필요할 것이다.
각 샘플이 여러 개의 클래스 중 하나의 클래스에만 속할 수 있다면 출력 층에는 softmax 활성화 함수를 사용한다. 이는 모든 예측 확률을 0과 1사이로 만들고 모든 클래스의 확률을 더했을 때 1이 되도록 한다.
손실 함수에는 크로스 엔트로피를 이용한다.
MLP 분류의 전형적인 구조는 다음과 같다.
| 하이퍼파라미터 | 이진 분류 | 다중 레이블 분류 | 다중 분류 |
|---|---|---|---|
| 은닉 층 수 | 문제에 따라 다름 | 문제에 따라 다름 | 문제에 따라 다름 |
| 출력 뉴런 수 | 1개 | 이진 레이블마다 1개 | 클래스마다 1개 |
| 출력 층의 활성화 함수 | sigmoid | sigmoid | softmax |
| 손실 함수 | cross-entropy | cross-entropy | cross-entropy |
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기