[Deep Learning Specialization - 4단계] 6. 신경망 스타일 변형

신경망 스타일 변형

신경망 스타일 변형은 신경망을 이용해 그림의 스타일을 변형하는 것을 말한다.

위 예시처럼 우리가 변형하고자 하는 이미지(C)를 원하는 스타일(S)로 변형하여 결과(G)가 도출된다.

합성곱 신경망 층의 깊이에 따라 보는 것이 달라진다

합성곱 신경망은 더 깊은 층으로 갈수록 더 복잡한 이미지를 본다. 예를 들어 초반 층에서는 주황색, 비스듬한 선을 본다면, 깊은 층에서는 사람의 얼굴, 자동차 바퀴 같은 이미지를 보는 식이다.

비용함수

컨텐츠 이미지(C), 스타일 이미지(S), 결과 이미지(G)가 있을 때, 비용함수는 다음과 같이 정의한다.

\[J(G) = \alpha J_{content}(C, G) + \beta J_{style}(S, G)\]

$J_{content}(C, G)$ 는 C와 G의 유사한 정도를, $J_{style}(S, G)$ 는 S와 G의 유사한 정도를 나타낸다. $\alpha$, $\beta$ 는 가중치이다.

새로운 이미지 G를 찾아내는 방법은 다음과 같다.

1. 랜덤한 이미지 G를 생성
2. 경사하강법으로 $J(G)$ 를 최소화 ($G = G - \frac{\partial}{\partial G}J(G)$)

새로운 이미지 G를 찾는 과정. 처음에는 랜덤한 이미지였다가, 경사하강법에 의해 점점 S와 유사한 스타일을 가지는 것을 확인할 수 있다.

컨텐츠 비용함수

$J(G)$ 의 식에서 컨텐츠 비용함수($J_{content}(C, G)$)를 더 자세히 살펴보자.

너무 얕거나 깊지도 않은 특정한 은닉 층($l$)을 생각한다. (여기서는 이미 훈련된 합성곱 신경망을 사용한다.) $a^{l}$, $a^{l}$ 는 각각 $l$ 층의 활성화 값이다. 만약 이 두 값이 비슷하다면, 두 이미지(C, G)는 유사한 컨텐츠를 가진다고 보면 된다.

\[J_{content}(C, G) = \frac{1}{2} ||a^{[l](C)} - a^{[l](G)}||^2\]

$\frac{1}{2}$ 은 정규화를 위한 것으로, 크게 신경쓸 필요 없다.

스타일 비용함수

이번엔 스타일 비용함수($J_{style}(S, G)$)를 자세히 보자.

여기서도 $l$번째 층을 사용한다. 각 층에서 스타일은 서로 다른 채널의 활성화 값 간 상관 관계라고 정의한다. 아래 그림을 참고하자.

출처: 네이버 부스트코스

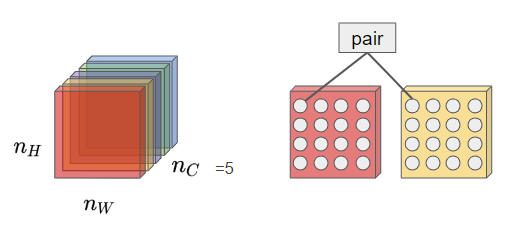
서로 다른 채널의 활성화 값의 상관관계가 무엇을 의미할까? 상관관계가 크다면 두 요소가 동시에 나타나는 것을, 작다면 두 요소는 동시에 나타나지 않는다는 것을 의미한다. 아래 그림을 예로 들어보자.

맨 윗 줄 가운데 뉴런과 가운데 줄 가장 왼쪽 뉴런이 상관관계가 크다고 해보자. 이는 주황색 색조와 수직 선이 동시에 나타나는 상황이 많다는 것을 의미한다.

$a^{[l]}_{i, j, k}$ 를 (i. j, k)에서의 활성화 값이라고 해보자.(i, j, k는 각각 높이, 너비, 채널에서의 위치) $G ​^{[l]} \, (n_c^{[l]} \times n_c^{[l]})$ 는 $l$ 층에서 스타일 이미지에 대한 상관 관계 행렬을 계산한 것이다. 이를 스타일 행렬이라고 한다.

스타일 행렬 각각의 요소는 다음과 같이 계산된다.

$\displaystyle G_{kk’}^{[l] (S)} = \sum_{i=1}^{n_H^{[l]}} \sum_{j=1}^{n_W^{[l]}}{a^{[l] (S)}{i, j, k} a^{[l] (S)}{i, j, k’}}$

$\displaystyle G_{kk’}^{[l] (G)} = \sum_{i=1}^{n_H^{[l]}} \sum_{j=1}^{n_W^{[l]}}{a^{[l] (G)}{i, j, k} a^{[l] (G)}{i, j, k’}}$

$l$번째 층에서 스타일 비용함수는 다음과 같이 정의된다.

\[\displaystyle J_{style}^{[l]} (S, G) = \frac{1}{(2n_H^{[l]}n_W^{[l]}n_C^{[l]})^2} ||G^{[l] (S)} - G^{[l] (G)}||_F^2 \\ = \frac{1}{(2n_H^{[l]}n_W^{[l]}n_C^{[l]})^2} \sum_{k} \sum_{k'}{(G_{kk'}^{[l] (S)} - G_{kk'}^{[l] (G)})^2}\]

$\frac{1}{(2n_H^{[l]}n_W^{[l]}n_C^{[l]})^2}$ 는 정규화 상수로, 크게 신경쓸 필요 없다.

전체 스타일 비용함수는 다음과 같다.

\[\displaystyle J_{style}(S, G) = \sum_{l}{\lambda^{[l]} J_{style}^{[l]} (S, G)}\]

$\lambda^{[l]}$ 는 초매개변수로 신경망의 다른 층을 사용하는 것을 허용하는 것이다.

식이 많았으니 과정을 요약해보자. 먼저, 우리는 스타일 이미지(S)의 요소들이 어떤 상관관계를 가지는지를 분석해서, 그것을 S의 스타일이라고 정의했다. 그리고 이 정의 그대로 S와 G의 스타일을 계산하고, 그 차이를 점점 줄여나가기로 한 것이다.

1D와 3D 이미지에도 적용하기

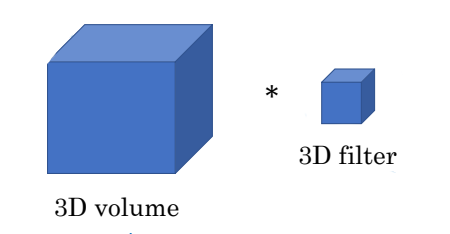
1차원과 3차원 이미지에도 이러한 합성곱 신경망을 적용할 수 있다. 방법은 2차원 이미지와 동일하다.

특히 요즘은 CT, MRI 등의 의료 기술이 발달하면서 3차원 이미지 분석도 중요해지고 있다. 3차원 이미지 예시를 하나 보자.

별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.