얼굴 인식
얼굴 검증(face verification)과 얼굴 인식(face recognition)은 다르다.
얼굴 검증은 이미지와 이름(ID)를 입력 받아 이미지가 그 사람에 해당하는지 여부를 도출한다.
반면, 얼굴 인식은 k명의 사람에 대한 데이터베이스를 가지고 있으며, 입력 이미지를 받아 그 이미지가 데이터베이스에 있을 경우 해당하는 사람의 ID를 도출한다.
얼굴 검증보다는 얼굴 인식이 더 복잡하다.
원 샷 학습
원 샷(One-shot) 학습 문제는 얼굴 인식 시스템이 하나의 예시 이미지만 가지고 사람을 판별해야 하는 문제를 의미한다. 보통 시스템에 얼굴을 등록할 때는 사진 하나만 등록하는 경우가 많기 때문에, 이 이미지 하나만 가지고 얼굴을 파악해야하는 것이다.
접근 방법 중 하나는 출력 시 직원과 모르는 사람이라는 클래스를 softmax 유닛으로 추가해서 학습시키는 것이다. 하지만 이는 신경망을 훈련시키기에 충분하지 않기도 하고, 새로운 사람이 입사하게 되면 소프트맥스 유닛을 추가해서 다시 훈련시켜야 한다는 문제점이 있다.
대신 유사도 함수를 학습시키는 방법이 있다. 유사도 함수는 다음과 같이 정의된다.
$d(img1, \, img2)$ = degree of difference between images
위 값이 어떤 역치($\tau$)보다 작으면 동일한 인물이고, 그렇지 않으면 다른 인물인 것으로 판단할 수 있다.
유사도 함수를 사용하면 다른 사람이 추가되더라도 쉽게 판별할 수 있다.
샴 네트워크
어떤 이미지를 합성곱 신경망에 넣어서 얻은 결과를 $f(x^{(1)})$ ($x^{(1)}$ 의 인코딩)라 하자. 그리고 또 다른 이미지를 같은 합성곱 신경망에 독립적으로 넣어서 얻은 결과를 $f(x^{(2)})$ 라 해보자. 두 벡터 사이의 거리(norm)는 다음과 같이 표현할 수 있다.
\[d(x^{(1)}, x^{(2)}) = ||f(x^{(1)}) - f(x^{(2)})||_2^2\]이처럼 두 개의 입력에 대해 독립적으로 두 개의 합성곱 신경망을 실행한 뒤 비교하는 것을 샴 네트워크(Siamese network)라고 한다.
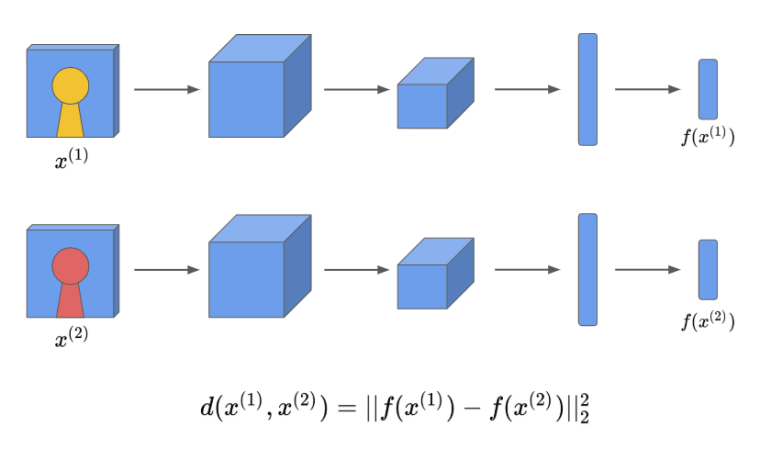
샴 네트워크의 학습 순서를 정리하면 다음과 같다.
- 신경망의 변수들이 $x^{(i)}$ 의 인코딩을 정의한다.
- $x^{(i)}$, $x^{(j)}$ 가 같은 사람이면 둘의 거리를 작게, 다른 사람이면 둘의 거리가 커지도록 변수를 학습한다.
삼중항 손실이란?
기준이 되는 이미지를 Anchor(A), A와 같은 이미지를 Positive(P), 다른 사람의 이미지를 Negative(N)라 해보자.

우리가 원하는 것은 A와 P 사이의 거리가 A와 N 사이의 거리보다 작아지도록 학습하는 것이다. 이를 식으로 작성하면 다음과 같다.
\[||f(A) - f(P)||^2 \leq ||f(A) - f(N)||^2\]한 가지 생각해볼 점이 있다. 극단적이지만 만약 신경망이 A, P, N의 차이가 아예 없는 것으로 학습하면 어떻게 될까? 아니면 $f(A)$. $f(P)$, $f(N)$ 이 모두 0이라고 학습한다면? 곤란한 상황이 생길 것이다. 이처럼 너무나 자명한 해를 내놓는 것을 방지하기 위해 margin($\alpha$)를 식에 추가한다.
보통 아래처럼 한 쪽으로 이항해서 표현한다.
\[||f(A) - f(P)||^2 - ||f(A) - f(N)||^2 + \alpha \leq 0\]삼중항 손실에서의 손실, 비용함수
손실함수를 정의해보자. A, P, N 3개의 이미지가 주어졌을 때, 손실함수는 다음과 같이 표현된다.
\[L(A, \, P, \, N) = max(||f(A) - f(P)||^2 - ||f(A) - f(N)||^2 + \alpha, \, 0)\]만약 앞쪽이 0보다 크다면(신경망이 제대로 학습되지 않은 경우) 우리는 그 값을 손실함수의 결과로 선택한다. 그러나 앞이 0보다 작다면(신경망이 제대로 학습된 경우), 우리는 손실함수의 값을 0으로 한다. (앞쪽 식의 계산 결과는 신경쓰지 않는다.)
손실함수로부터 비용함수도 정의할 수 있다.
\[J = \sum_{i=1}^{m}{L(A^{(i)}, \, P^{(i)}, \, N^{(i)})}\]이 신경망을 처음 학습할 때는 1천명에 대해 각 10개의 이미지, 즉 1만개 이상의 이미지가 필요하다. 그러나 한 번 제대로 학습하고 나면 원 샷 학습 문제처럼 1개의 예시만으로도 얼굴 인식을 할 수 있다.
삼중항 손실에서 A, P, N 선택하기
A, P, N을 선택하는 과정을 생각해보자. 만약 랜덤하게 선택한다면 A, P는 매우 유사하고, A, N은 매우 다른 이미지가 선택될 것이다. 이는 \(d(A, \, P) + \alpha \leq d(A, \, N)\) 을 너무 쉽게 만족시킬 것이고, 경사하강법의 적용이 힘들 것이다. 결과적으로 제대로 얼굴 구분을 해내지 못하는 엉망인 신경망이 개발된다.
따라서 A, P, N을 선택할 때는 학습하기 어려운 예시들($d(A, \, P) \approx d(A, \, N)$인 것)로 골라서, 경사하강법을 통해 신경망이 제대로 학습되도록 할 필요가 있다.
얼굴 검증 및 이진 분류
샴 네트워크를 이용해서 두 이미지가 같은지 아닌지를 판별하는 다른 방법은 신경망의 마지막에 로지스틱 회귀를 사용해서 결과를 0 또는 1로 만드는 것이다. 1이면 같은 사람, 0이면 다른 사람이다.
로지스틱 회귀를 적용한 식은 다음과 같이 표현할 수 있다.
\[\hat{y} = \sigma(\sum_{k=1}^{128}{w_i |f(x^{(i)})_k - f(x^{(j)})_k|} + b)\]이를 통해서 이진 분류를 할 수 있게 된다. 여러 이미지 묶음을 만든 뒤, 이미지가 같은 사람이면 1, 다른 사람이면 0으로 정답을 제공하면 된다.
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기