1 x 1 합성곱
1 x 1 합성곱은 언뜻 보기에 큰 의미가 없어보인다. 그냥 입력 층의 모든 요소들에 같은 수를 곱해주는 것이기 때문이다. 그러나 실제로 1 x 1 합성곱은 매우 유용하게 사용된다. 특히 입력이 여러 개의 채널을 가지고 있을 때 그 효과가 발휘된다.
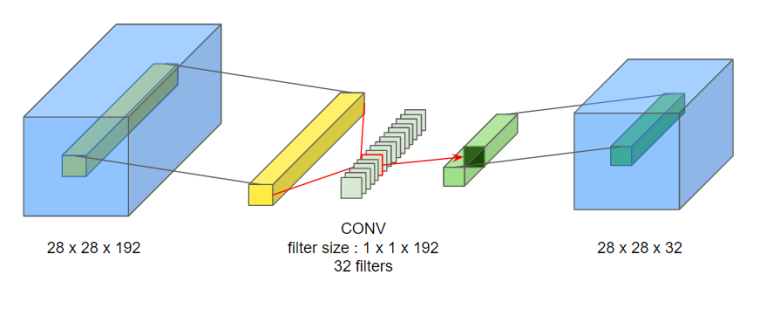
왼쪽의 28 x 28 x 192 입력이 1 x 1의 크기를 가진 필터 32개로 합성곱되어 28 x 28 x 32의 출력이 되었다. 이처럼 1 x 1 합성곱은 채널의 개수를 줄이는 데 사용된다.
인셉션 신경망 - 기본 아이디어
필터의 크기나 풀링을 어떻게 정하는 것이 가장 좋을지 망설여진다면 인셉션 신경망(Inception Network)를 사용할 수 있다. 인셉션 신경망은 필터의 크기나 풀링을 결정하는 대신 전부 다 적용해서 출력들을 합치고, 신경망으로 하여금 스스로 변수나 필터 크기의 조합을 학습하게 만드는 것이다.
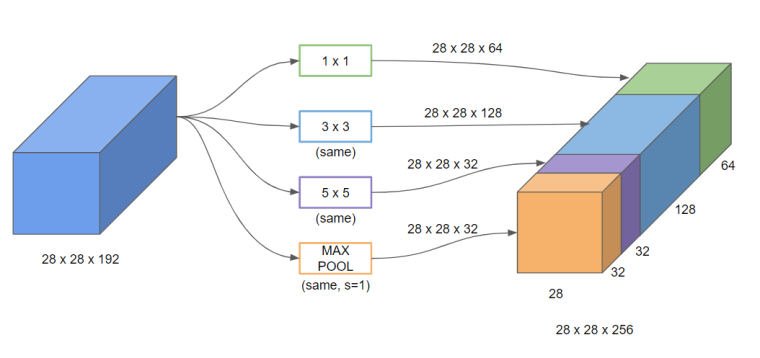
그럼 아마 여기서 ‘그 많은 계산을 다 해야 한다고? 과연 그게 효율적일까?’라는 의문이 들 것이다. 그렇다. 인셉션 신경망에서 가장 신경써야할 부분은 아마 계산 비용일 것이다. 마침 이 계산 비용을 줄일 수 있는 방법이 있다.
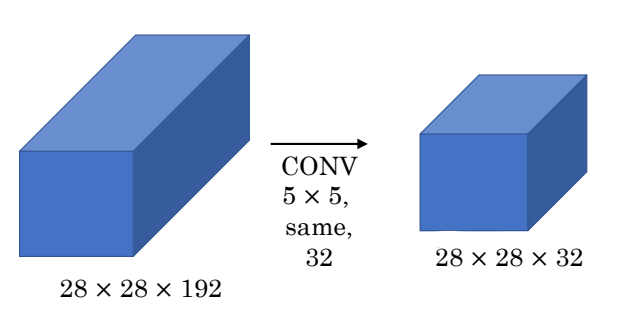
위 그림과 같은 합성곱에서 몇 번의 계산이 필요한지 구해보자. $28 \times 28 \times 32 \times 5 \times 5 \times 192$ 의 과정으로 총 1억 2000만번의 계산이 필요하다.
그런데 중간에 1 x 1 합성곱을 한 번 추가하면 이야기가 달라진다.
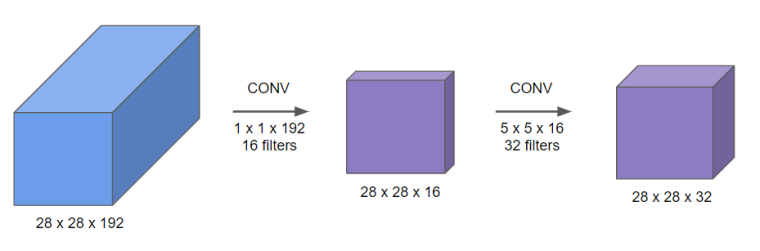
첫 단계에서 계산 횟수는 $28 \times 28 \times 16 \times 1 \times 1 \times 192$ 로 240만번, 두 번째 단계에서는 $28 \times 28 \times 32 \times 5 \times 5 \times 16$ 으로 1000만번이다. 둘을 더하면 총 계산은 1240만번으로, 단계를 나누기 전보다 계산이 확 줄어드는 것을 볼 수 있다. 이처럼 1 x 1 합성곱을 적용하는 단계(병목층)를 한 번 추가하여 계산 비용을 감소시킬 수 있다.
인셉션 신경망 - 구현하기
앞서 인셉션 신경망의 기본 아이디어를 설명하면서 사용한 그림을 신경망의 한 단계(인셉션 모듈)처럼 표현해보았다.
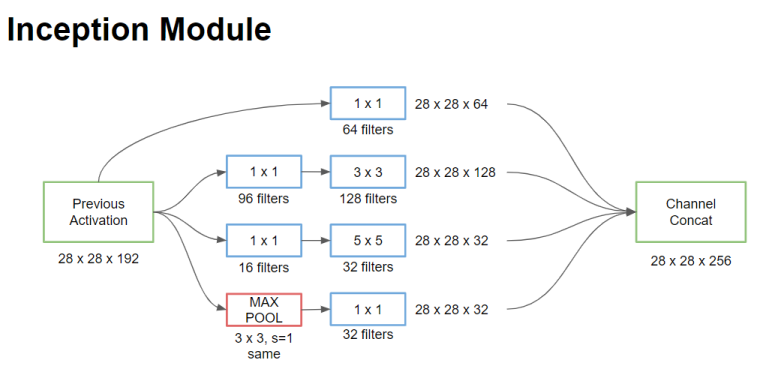
가장 위쪽부터 살펴보자. 1 x 1 합성곱만 적용한 부분이 보인다. 그 바로 아래에는 1 x 1 합성곱을 적용한 다음 3 x 3 합성곱을 적용하였다. 다음은 1 x 1 합성곱을 적용한 다음 5 x 5 합성곱을 적용하였다. 마지막이 조금 특이한데, 최대 풀링 이후 1 x 1 합성곱을 적용한 것을 확인할 수 있다. 여기서는 풀링임에도 입력의 너비와 높이를 유지시킨 것이 눈에 띈다.
위 인셉션 모듈을 연속적으로 적용해 인셉션 신경망을 만들 수 있다.
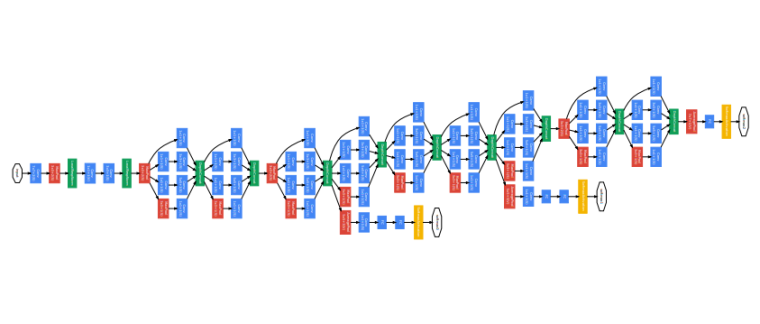
위 인셉션 신경망은 구글의 일원이 개발했다고 하여 googLeNet이라고도 부른다(LeNet을 기리기 위한 표현이기도 하다). 중간 중간 신경망이 끝나지 않았음에도 softmax로 예측값을 도출하는 부분들이 보이는데, 이는 중간에 도출된 결론이라도 꽤 쓸만하다는 사실을 나타낸다.
재미로, ‘인셉션’이라는 이름은 레오나르도 디카프리오 주연의 그 영화에서 따온 것이 맞다. 디카프리오의 “We need to go deeper”라는 대사는, 신경망과 연결지어보면 참 묘하다.
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기