합성곱 신경망 한 층 구성하기
합성곱 신경망의 한 층을 구성하는 과정은 지금까지 신경망을 구성했던 것과 유사하다. 먼저 (1)합성곱 연산을 한 뒤, (2) 편향(b)을 더해주고, (3) 활성화 함수에 넣어 결과(다음 입력값)를 도출한다.
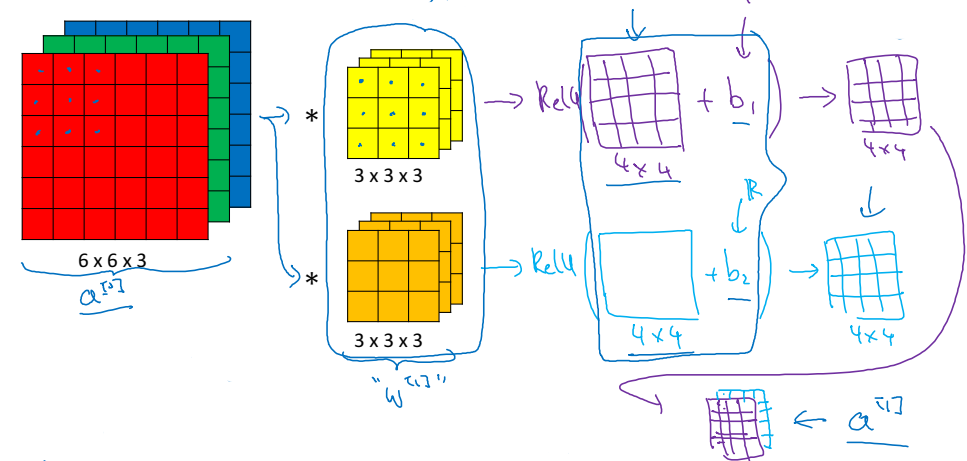
신경망의 한 층에서 사용되는 매개변수는 몇 개일까? 필터에 사용되는 매개변수와 편향 매개변수의 개수를 더하면 구할 수 있다. 예를 들어, (3 x 3 x 3)의 넓이를 가진 필터 10개를 사용했다면 $(3 \times 3 \times 3 + 1) \times 10$가 되어 280개의 매개변수가 사용되었을 것이다.
합성곱 신경망 한 개의 층에서 사용되는 표현들에 대해 정리하면 다음과 같다.
| 항목 | 표현 |
|---|---|
| 필터의 크기 | $f^{[l]}$ |
| 패딩 | $p^{[l]}$ |
| 스트라이드 | $s^{[l]}$ |
| 필터의 개수 | $n_c^{[l]}$ |
| 입력의 넓이 | $n_H^{[l-1]} \times n_W^{[l-1]} \times n_c^{[l-1]}$ |
| 출력의 넓이 | $n_H^{[l]} \times n_W^{[l]} \times n_c^{[l]}$ |
| 각 필터의 넓이 | $f^{[l]} \times f^{[l]} \times n_c^{[l]}$ |
| 활성화 함수 결과의 넓이 | $a^{[l]} \rightarrow n_H^{[l]} \times n_W^{[l]} \times n_c^{[l]}$ |
| 가중치의 넓이 | $f^{[l]} \times f^{[l]} \times n_c^{[l-1]} \times n_c^{[l]}$ |
| 편향 | $n_c^{[l]}$ |
| $l$번째 층의 높이 혹은 넓이 | $n_H^{[l]} = \lfloor \frac{n_W^{[l-1]}+2p^{[l]}-f^{[l]}}{s^{[l]}} + 1 \rfloor$ |
| 벡터화된 활성화 함수 결과 | $A^{[l]} \rightarrow m \times n_H^{[l]} \times n_W^{[l]} \times n_c^{[l]}$ |
간단한 합성곱 신경망 예시
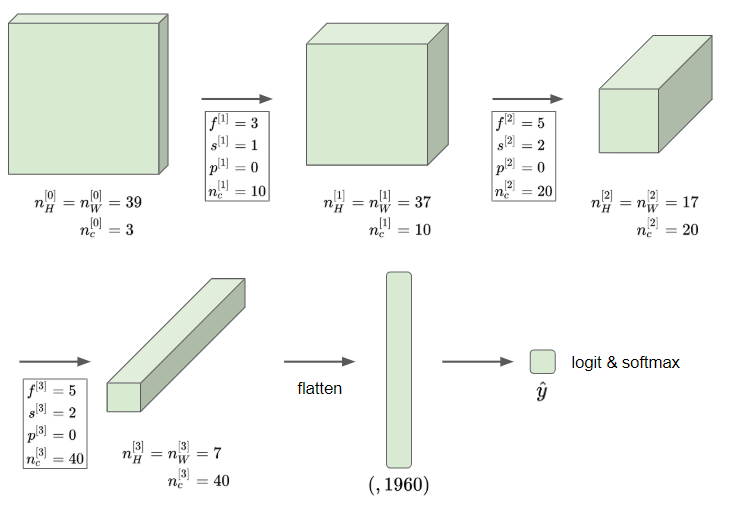
위 그림은 간단한 합성곱 신경망의 한 예시이다. 처음 과정만 자세히 파헤쳐 보자. (39 x 39 x 3)의 넓이를 가진 사진을 입력흐로 하고, 필터의 크기는 3, 스트라이드는 1, 패딩은 0으로 하였다. 또한, 필터는 10개를 사용하였다. 다음과 같은 계산을 통해 다음 층의 입력값에 대한 정보를 구한다.
$n_H^{[1]} = \lfloor \frac{n_W^{[0]}+2p^{[1]}-f^{[1]}}{s^{[1]}} + 1 \rfloor = \lfloor \frac{39+2 \times 0-3}{1} + 1 \rfloor = 37$
따라서 다음 신경층의 입력은 (37 x 37 x 10)의 넓이를 가지게 된다. 같은 과정을 계속해서 반복하여 마지막에 (7 x 7 x 10)의 넓이를 가진 이미지를 구하였다.
마지막 마무리는 로지스틱 회귀나 softmax 회귀를 사용한다. 이를 위해서 $7 \times 7 \times 10=1960$개의 요소들을 펼쳐서 (1960, 1)의 벡터를 만든다. 그리고 회귀를 사용하여 최종 예상 값을 도출하는 것이다.
풀링 층
합성곱 신경망에서는 풀링(Pooling) 층을 사용해 표현의 크기를 줄임으로써 계산속도를 줄이고 특징을 더 잘 검출할 수 있다.
대표적인 풀링에는 최대 풀링이 있다.

왼쪽의 이미지를 최대 풀링 해보자. 먼저, 이미지를 (2 x 2)의 4개 부분으로 쪼갠다. 그리고 각 구역의 최댓값을 그 구역의 대푯값으로 삼는 것이다. 그럼 오른쪽과 같은 결과 이미지(2 x 2)를 구할 수 있다.
최대 풀링을 필터로 이해할 수도 있다. 위의 경우 필터의 크기(f)가 2이며, 스트라이드(s)가 2인 상황으로 이해할 수 있다.
평균 풀링도 있다. 이름에서 유추할 수 있듯이 최댓값이 아닌 평균값을 사용하는 것이다. 그러나 현실에서는 최대 풀링을 더 많이 사용한다.
풀링에서의 초매개변수라고 한다면 필터의 크기(f)와 스트라이드(s), 그리고 최대 풀링인지, 평균 풀링인지 여부를 들 수 있다. 풀링에서 주의할 것은 합성곱에서와는 다르게 학습해서 구할 수 있는 매개변수가 없다는 사실이다.
복잡한 합성곱 신경망 예시
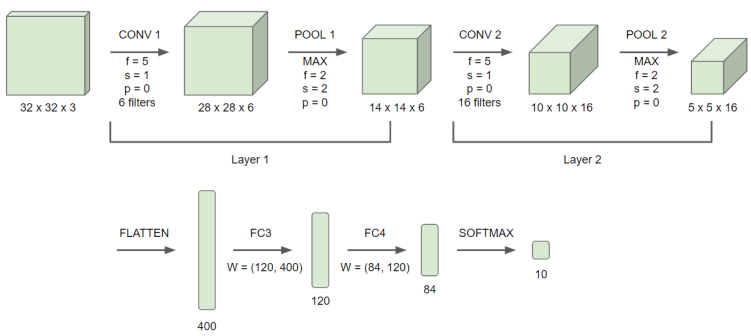
이제 복잡한 합성곱 신경망도 한 번 보자. 간단한 합성곱 신경망과 다른 점은 합성곱 층(CONV)만을 사용한 것이 아니라 풀링 층(POOL), 완전 연결 층(FC)도 사용했다는 사실이다.
위 신경망에 대해 몇 가지 짚고 넘어갈만한 사실들이 있다.
- LeNet-5라는 신경망에서 영감을 얻었다.
- 매개변수와 가중치가 있는 층만을 하나의 층으로 인정한다. 즉, 풀링 층의 경우 초매개변수만 있기 때문에 합성곱 층과 합쳐서 하나의 층으로 인정한다.
- CONV - POOL - CONV - POOL - FC - FC - FC - Softmax 처럼 합성곱 층, 풀링 층이 번갈아 나오다가 완전 연결 층이 연달아 나오고 softmax 회귀로 마무리하는 패턴이 흔하다.
위 예시에 대해 정리하면 다음과 같다.
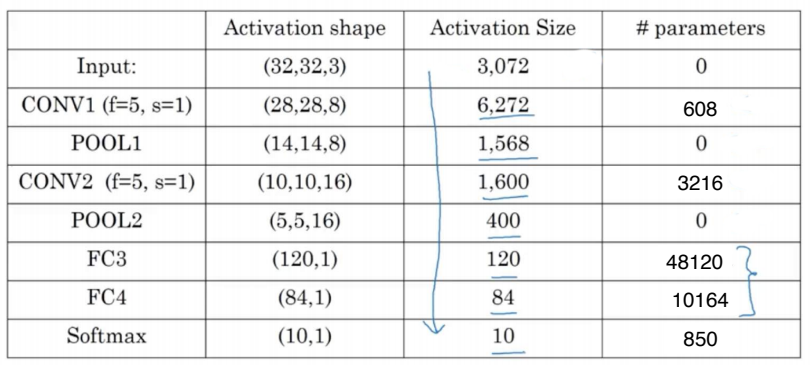
위 표로부터 합성곱 신겸망의 중요한 사실을 얻어보자.
- 활성화 값의 크기가 신경망이 깊어질 수록 점점 감소한다.
- 완전 연결 층에 비해 합성곱 층의 매개변수가 압도적으로 적고, 풀링 층의 매개변수는 없다.
왜 합성곱인가?
왜 합성곱 신경망인가? 일단 매개변수의 수가 적어서 도움이 된다는 말을 앞에서도 했다.
다른 장점도 있다.
- 매개변수 공유: 어떤 한 부분에서 이미지의 특성을 검출하는 필터가 이미지의 다른 부분에서도 똑같이 적용되거나 도움이 된다.
- 희소 연결: 하나의 출력값이 이미지의 일부(작은 입력값)에만 영향을 받고, 나머지 픽셀들의 영향을 받지 않기 때문에, 과대적합을 방지할 수 있다.
- 이동 불변성 보장: 이미지가 조금 바뀌어도 분석 매커니즘이 동일하기 때문에 동일하게 포착할 수 있다.
합성곱 신경망에서도 앞선 신경망들과 동일하게 손실함수의 합을 training set의 개수인 m으로 나누어 비용함수를 구할 수 있다. 그리고 경사하강법으로 비용함수를 최소화한다.
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기