컴퓨터 비전
이미지를 인식해서 구별하는 과정은 전에도 많이 이야기해왔다. 특히 최근에는 (피카소와 같이 특이한) 예술작품을 분석해서 비슷한 기법을 사용한 것처럼 사진을 변형하는 프로그램도 많다.
컴퓨터 비전에서의 사진은 보통 64 x 64 와 같이 픽셀의 개수 곱으로 나타낸다. 여기에 사진이 흑백이 아니라면 RGB 3개의 채널까지 곱해져 입체적인 행렬로 표현된다.
사진이 고화질(1000 x 1000 x 3)인 경우, 신경망을 통해 학습할 때 어려움을 겪을 수 있다. 너무 많은 변수(3,000,000)가 입력값이 되기 때문에 과적합 방지와 메모리를 통한 연산에 제약사항이 생긴다. 이를 해결하는 방법으로는 합성곱이 있다.
합성곱
합성곱(Convolution)은 일종의 필터링 과정이라고 볼 수 있다. 다음과 같이 수행한다.
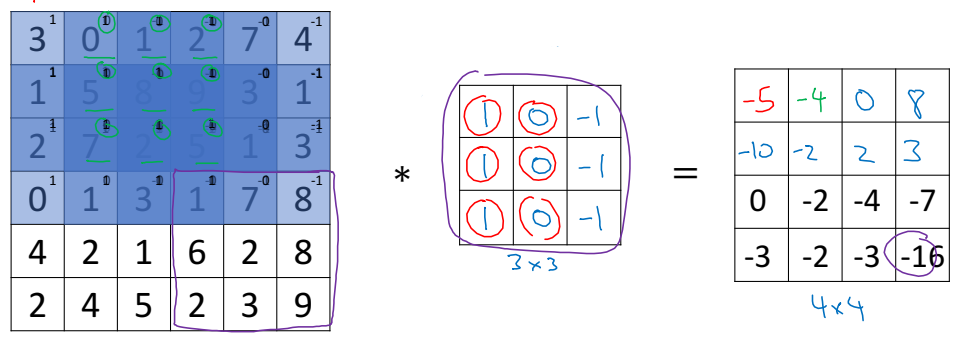
왼쪽의 행렬(6 x 6)을 오른쪽의 필터(혹은 커널)(3 x 3)를 이용해 필터링을 하는 과정이라고 보면 된다. 먼저, 필터를 가장 왼쪽 위에 올려두고, 겹쳐지는 요소들끼리 곱해서 이를 모두 더한다.
$3 \times 1 + 1 \times 1 + 2 \times 1 + 0 \times 0 + 5 \times 0 + 7 \times 0 + 1 \times (-1) + 8 \times (-1) + 2 \times (-1) = -5$
이 값이 결과의 가장 왼쪽 위의 요소가 된다.
다음은 필터를 오른쪽으로 한 칸 옮긴다. 그리고 앞선 과정과 동일하게 계산한다.
$0 \times 1 + 5 \times 1 + 7 \times 1 + 1 \times 0 + 8 \times 0 + 2 \times 0 + 2 \times (-1) + 9 \times (-1) + 5 \times (-1) = -4$
이제 이 과정을 계속 반복하면 결과 행렬을 얻을 수 있다.
cf. 사실 위 과정은 수학적으로는 합성곱이 아닌 ‘교차상관(Cross-correlation)’에 해당한다. 합성곱은 필터를 미러링하는 과정이 추가된다. 그러나 딥러닝에서는 관습적으로 위 과정을 합성곱이라고 부르며, 결과 값에 큰 영향을 주지 않기 때문에 별 문제가 없다.
합성곱으로 모서리 판별하기
이미지를 판별하는 데 가장 기본적인 단계는 모서리(edge)를 구분하는 것이다. 그 중에서도 기본적으로는 가로 모서리와 세로 모서리를 판독하는 것이다.
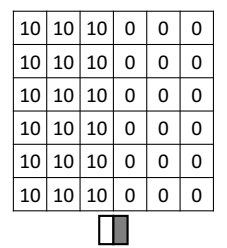
위와 같은 이미지가 있다고 하자. 왼쪽은 픽셀 값이 양수이니 밝은 색, 오른쪽은 0이니 어두운 색일 것이다. 이를 판별하는 필터는 다음과 같다.
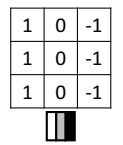
합성곱 계산 과정과 결과를 살펴보자.
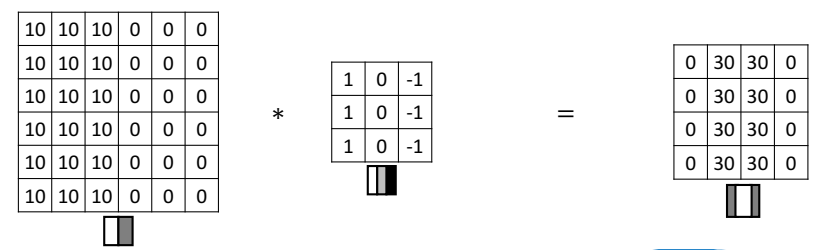
결과 이미지(4 x 4)를 보면, 가운데에 선명한 경계가 형성된 것을 볼 수 있다. 이를 통해 기존 이미지에 세로 모서리가 있었다는 사실을 파악할 수 있는 것이다.
반대로 가로 모서리를 파악하려면 어떻게 해야할까? 필터를 90도 회전하기만 하면 된다.
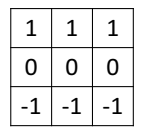
합성곱 결과는 다음과 같다.
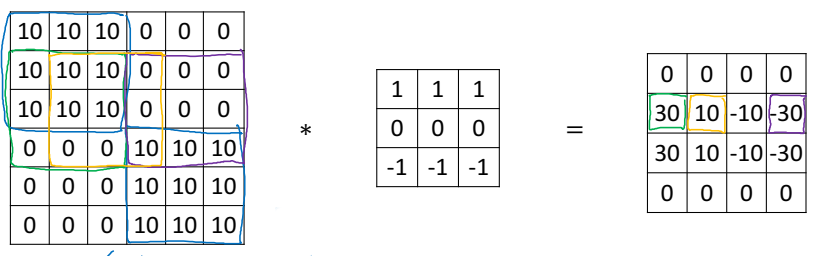
가로에 선명한 경계가 형성되는 것을 볼 수 있다. 물론 숫자가 조금씩 차이나기는 하지만, 실제로 더 사이즈가 큰 이미지를 다루게 되면 사소한 차이일 뿐이다.
모서리 판별에 사용하는 필터의 숫자들은 어떻게 결정된 것일까? 많은 연구가 있어왔고, 다양한 필터들이 있다.

왼쪽의 Sobel 필터는 가운데 숫자가 1이 아니라 2이다. 중간 부분 픽셀에 더 중점을 두고 합성곱을 하여, 경계가 더 선명하게 나타난다는 장점이 있다.
그러나 이제는 위와 같은 소모적인 연구와 논쟁이 필요가 없다. 우리는 딥러닝이라는 강력한 무기가 있다. 필터에 들어가는 숫자마저 학습을 통해 얻어낼 수 있다. 숫자들을 아래와 같이 미지수로 두고 역전파를 통해 최적의 필터를 찾아낼 수 있다.
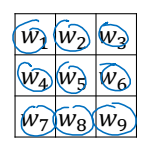
패딩
기존 합성곱 과정을 일반화해보자. (n x n)의 이미지를 (f x f)의 필터로 합성곱하면 결과는 (n - f + 1 x n - f + 1)의 이미지가 되었다.
\[(n \times n) * (f \times f) \rightarrow (n-f+1) \times (n-f+1)\]이 방법의 문제점은 크게 두 가지이다.
- 이미지가 축소된다.
- 가장자리의 픽셀은 계산에 한 번만 사용된다. 즉, 중요성이 떨어진다.
이를 해결하는 방법으로 ‘패딩(Padding)’이 있다. 겨울철에 패딩을 입는 것처럼 테두리에 픽셀을 덧대어주는 것이다. 이 방법으로 새로운 가장자리를 만듦으로써 기존 이미지의 픽셀들이 소외받지 않도록 만들 수 있다. 참고로 보통 가장자리에는 0을 둘러준다.
패딩을 고려하여 합성곱 결과를 일반화하면 다음과 같다. p는 몇 겹을 더했는지를 의미한다. \((n+2p-f+1) \times (n+2p-f+1)\)
패딩을 사용하는지의 여부에 따라 합성곱이 두 가지로 구분된다.
먼저, 유효(valid) 합성곱은 패딩(p)이 0일 때를 말한다. 이 경우에는 이미지 크기가 줄어드는 것을 피할 수 없다.
다음으로는 동일(same) 합성곱이 있다. 이는 합성곱의 결과 이미지가 기존 이미지와 동일하도록 하는 것이다. 즉,
$n+2p-f+1=n$
$p=\frac{f-1}{2}$
처럼 p를 설정하면 된다. 공식에서 볼 수 있듯이 f가 홀수여야 p를 정수로 만들 수 있다. 실제로도 필터는 홀수를 많이 사용한다.
스트라이드
스트라이드(Stride)는 ‘걸음’이라는 뜻을 가지고 있다. 합성곱에서 스트라이드는 ‘필터를 한 번에 얼마나 옮길 것인가’를 의미한다. 우리가 지금까지 했던 합성곱들은 스트라이드가 1인 합성곱이었던 것이다.
스트라이드(s)까지 반영하여 합성곱 결과를 일반화하면 다음과 같다.
\[\lfloor \frac{n+2p-f}{s} + 1 \rfloor \times \lfloor \frac{n+2p-f}{s} + 1 \rfloor\]정수가 나오지 않으면 내림한다.
입체 합성곱
지금까지 2차원 이미지, 즉 흑백 이미지의 합성곱들을 살펴보았다. 그럼 컬러 이미지의 합성곱은 어떨까?
입체 합성곱에서 컬러 이미지는 나머지는 흑백 이미지와 동일하지만 채널의 개수(이미지에서는 RGB)가 추가된다는 것만 다르다. 따라서 필터는 이미지와 채널의 개수를 맞추어주기만 하면 흑백에서와 똑같이 합성곱을 할 수 있다. 그림으로 이해해보자.
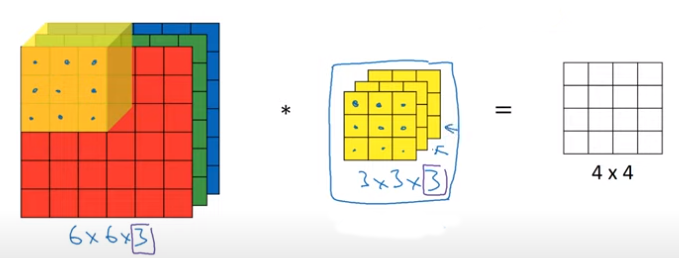
컬러 이미지에 필터 상자를 끼운 뒤, 필터를 이동시키면서 합성곱을 진행하면 된다. 놀랍게도 결과는 2차원이 된다.
필터에서 각각의 채널은 컬러 이미지에서의 R, G, B 패턴 분석을 담당한다. R의 패턴을 보고 싶다면 나머지 채널은 모두 0으로 만든 뒤 R채널만 원하는 숫자로 만들어주면 된다. 즉, 색상별로 나누어서 분석이 가능하다.
다양한 패턴을 분석하는 것 또한 가능하다. 가로 모서리와 세로 모서리를 동시에 보고 싶다면 각각 계산한 뒤 결과 이미지를 겹쳐 2개의 채널을 가지도록 하면 된다. 일반화를 하면 다음과 같다.
\[(n \times n \times n_c) * (f \times f \times n_c) \rightarrow (n-f+1) \times (n-f+1) \times n_c'\]$n_c$는 채널의 개수, $n_c’$ 분석하고자 하는 패턴의 개수이다.
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기