초매개변수 선택하기
지금까지 살펴본 초매개변수에는 여러 가지가 있었다. 학습률 $\alpha$, 모멘텀 $\beta$, 신경망 층의 수, 은닉 유닛의 개수 등.
초매개변수라고 다 같은 중요도를 가지는 것은 아니다. 중요도 순서에 따라 초매개변수의 티어(?)를 분류해보면 다음과 같다.
| 우선순위 | 초매개변수 |
|---|---|
| 티어 1 | $\alpha$(학습률) |
| 티어 2 | $\beta$(모멘텀), 은닉유닛의 개수, 미니 배치의 크기 |
| 티어 3 | 신경망 층의 개수, 학습률 감쇠 속도 |
| 티어 4 | $\beta_1$, $\beta_2$, $\epsilon$(Adam 최적화 알고리즘) |
초매개변수를 선택하는 방법에는 크게 3가지 정도가 있다.
첫 번째 방법은 초매개변수의 수가 적었던 과거에 주로 사용했던 방법이다. 격자점을 이용하는 것으로, 좌표평면처럼 두 매개변수를 각각 축으로 놓고 매개변수의 조합을 선택하는 것이다. 그러나 이 방법은 절대로 추천하지 않는다. 앞서 티어를 왜 정했겠는가? 모든 초매개변수를 동등하게 대할 수는 없는 법이다. 격자법을 사용하게 되면 초매개변수의 중요도에 관계없이 모두 동등한 가짓수를 고려하게 된다. 더 중요한 초매개변수에 대해 집중적으로 많은 경우를 생각해볼 수 없다는 뜻이다.
두 번째 방법으로는 무작위적으로 매개변수를 선택하는 것이다. 가장 즐겨 사용되는 방법으로써, 매우 많은 초매개변수를 고려해야 하는 현재 머신러닝에도 적합하다. 더 중요한 초매개변수의 경우 더 많은 경우를 시도해볼 수도 있다.
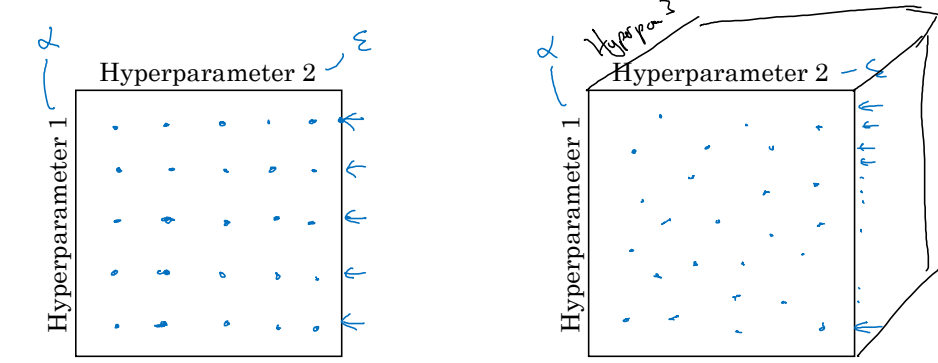
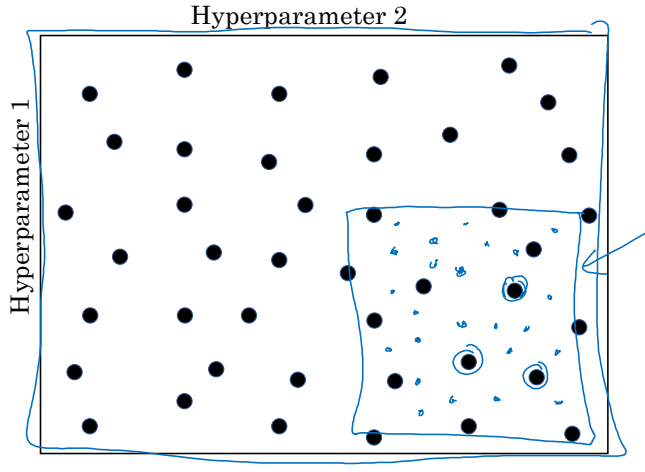
마지막 방법은 '정밀화 접근'으로 불린다. 두 번째 방법과 비슷하게 무작위를 사용하긴 하지만, 조금 더 선택과 집중을 한다. 좋은 성능을 보이는 초매개변수의 조합이 발견되면, 그 지역을 줌인(Zoom-In)해서 주변을 더 집중적으로 탐색하는 방법이다.
무작위 초매개변수 선택에서 스케일 조정하기
초매개변수 선택에서 스케일을 조정하는 것은 중요하다. 스케일을 제대로 조정하지 않으면 결과가 완전히 달라질 수 있기 때문이다.
먼저, 스케일 조정이 필요 없는 경우를 보자. 은닉 유닛의 개수나 은닉 층의 개수는 특정한 정수, 즉 불연속적인 분포를 가지며 고르게 분포(uniformly distributed) 되어 있다. 이런 경우는 그냥 무작위적으로 조합을 선택해도 상관이 없다.
하지만, 학습률을 0.0001과 1 사이에서 선택하는 경우를 생각해보자. 만약 이 상황에서 그냥 선형적인 무작위 선택을 하게 되면 0.0001과 0.1 사이에서 전체 탐색의 90%에 달하는 값이 나오게 된다. 이럴 경우 모든 구간을 균일하게 탐색했다고 말하기 어려울 것이다.
좋은 해결책은 로그($log$) 스케일을 사용하는 것이다. 0.0001에 로그를 취하면 $\log{10^{-4}}=-4$이고, 1에 로그를 취하면 $\log{10^0}=0$이다. 그럼 우리는 -4와 0 사이를 선형적으로 무작위 탐색한 뒤 그 값을 10의 지수로만 취해주면 학습률을 구할 수 있는 것이다. 이렇게 하면 모든 구간을 동등하게 탐색했다고 말할 수 있다.
모멘텀 초매개변수 $\beta$를 선택할 때도 마찬가지다. $\beta$가 0.9와 0.999 사이라고 할 때, 이 구간에서 그냥 선형적인 무작위 탐색을 하는 것은 좋지 않다. 특히, $\beta$의 경우 1에 가까워지면 질수록 작은 차이도 결과에 매우 큰 영향을 끼치게 된다(평균에 반영하는 구간의 길이가 달라지기 때문). 이럴 때는 1에서 $\beta$를 빼서 0.1와 0.001의 구간으로 만든 뒤, 학습률과 마찬가지로 로그 스케일로 탐색하는 것이 좋다.
실전에서 초매개변수 다루기
아무리 한 번 제대로 된 초매개변수를 선택했다고 해도, 데이터가 조금 변화하거나 모델을 개선하면 전혀 엉뚱한 결과가 도출될 수 있다. 초매개변수는 지속적으로 적절 여부를 확인하며 업데이트하는 것이 좋다.
초매개변수를 다루는 것(tuning)에는 두 가지 방법이 있다.
첫 번째 방법은 한 번에 하나의 모델 다루기(Babysitting one model)이다. CPU와 GPU 성능이 제한적이라 한 번에 많은 모델을 테스트하기 어려울 때 사용한다. 모델을 매일 보면서 성능이 개선되는지를 확인하고, 초매개변수를 바꾸는 방법이다. 초매개변수를 바꾸고 나서는 성능이 증가할 수도 있고, 하락할 수도 있다. 극적인 효과를 기대하기 보다는 매일 조금씩 개선해나아가는 것이다. 마치 판다가 아기를 키우는 것과 같다고 하여 판다 접근로 부르기도 한다.
다른 방법은 동시에 많은 모델 다루기(Training many models in parallel)이다. 컴퓨터 성능이 좋아 한 번에 많은 모델을 다룰 수 있을 때 사용한다. 각기 다른 초매개변수를 적용한 다양한 모델을 돌리고 가장 뛰어난 성능을 보이는 모델을 선택하면 되는 것이다. 생선이 매우 많은 알을 낳아놓는 것과 같다고 하여 캐비어 접근이라고도 한다.

모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기