미니 배치(Mini-batch) 경사하강법
m개의 매우 많은 데이터가 있다고 해보자. 한 번 경사하강법을 진행할 때마다 이 데이터를 모두 거쳐서 계산하려면 매우 시간이 오래 걸릴 것이다.
이를 해결하기 위해 미니 배치(Mini-batch) 경사하강법이 개발되었다. 이 기법은 매우 많은 데이터를 일정한 묶음으로 만든 뒤, 각각의 묶음에 대해서 1회씩만 경사하강법을 진행하는 것이다.
예를 들어 5,000,000개의 데이터가 있다고 해보자. 먼저, 이를 1,000개씩 묶어서 5,000개의 묶음을 만든다. 그리고 각각의 묶음에 대해서 1회만 경사하강법을 실시, 총 5,000번의 경사하강법을 실시해서 모델을 학습시킨다. 이를 코드로 구현하면 다음과 같다.
for t = 1, ..., 5000 {
Forward prop on X{t}
Z[1] = W[1]X{t} + b[1]
A[1] = g[1](Z[1])
...
A[L] = g[L](Z[L])
Compute cost J{t}
Backprop to compute gradients cost J{t}(using (X{t}, Y{t}))
W[l] = W[l] - learning_rate * dW[l]
b[l] = b[l] - learning_rate * db[l]
}
미니 배치 경사하강법에서 윗 첨자 ‘{t}’는 몇 번째 묶음인지를 나타낸다. 데이터 전체를 한 번 훑는 과정을 ‘1 epoch’라고 한다.
미니 배치 경사하강법과 비용함수
일반적인(배치) 경사하강법은 반복횟수가 많을수록 다음과 같은 비용함수 그래프를 가진다.
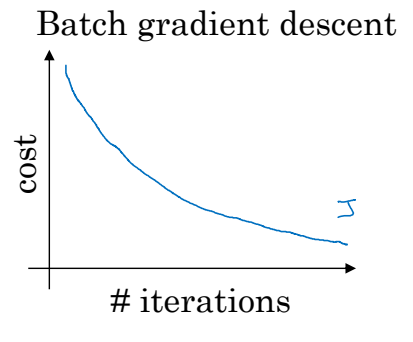
비용함수는 무조건 계속 감소해야하며, 만약 조금이라도 증가했다면 잘못된 과정이 끼어있다.
하지만 미니 배치 경사하강법에서는 경사하강법을 시도한 묶음의 수가 증가한다고 해서 비용함수가 꼭 감소하지만은 않는다.
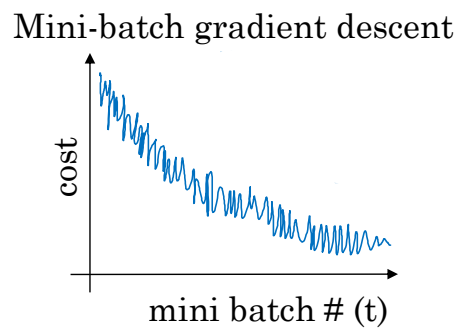
전체적으로는 감소하는 형태이지만 노이즈가 발생한다.
미니 배치 사이즈 설정하기
그렇다면 미니 배치의 사이즈(한 묶음에 들어가는 데이터의 개수)는 어떻게 설정해야할까?
만약 미니 배치의 사이즈가 전체 데이터의 개수 m이라고 해보자. 이런 상황에서는 일반적인 배치 경사하강법과 다를 바가 없을 것이다. 경사하강법이 최적의 경로를 통해 가장 효율적으로 진행될 것이지만(파란색 선), 한 반복당 시간이 너무 오래 걸릴 것이다.
그럼 미니 배치의 사이즈가 1이라고 해보자. 이런 상황을 확률 경사하강법(Stochastic gradient descent)이라고 한다. 한 반복당 소요되는 시간은 매우 적겠지만, 경사하강법이 최적으로 적용될 수도 없고(보라색 선), 벡터화를 통한 이점도 얻을 수 없는 방법이다.
우리가 원하는 사이즈는 그 중간 어딘가의 사이즈이다. 벡터화를 통한 이점도 얻으면서 한 반복당 시간도 그렇게 오래걸리지 않는 그 지점말이다. 또한, 경사하강법도 어느 정도 잘 적용되어야 한다(초록색 선).
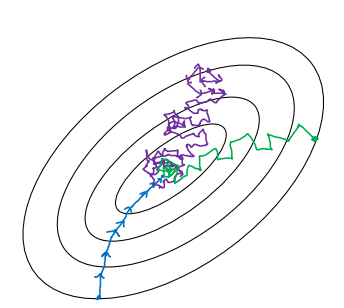
그러나 애석하게도, 가장 좋은 사이즈를 정확하게 알 수 있는 방법이 없다.
만약 training set의 사이즈가 작다면, 그 자체로 그냥 배치 경사하강법을 적용하는 것이 좋을 것이다.
미니 배치 경사하강법을 사용하고 싶다면 보통 2의 제곱으로 사이즈를 결정한다. 이는 컴퓨터 메모리의 작동방식을 고려한 것으로, $2^6$, $2^7$, $2^8$이 가장 선호되는 숫자들이다.
마지막으로, CPU와 GPU의 메모리에 미니 배치가 적절한지를 고려해야한다. 만약 그렇지 않다면, 성능이 떨어질 수도 있다.
미니 배치 사이즈는 또다른 초매개변수이다. 그 말인 즉슨, 여러 값을 시도하면서 가장 적절한 것을 찾아야 한다는 의미이다.
지수 가중 평균
런던의 기온 데이터를 가지고 일정 구간의 평균이나 이동 흐름의 평균을 구하고 싶다고 가정해보자. 이 과정에는 다음과 같은 공식을 사용할 수 있다.
$v_0 = 0$
$v_1 = 0.9v_0 + 0.1\theta_1$
$v_2 = 0.9v_1 + 0.1\theta_2$
$\cdots$
$v_t = 0.9v_{t-1} + 0.1\theta_t$
이 과정을 통해 구해진 값들을 나타내면 다음 그림의 빨간색 선과 같아진다.
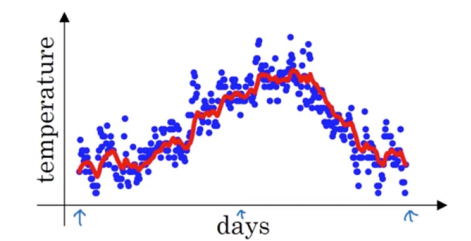
이와 같이 데이터의 평균 흐름을 계산하고자 할 때 지수 가중 평균을 이용할 수 있다. 보편적인 공식은 다음과 같다.
\[v_t = \beta v_{t-1} + (1-\beta)\theta_t\]여기서는 $\beta$ 값이 중요하다. $\beta$에 따라 평균에 반영하게 될 구간이 달라지기 때문이다. 만약 $\beta$가 0.9라면, 과거 약 10일의 기온을 평균에 반영하겠다는 의미이고, $\beta$가 0.98이라면, 과거 약 50일의 기온을 평균에 반영하겠다는 뜻이 된다. (계산은 약 $\frac{1}{1-\beta}$로 할 수 있다.)
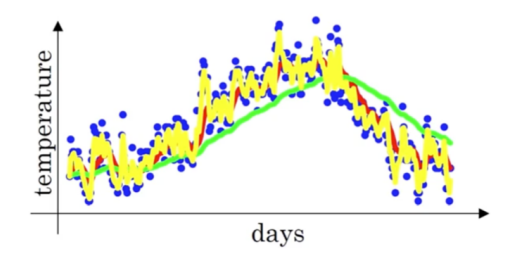
$\beta$에 따른 지수 가중 평균의 그래프이다. $\beta$가 클수록 평균 계산에 더 많은 날을 반영하기 때문에 곡선이 더 부드러워지지만, 범위가 커지므로 개별 데이터에서는 멀어지는 것을 관찰할 수 있다.
지수 가중 평균 깊이있게 이해하기
지수 가중 평균의 공식을 조금 더 깊이있게 파헤쳐보자.
t가 큰 순서부터 공식을 다시 작성할 수 있다.
$v_{100} = 0.9 v_{99} + 0.1 \theta_{100}$
$v_{99} = 0.9 v_{98} + 0.1 \theta_{99}$
$v_{98} = 0.9 v_{97} + 0.1 \theta_{98}$
$\dots$
첫 번째 공식을 풀어서 써보자.
$v_{100} = 0.1 \theta_{100} + 0.9 v_{99}$
$= 0.1 \theta_{100} + 0.9 (0.1 \theta_{99} + 0.9 v_{98})$
$= 0.1 \theta_{100} + 0.9 (0.1 \theta_{99} + 0.9 (0.1 \theta_{98} + 0.9 v_{97}))$
$= 0.1 \theta_{100} + 0.1 \cdot 0.9 \theta_{99} + 0.1(0.9)^2 \theta_{98} + 0.1(0.9)^3 \theta_{97} + \cdots$
마치 다음 두 그래프를 elementwise한 결과가 도출된다.
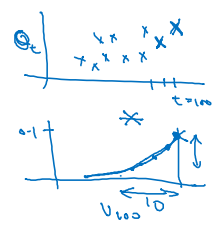
지수적으로 감소하는 형태의 그래프가 나타날 것이다.
얼마의 기간이 이동하면서 평균이 구해졌는가는 다음처럼 구할 수 있다. $\beta = 1-\epsilon$ 이라고 하면 $(1-\epsilon)^n = \frac{1}{e}$ 을 만족하는 n이 그 기간이 된다. 보통 n은 $\frac{1}{\epsilon}$이다.
지수 가중 평균을 이용해서 평균을 구하는 과정은 다음과 같은 코드로 나타낼 수 있다.
v_theta = 0
Repeat {
Get next theta_t
v_theta = beta * v_theta + (1 - beta) * theta_t
}
위 과정을 보면 알겠지만 계속해서 $v_{\theta}$를 덮어쓰면서 메모리를 아끼는 것을 확인할 수 있다. 이처럼 지수 가중 평균은 직접 평균을 구하는 과정보다는 부정확하지만 비용 측면에서 이점이 있다.
지수 가중 평균에서의 편향 수정
지수 가중 평균을 구할 때 초반 과정을 다시 떠올려보자.
$\beta = 0.98$
$v_{0} = 0$
$v_{1} = 0 + 0.02 \theta_{1}$
$v_{2} = 0.98 \times 0.02 \times \theta_{1} + 0.02 \theta_{2}$
초반 값, 특히 $v_{1}$, $v_{2}$ 들이 실제 값 $\theta_{1}$, $\theta_{2}$에 비해 현저히 작게 추정되는 것을 확인할 수 있다. 보통 개발자들은 지수 가중 평균을 시작하고 좀 시간이 지난 후의 값을 이용하여 편향을 무시하게 되지만, 초반에 발생하는 이러한 불편한 상황을 못 견디는 사람이 있을 수도 있다.
이럴 때는 편향을 수정해주면 된다. 그냥 $v_{t}$ 대신 $\frac{v_{t}}{1-\beta^t}$를 사용하게 하는 것이다. 그럼 아래 그림의 초록색 선처럼 초반의 편향을 방지할 수 있다.
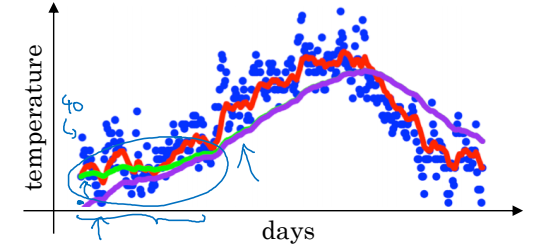
모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기