입력 정규화하기
입력은 항상 같은 스케일을 가지지 않는다. 예를 들어 어떤 특성은 0~5의 범위를 가질 수도 있고, 다른 특성은 0~3까지의 특성을 가질 수도 있다.
이를 정규화하기 위한 방법에는 크게 두 가지가 있다.
첫 번째로는 평균으로 빼는 방법이다. 각 특성마다 평균을 구해서 이를 값에서 빼주면 어느 정도 정규화를 할 수 있다. 편차를 구하는 것이다.
두 번째로는 분산을 1로 만드는 것이다.
\[\sigma^2 = \frac{1}{m} \displaystyle \sum_{i=1}^{m}{x^{(i)2}}\] \[x /= \sigma^2\]위와 같은 과정을 통해 분산을 1로 만들 수 있다.
입력을 정규화하는 과정은 train set 뿐만 아니라 test set에서도 진행해주는 것이 좋다.
그렇다면 왜 정규화를 해야할까?
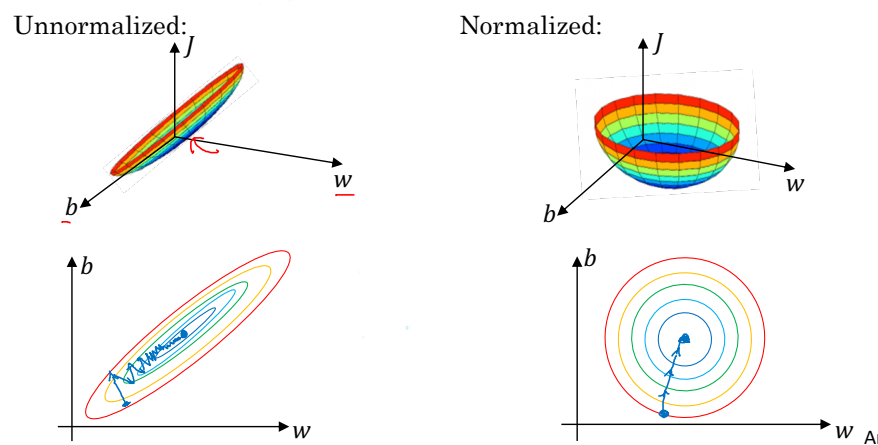
왼쪽은 정규화를 하지 않은 상태이고, 오른쪽은 정규화가 진행된 상태이다. 보이다시피 정규화를 진행하면 대칭형태를 띠는 반면, 정규화를 진행하지 않으면 동고선의 형태를 띤다. 대칭적인 모양을 가지는 경우 경사하강법을 적용할 때 더 높은 학습률로 빠르게 진행할 수 있다. 따라서 대칭적인 모양을 가지도록 정규화를 진행해야 한다.
가중치 W의 초기화
활성함수와 상수가 다음과 같이 주어졌을 때 y값을 구해보자.
\[g(z)=z \quad b^{[l]} = 0\] \[\hat{y} = W^{[L]}W^{[L-1]} \cdots W^{[2]}W^{[1]}x\]W를 계속해서 곱해나가는 상황인 것을 알 수 있다. 그런데, W를 매우 많이 곱하는 깊은 신경망에서 W가 I(단위행렬)가 아닌 경우에는 어떨까? 다음과 같은 두 가지 상황이 발생할 수 있을 것이다.
- $W^{[l]} > I$: y가 기하급수적으로 증가
- $W^{[l]} < I$: y가 기하급수적으로 감소
둘 다 좋지 않은 상황이다. 이를 위해서는 W를 적절히 초기화해주는 것이 중요하다.
$z=w_{1}x_{1}+w_{2}x_{2}+\cdots+w_{n}x_{n}$이므로, n이 많으면 w를 줄이는 것이 좋다. 이를 위해 보통의 경우 w의 분산을 $\frac{1}{n}$ (n은 이전 신경망 node의 개수) 으로 설정한다. 의사코드로 쓰면 다음과 같다.
W[l] = np.random.randn(shape) * np.sqrt(1/n[l-1])
코드의 마지막 부분에 주목하자.
설정해주는 w의 분산이 항상 $\frac{1}{n}$인 것은 아니다. ReLU 함수를 사용하는 경우에는 $w_i$의 분산을 $\frac{2}{n^{[l-1]}}$, tanh 함수인 경우에는 $\frac{1}{n^{[l-1]}}$ 또는 $\frac{2}{n^{[l-1]} + n^{[l]}}$로 한다.
기울기의 수치 근사
앞서 기울기를 구할 때 매우 작은 수인 $\epsilon$을 더한 것이 기억날 것이다. 여기서는 $\epsilon$을 더하는 것 뿐만 아니라 빼서도 구한다.
$f(\theta)=\theta^3$라 하자.
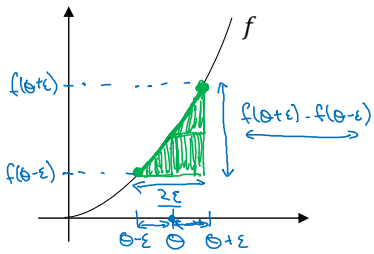
실제 값을 이용해서 단지 $\epsilon$을 더하기만 했을 때와 비교해보라. 확실히 더 나은 근사 값이 구해질 것이다. 앞으로 기울기를 구할 때는 이처럼 아주 작은 값을 더하고 빼는 것 모두를 활용할 것이다.
경사 검사
역방향전파에서 경사하강법이 제대로 진행되었는지를 확인하는 방법도 알아두어야겠다. 이를 위해서는 사전 준비가 조금 필요하다. 먼저, $W^{[1]}, b^{[1]}, …, W^{[L]}, b^{[L]}$을 큰 벡터 $\theta$로 연결(concatenate)해야 한다. 비용함수 $J(W, b)$ 를 $J(\theta)$로 바꾸는 과정이라고 생각하면 된다. 마찬가지로 $dW^{[1]}, db^{[1]}, …, dW^{[L]}, db^{[L]}$ 역시 큰 벡터 $d\theta$로 연결한다.
다음으로는 각각의 i에 대하여 기울기 근사 값을 구해주는 것이다. 과정은 다음과 같다.
\[d\theta_{approx}^{[i]} = \frac{J(\theta_1, \theta_2, \dots, \theta_i + \epsilon, \dots) - J(\theta_1, \theta_2, \dots, \theta_i - \epsilon, \dots)}{2\epsilon} \\ \approx d\theta^{[i]} = \frac{\partial J}{\partial \theta_{i}}\]이 과정으로 구한 $d\theta_{approx}^{[i]}$는 다음과 같은 정규화 과정을 거친다.
\[\frac{\lVert d\theta_{approx} - d\theta \rVert_2}{\lVert d\theta_{approx} \rVert_2 + \lVert d\theta \rVert_2}\]이 값이 우리가 설정한 $\epsilon$ 보다 작거나 비슷하다면 경사하강법이 알맞게 적용된 것이다. 그러나, 터무니 없이 큰 값이 나왔다면 다시 검증해봐야 한다. 참고로, 보통 $\epsilon = 10^{-7}$의 값을 설정한다.
경사 검사에서는 다음과 같은 사항을 주의해야한다.
- 기울기의 근사값을 구하는 과정은 매우 느린 과정이다. 따라서 훈련 때는 경사 검사를 실시하지 않고 오직 debug에서만 한다.
- 경사 검사를 통과하지 못했다면 각각의 요소들을 분석해서 버그를 찾아낸다.
- 정규화 공식을 기억해라. 단지 손실함수를 m으로 나누는 것이 아니라 공식 뒤에 뭐가 더 붙어있었다.
- Dropout 기법에서는 사용하지 않는다.
- 가끔 무작위 초기화를 해도 초기에 경사 검사가 잘 되는 경우가 있다. 이때는 훈련을 조금 시킨 다음에 경사 검사를 다시 해본다.
모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기