로지스틱 회귀에서의 정규화
로지스틱 회귀에서의 비용함수는 다음과 같이 정의되었다.
\[\displaystyle J(w, b) = \frac{1}{m} \sum_{i=1}^{m}{L(\hat{y}^{(i)}, y^{(i)})}\]정규화를 위해서는 이 뒤에 정규화 매개변수 $\lambda$를 포함하는 식을 추가해준다.
\[\displaystyle J(w, b) = \frac{1}{m} \sum_{i=1}^{m}{L(\hat{y}^{(i)}, y^{(i)})} + \frac{\lambda}{2m}{\lVert w \rVert}_{2}^{2}\]위 식은 $L_{2}$ 정규화이다. ${\lVert w \rVert}_{2}^{2}$ 는 다음과 같이 구한다.
\[{\lVert w \rVert}_{2}^{2} = \sum_{j=1}^{n_x}{w_j^2} = w^{T}w\]$L_{1}$ 정규화도 있다. 다음처럼 구한다.
\[\sum_{j=1}^{n_x}{|w_j|}\]실제로는 $L_{2}$ 정규화를 더 많이 사용한다. 또한, w가 아닌 b는 빠뜨려도 괜찮은데, 거의 모든 매개변수가 w에 존재하기 때문이다.
정규화를 진행하면 w 내부에 0이 많아진다.
신경망에서의 정규화
이제 신경망에서의 정규화를 살펴보자.
\[\displaystyle J(w^{[1]}, b^{[1]}, ..., w^{[L]}, b^{[L]}) = \frac{1}{m} \sum_{i=1}^{m}{L(\hat{y}^{(i)}, y^{(i)})} + \frac{\lambda}{2m}\sum_{l=1}^{L}{\lVert w^{[l]} \rVert_{F}^{2}}\]식은 매우 유사하다. 다만, $\lVert w^{[l]} \rVert_{F}^{2}$ 가 마음에 걸릴 수 있는데, 다음과 같이 계산한다.
\[\lVert w^{[l]} \rVert_{F}^{2} = \sum_{i=1}^{n^{[l]}}\sum_{i=1}^{n^{[l-1]}}{(w_{ij}^{[l]})^2}\]이를 Frobennius norm이라고 부른다.
경사하강법을 구현해보자. 계산과정을 살펴보면 될 듯하다.
\[dW^{l} = (from\,backprop) + \frac{\lambda}{m}W^{[l]}\]위 식을 대입해보면
\[W^{[l]} = W^{[l]} - \alpha W^{[l]}\] \[W^{[l]} = W^{[l]} - \alpha[(from\,backprop) + \frac{\lambda}{m}W^{[l]}]\\ = W^{[l]} - \frac{\alpha\lambda}{m}W^{[l]} - \alpha(from\,backprop)\\ = (1-\frac{\alpha\lambda}{m})W^{[l]} - \alpha(from\,backprop)\]이렇게 된다.
마지막줄에서 $W^{[l]}$ 의 계수를 주목해보자. 1보다 작다. 이는 가중치(w)가 점점 감소한다는 의미이다.
정규화의 효과
왜 정규화가 효과가 있을까? 아래 식을 다시 보자.
\[\displaystyle J(w^{[l]}, b^{[l]}) = \frac{1}{m} \sum_{i=1}^{m}{L(\hat{y}^{(i)}, y^{(i)})} + \frac{\lambda}{2m}\sum_{l=1}^{L}{\lVert w^{[l]} \rVert_{F}^{2}}\]여기서 $\lambda$ 를 크게 하면 (앞선 단락 마지막에 보았듯이) w를 0에 가깝도록 만들 수 있다. 이는 신경망에서 은닉층을 줄여 신경망의 형태를 로지스틱 회귀에 가깝도록 할 수 있다는 뜻이다. 은닉층에 존재하는 node들의 영향력을 감소시키는 것이다.
$g(z)=\tanh{(z)}$ 라 하자. w의 값이 작아지면 $z^{[l]} = W^{[l]}a^{[l-1]} + b$ 에 의해 z가 작아지게 되고, 이는 활성화함수의 구간을 좁히는 역할을 한다. tanh의 경우 원점 주위에서 거의 1차에 가까운 직선 형태를 가지고 있으므로, 원점 주위에서는 매우 간단한 함수라고 생각할 수 있다. 즉, 과대적합을 방지할 수 있는 것이다.
정리하자면, $\lambda$ 의 증가로 $W^{[l]}$ 이 감소하고, 따라서 z가 감소해서 신경망이 로지스틱 회귀에 가깝게 된다. 그리고 복잡한 함수에서 변형된 간단한 함수는 과적합을 방지할 수 있기에, 결국 정규화가 효과를 발휘하게 된다.
추가로, 우리는 경사하강법을 반복할수록 비용함수가 감소하기를 바란다. 그러나 이전의 비용함수 식만을 사용하면 단조감소를 관찰하기가 불가능하다. 이번에 새롭게 정의한 정규화를 적용한다면 비로소 단조감소하는 비용함수를 관찰할 수 있을 것이다.

Dropout 정규화
Dropout 정규화의 아이디어는 간단하다. 은닉층에 존재하는 node를 일정 비율로 랜덤하게 제거하여 단순한 신경망을 만드는 것이다. 이때 각각의 은닉층에서 유지되는 node의 비율을 ‘keep-prob’라고 한다.
구현과정 역시 간단하다. 먼저, keep-prob를 설정한 뒤, 은닉층에 이를 적용하여 node를 랜덤하게 제거한다. 그리고 이전 신경층의 결과를 이용해 계산을 거쳐 다음 신경망 계산에 사용할 결과를 도출하면 되는 것이다.
주의할 것은, inverted dropout이라는 과정이 중간에 포함된다는 점이다. 이는 단순화된 은닉층으로 결과를 낸 직후에 그 결과를 keep-prob으로 나누는 것을 의미한다. 이는 다음 신경층에서 기댓값을 낮추지 않기 위한 조치이다.
테스트를 진행할 때는 keep-prob를 1로 두고 실시한다. 즉, dropout을 하지 않는다는 의미이다. 따라서 테스트 진행 시에는 굳이 inverted dropout을 할 필요가 없다.
Dropout 정규화가 작동하는 이유
그렇다면 왜 dropout 정규화가 작동할까?
직관적으로 이해해보자. Dropout 정규화는 랜덤하게 은닉층의 node를 삭제하여 입력을 불규칙하게 바꾼다. 랜덤하게 입력이 바뀌기 때문에 어떤 하나의 특성에 의존하지 못하도록 만든다는 것이다. 이를 해결하는 방법은 매개변수(w)를 적절히 분산시켜 특정한 특성에 대한 의존도를 낮추는 수밖에 없다. 그런데 w가 낮아지면 어떤 현상이 발생하는가? 앞서 정규화가 작동하는 원리에서 본 것과 동일한 상황이 되는 것이다!!!
은닉층에 따라 keep-prob를 다르게 설정해도 된다. 특히, node가 많은 층(매개변수가 많은 층)의 경우에는 강력한 keep-prob를 통해 과대적합을 방지하는 것이 도움이 된다.
Dropout 정규화에도 단점은 있다. 비용함수가 잘 정의되지 않기 때문에, 경사하강법을 시행할수록 비용함수가 단조감소하는 모습을 보기는 쉽지 않다. 만약 이를 확인하고 싶다면 dropout을 멈추고 디버깅을 하자.
다른 정규화 방법
다른 다양한 정규화 방법도 있다.
먼저, 데이터를 증가시키는 것이다. 많은 데이터를 수집하는 것도 있겠지만, 기존의 데이터를 조금씩 변형하는 것도 효과가 있을 수 있다. 예를 들어 사진을 좌우 대칭하거나 비틀어 왜곡하는 것이 있다. 데이터를 수집하는 것만큼 좋진 않지만, 그래도 어느 정도는 의미가 있다.
다른 방법으로는 조기종료(Early stopping)가 있다.
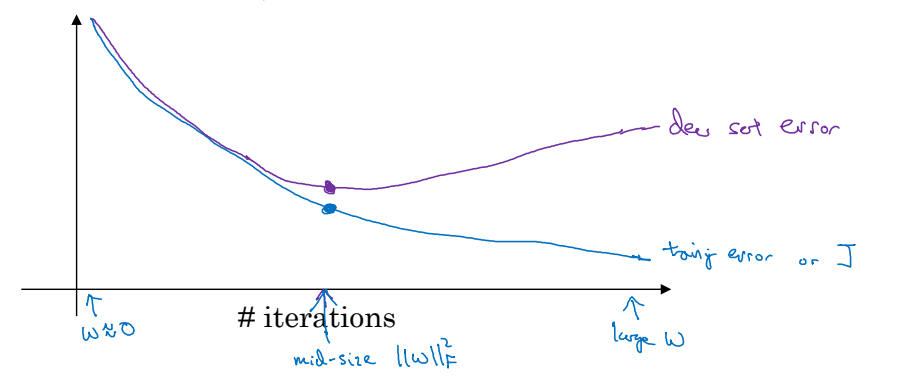
위 그래프를 보면, dev set의 경우 일정 반복 이상이 되면 비용함수가 오히려 증가하는 것을 확인할 수 있다. 해당 시점 이후부터는 모델이 train set에 과적합 되어있기 때문으로 볼 수 있다. 따라서 dev set의 비용함수가 증가하는 시점에서 훈련을 멈추면 과적합을 방지할 수 있다. 매개변수 w역시 너무 작지도, 너무 크지도 않은 적절한 값을 가지게 될 것이다.
조기종료는 매우 편리하지만 치명적인 문제점을 가지고 있기도 하다. 머신러닝 개발과정에서 우리는 두 가지에 관심을 가지고 있다. 비용함수를 최적화 하는 것과 과적합을 막는 것이다. 이 두 가지는 서로 분리해서 생각해야하는 문제이다. 그러나 조기종료는 이 두 가지를 섞어서 해결해버린다. 각각을 따로 해결할 수가 없는 것이다.
조기종료의 대안으로는 앞서 살펴본 다른 정규화를 이용하면 된다. 그러나 앞선 $L_{2}$정규화나 dropout 정규화 역시 적절한 매개변수 $\lambda$를 노가다로 찾아야 한다거나, 비용함수의 단조감소를 확인할 수 없는 등의 문제점을 가지고 있다.
모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기