심층 신경망
심층 신경망은 얕은 신경망에 비해 은닉층이 더 많은 신경망을 의미한다.
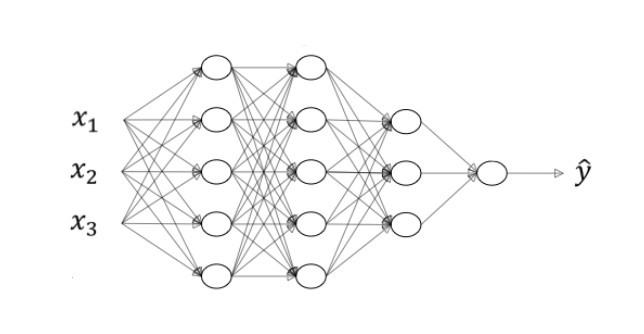
심층 신경망에서 사용되는 다양한 표기법에 대해 알아보자.
- L: 층의 개수 (ex. L = 4: 층이 4개)
- $n^{[l]}$: $l$번째 층에 속한 유닛의 개수 (ex. $n^{[1]} = 5$: 첫번째 층의 유닛이 5개)
- $a^{[l]}$: $l$번째 층의 활성화 값
심층 신경망에서의 정방향 전파
심층 신경망에서의 정방향 전파라고 해서 얕은 신경망과 크게 다르거나 하지 않다.

위 신경망에서 첫 번째 층의 정방향 전파 계산 과정은 다음과 같다.
\[z^{[1]} = W^{[1]}a^{[0]} + b^{[1]}\] \[a^{[1]} = g^{[1]}(z^{[1]})\]두 번째 은닉층의 계산 과정은 아래와 같다.
\[z^{[2]} = W^{[2]}a^{[1]} + b^{[2]}\] \[a^{[2]} = g^{[2]}(z^{[2]})\]두 과정이 매우 유사하게 생긴 것을 확인할 수 있을 것이다. 따라서 이를 일반화할 수 있으며, 반복문을 최대한 피하기 위해 벡터화도 적용할 것이다.
\[Z^{[l]} = W^{[l]}A^{[l - 1]} + b^{[l]}\] \[A^{[l]} = g^{[l]}(Z^{[l]})\]그리고 이 과정을 여러 개의 은닉층에서 반복해야 한다. 여기서는 아쉽게도 반복문을 피할 수 없다. 따라서 위의 공식을 신경층의 개수만큼 반복해주어야 한다.
행렬의 차원 확인하기
신경망을 코딩할 때 가장 버그가 많이 생기는 곳은 행렬의 차원에 관한 부분이다. 행렬의 차원을 잘못 지정하여 행렬 간 연산이 되지 않는다면 코드가 제대로 실행되지 않을 것이다.

일단 벡터화를 하지 않았다고 생각하고 행렬의 차원을 생각해보자. 첫 번째 은닉층에서의 첫 계산은 다음과 같다.
\[z^{[1]} = W^{[1]}x + b^{[1]}\]z는 (3, 1) 행렬, x는 (2, 1) 벡터이다. 이로부터 W가 (3, 2) 행렬이라는 것을 도출할 수 있다(행렬 간 곱셈이 가능해야하기 때문). b는 (3, 1) 행렬이 될 것이다. 조금 일반화하면 z는 $(n^{[l]}, 1)$, W는 $(n^{[l]}, n^{[0]})$, x는 $(n^{[0]}, 1)$, b는 $(n^{[1]}, 1)$ 이 될 것이다. 완전히 일반화하면 다음과 같다.
- $W^{[l]}:\,(n^{[l]}, n^{[l - 1]})$
- $b^{[l]}:\,(n^{[l]}, 1)$
- $dW^{[l]}:\,(n^{[l]}, n^{[l - 1]})$
- $db^{[l]}:\,(n^{[l]}, 1)$
dW와 db는 각각 W와 b의 차원과 동일하다.
그 다음 계산은 다음과 같다.
\[a^{[1]} = g^{[1]}(z^{[1]})\]여기서는 a와 z가 같은 차원을 가져야 한다는 것을 알 수 있다.
이번에는 벡터화한 경우를 살펴보자. 벡터화를 하면 벡터 x가 행렬 X가 되는 것이기 때문에 W의 차원은 변하지 않는다. 또한, b의 차원 역시 그대로 두어도 broadcasting에 의해 파이썬이 알아서 계산을 잘 수행한다.
변하는 것은 계산 결과에 해당한다고 할 수 있는 a와 z이다. 모두 벡터에서 행렬이 된다. 행렬 X가 $(n^{[l-1]}, m)$ 의 형태를 띠기 때문에 $Z^{[l]}$와 $A^{[l]}$ 모두 $(n^{[l]}, m)$ 의 형태를 가진 행렬이 된다. $dA^{[l]}$, $dZ^{[l]}$ 또한 마찬가지다.
왜 심층 신경망이 필요할까?
심층 신경망이 필요한 이유는 간단하다. 얕은 신경망으로 할 수 없던 더 복잡한 분석을 진행할 수 있기 때문이다.
얼굴 인식 프로그램을 만든다고 생각해보자. 먼저 얼굴 그림에 있는 각종 모서리의 방향과 위치를 파악한다. 그리고 그 분석 데이터를 가지고 눈, 코와 같은 얼굴의 일부를 감지한다. 그 다음에는 다시 그 정보를 가지고 서로 다른 종류의 얼굴을 인식한다. 이처럼 심층 신경망을 이용하면 점점 복잡한 분석을 진행할 수 있다.

음성 데이터 역시 비슷한 과정을 거친다. 먼저 낮은 수준에서 음성을 구분한 뒤, 음소, 단어, 문장 순으로 점점 복잡한 분석을 진행하는 것이다.
심층 신경망의 또다른 장점으로는 계산의 복잡도를 줄일 수 있다는 것에 있다.
비트 연산의 일종인 XOR 연산을 진행한다고 해보자. 얕은 신경망을 이용하면 비트 조합의 모든 가능성을 한 은닉층에서 열거해서 답을 도출해야 하기 때문에 $O(2^n)$ 의 복잡도를 가진다.
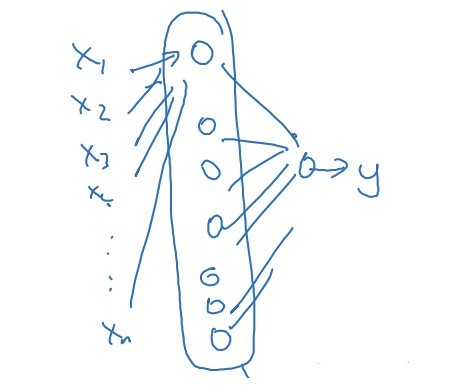
그러나 은닉층이 여러 개인 심층 신경망을 이용하면 단계적인 연산을 수행할 수 있기 때문에 복잡도가 $O(\log{n})$ 으로 개선된다.
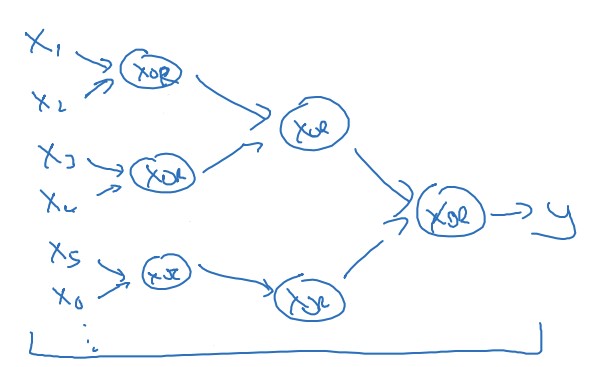
이처럼 심층 신경망은 강력한 장점을 가지고 있다.
심층 신경망 구현하기
심층 신경망을 어떻게 구현하는지 알아보자.
먼저 정방향 전파를 살펴보자. 정방향 전파에서는 $a^{[l - 1]}$ 를 입력으로 받고 $a^{[l]}$ 을 결과로 도출한다. 계산 과정은 몇 번이나 살펴보았듯이 $z^{[l]} = W^{[l]}a^{[l - 1]} + b^{[l]}$, $a^{[l]} = g^{[l]}(z^{[l]})$ 이다. 여기서 $z^{[l]}$ 을 저장해 놓으면 역방향 전파에서 유용하게 사용할 수 있다.
역방향 전파에서는 $da^{[l]}$ 를 입력으로 하고 $da^{[l - 1]}$ 을 출력으로 한다. 그리고 최종적으로는 $dw^{[l]}$, $db^{[l]}$ 을 구한다.
위 과정을 그림으로 표현하면 아래와 같다.
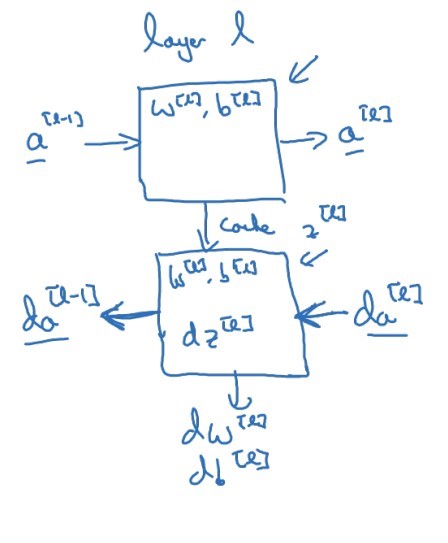
더 자세하게 나타내면 다음과 같다.
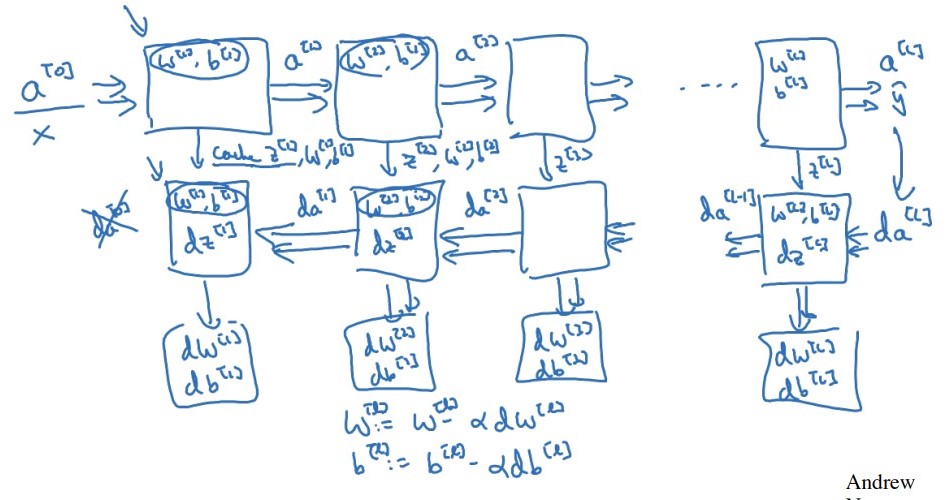
$z^{[l]}$ 뿐만 아니라 $W^{[l]}$, $b^{[l]}$ 도 저장해 놓으면 유용하다. 마지막 $da^{[0]}$ 은 계산해도 쓸모가 없기 때문에 굳이 계산하지 않는다.
정방향 전파와 역방향 전파
심층 신경망에서의 정방향 전파 공식들을 알아보자.
- $Z^{[l]} = W^{[l]}A^{[l - 1]} + b^{[l]}$
- $A^{[l]} = g^{[l]}(Z^{[l]})$
얕은 신경망과 큰 차이가 없다.
역방향 전파 공식도 살펴보자.
- $dZ^{[l]} = dA^{[l]} \odot {g^{[l]}}’(Z^{[l]})$
- $dW^{[l]} = \frac{1}{m} dZ^{[l]}A^{[l - 1]T}$
- $db^{[l]} = \frac{1}{m} np.sum(dZ^{[l]},$ axis= 1, keepdims = True $)$
- $dA^{[l - 1]} = W^{[l]T}dZ^{[l]}$
역시 얕은 신경망과 비슷하다.
Hyperparameter
초매개변수(Hyperparameter)는 매개변수(w, b)를 결정 짓는 변수들을 말한다. 예를 들자면 학습률 $\alpha$ , 경사하강법 반복 횟수, 은닉층 개수, 은닉층 유닛의 개수, 활성화 함수 등이 있다.
초매개변수는 매개변수에 영향을 주기 때문에, 적절한 초매개변수를 설정하는 것은 매우 중요하다. 그러나 처음부터 완벽한 초매개변수를 설정하기란 여간 쉬운 것이 아니다. 또한, 학습 모델을 구현하는 환경(ex. CPU, GPU)에 따라 적절한 초매개변수가 바뀔 수도 있다.
따라서 다양한 초매개변수를 여러 번 시도해보면서 시행착오 끝에 가장 적절한 것을 경험적으로 선택하는 수밖에 없다. 물론 머신러닝 분야가 빠르게 발전하고 있기에 곧 적절한 초매개변수를 선정하는 효율적인 과정이 개발될 수도 있을 것이다.
인간의 뇌와 심층 신경망
대중에게 머신러닝을 알기 쉽게 설명하는 영상이나 뉴스 기사 등을 보면 신경망을 인간의 뇌에 비유하는 것을 어렵지 않게 볼 수 있다.
그러나 인간의 뇌와 신경망은 사실 관련이 많지 않다.
생명과학자들은 신경의 기본 단위인 뉴런의 기본 구조를 밝히고 그 생물학적 작동 기작을 설명하는 데까지는 성공했다. 그러나 아직 하나의 뉴런이 사고 과정에서 수행하는 역할에 대해 완벽히 이해하지는 못했으며, 인간의 뇌에 대한 이해 또한 마찬가지이다. 따라서 그 사고 과정을 이해하지도 못한 뇌를 머신러닝에 비유하는 것은 무리가 있다.

댓글남기기