신경망의 표현
신경망은 앞선 강의들에서 보았던 연산을 수행하는 여러 층으로 나누어져 있다고 이해하면 된다. 데이터 x들이 입력되면 신경층(Layer)을 거쳐 결과를 도출한다. 이전 신경츨에서 계산된 결과가 다음 신경층을 계산하는 입력으로 사용된다.
신경망의 기본적인 구조는 아래와 같다.
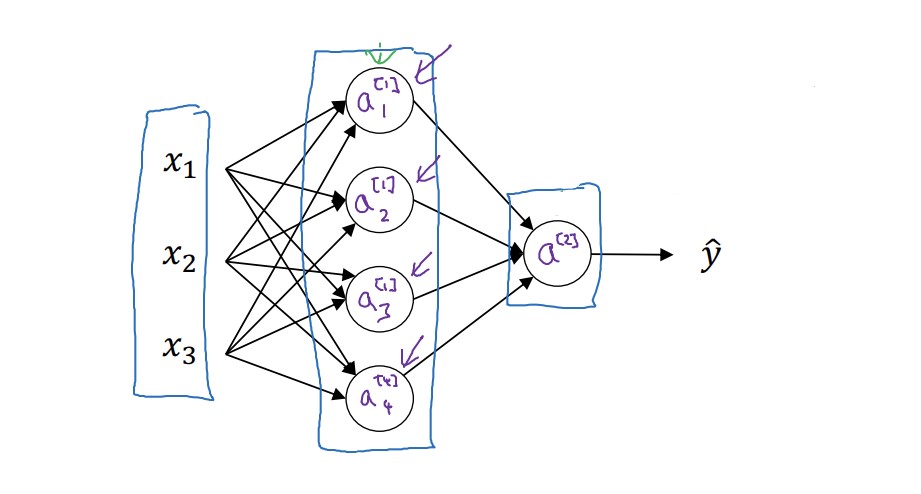
가장 왼쪽에 위치하는 x들은 입력층(Input Layer)이다. 행렬로 X라고 쓰기도 하지만, 0번째 신경층이라는 의미로 $a^{[0]}$ 이라고 표현하기도 한다. 보통 대괄호를 이용해서 신경층을 표현하고, 소괄호를 이용해서 몇 번째 훈련 데이터인지를 나타낸다. 아래첨자는 몇 번째 노드인지를 가리킨다.
다음 층은 은닉층(Hidden Layer)이다. 은닉층은 훈련 데이터와 결과에는 나타나지 않는다. 중간 계산 과정인 것이다. $a^{[1]}$ 로 표현한다. 첫번째 은닉층에서 사용되는 매개변수 W(행렬)와 b 역시 위 첨자를 이용해서 $W^{[1]}, b^{[1]}$ 로 나타내기도 한다. 위 예시에서 W는 (4, 3), b는 (4, 1)의 모양이다. 앞은 은닉층 노드의 개수, 뒤는 입력층 노드의 개수이다.
결과층(Output Layer)는 하나의 노드로 이루어져 있다. 여기 역시 계산에 사용되는 $W^{[2]}, b^{[2]}$ 가 있으며, 각각 (1, 4), (1, 1)의 형태이다.
위 예시는 2개의 층으로 구성된 신경망으로 표현한다. 입력층은 층을 셀 때 포함하지 않는 것이다.
신경망 결과 계산하기
하나의 노드는 다음과 같이 나타낼 수 있다.
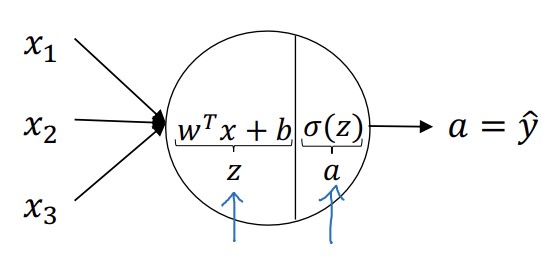
먼저 선형회귀를 계산하고, 그 다음에 시그모이드 함수에 대입하는 과정으로 나눈 것이다. 이러한 노드들이 여러개 모인 것이 하나의 신경층이다. 즉, 첫 번쨰 노드와 두 번째 노드에서는 다음과 같은 계산이 진행된다.
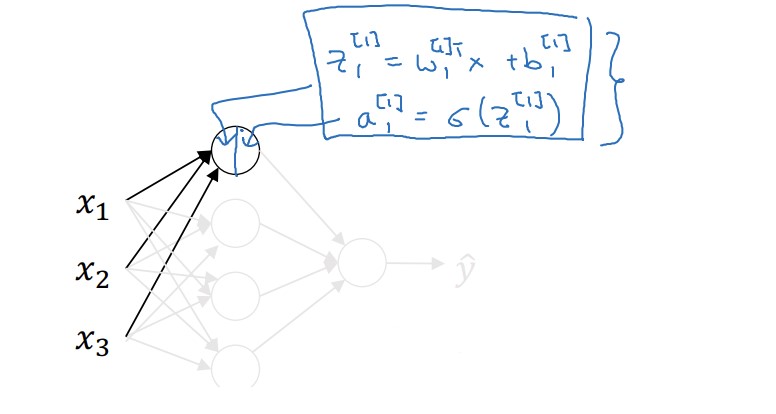
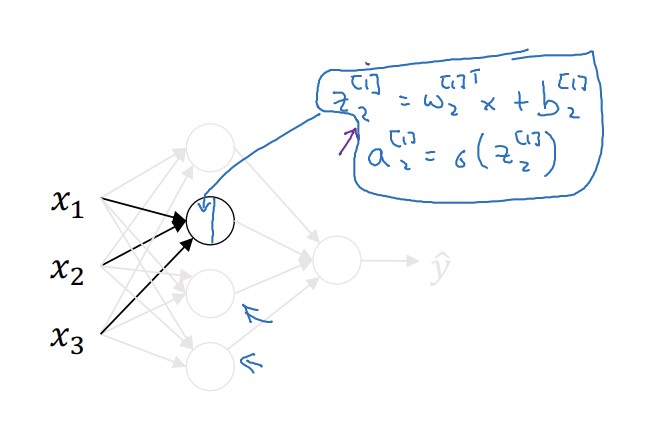
만약 이 과정을 프로그래밍 한다면 반복문을 사용하는 것이 가장 단순한 방법일 것이다. 그러나 우리는 앞에서 벡터화의 유용성을 보았다. 4개의 노드에서 진행되는 다음과 같은 계산 과정을 벡터화 할 것이다.
\[z_1^{[1]} = w_1^{[1]T}x + b_1^{[1]}, \; a_1^{[1]} = \sigma(z_1^{[1]})\] \[z_2^{[1]} = w_2^{[1]T}x + b_2^{[1]}, \; a_2^{[1]} = \sigma(z_2^{[1]})\] \[z_3^{[1]} = w_3^{[1]T}x + b_3^{[1]}, \; a_3^{[1]} = \sigma(z_3^{[1]})\] \[z_4^{[1]} = w_4^{[1]T}x + b_4^{[1]}, \; a_4^{[1]} = \sigma(z_4^{[1]})\]방법은 앞선 강에서 본 것과 동일하다. w를 행렬 W로, x를 벡터로 묶으면 된다.
\[z^{[1]} = \begin{bmatrix} - & w_1^{[1]T} & - \\ - & w_2^{[1]T} & -\\- & w_3^{[1]T} & - \\ - & w_4^{[1]T} & - \end{bmatrix} \begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix} + \begin{bmatrix}b_1^{[1]}\\b_2^{[1]}\\b_3^{[1]}\\b_4^{[1]}\end{bmatrix} = \begin{bmatrix} w_1^{[1]T}x + b_1^{[1]}\\ w_2^{[1]T}x + b_2^{[1]}\\w_3^{[1]T}x + b_3^{[1]}\\ w_4^{[1]T}x + b_4^{[1]} \end{bmatrix} = \begin{bmatrix}z_1^{[1]}\\z_2^{[1]}\\z_3^{[1]}\\z_4^{[1]}\end{bmatrix}\]결과로 얻은 z를 시그모이드 함수에 적용하면 $a^{[1]}$을 얻을 수 있다.
따라서 다음과 같은 신경망에 벡터화를 적용하면 반복문이 필요하지 않다.
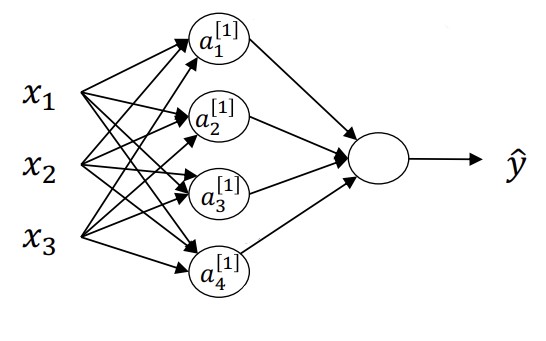
계산 과정: \(z^{[1]} = W^{[1]}a^{[0]} + b^{[1]} \\ a^{[1]} = \sigma(z^{[1]}) \\ z^{[2]} = W^{[2]}a^{[1]} + b^{[2]} \\ a^{[2]} = \sigma(z^{[2]})\)
여러 개의 훈련데이터에 벡터화
훈련데이터가 m개라면 어떻게 할까? 아직 벡터화가 익숙치 않다면 다시 위에서 본 마지막 과정을 m번 반복할 생각을 하고 있을 것이다.인간은 쉽게 바뀌지 않는다 다시 말하지만, 벡터화가 유용하다.
매우 쉽다. x를 벡터로 묶었다면 이번에는 행렬로 묶으면 된다. 다음처럼 말이다.
\[X = \begin{bmatrix}| & | & & |\\ x^{(1)} & x^{(2)} & \cdots & x^{(m)}\\| & | & & |\end{bmatrix}\]위 식에 똑같이 넣고 계산하면 다음과 같은 결과들이 나온다.
\[Z^{[1]} = \begin{bmatrix}| & | & & |\\ z^{[1](1)} & z^{[1](2)} & \cdots & z^{[1](m)}\\| & | & & |\end{bmatrix}\] \[A^{[1]} = \begin{bmatrix}| & | & & |\\ a^{[1](1)} & a^{[1](2)} & \cdots & a^{[1](m)}\\| & | & & |\end{bmatrix}\]가로 개수는 훈련 데이터의 개수, 세로는 은닉층 노드의 개수를 뜻한다.
m개의 훈련데이터에 대한 벡터화를 이용한 계산 과정을 살펴보자.
\[Z^{[1]} = W^{[1]}A^{[0]} + b^{[1]} \\ A^{[1]} = \sigma(Z^{[1]}) \\ Z^{[2]} = W^{[2]}A^{[1]} + b^{[2]} \\ A^{[2]} = \sigma(Z^{[2]})\]여러가지 활성화 함수
지금까지는 계산의 마지막에 시그모이드 함수를 사용했지만 사실 교수님은 시그모이드 함수를 거의 사용하지 않는다고 한다. 뭐지
시그모이드 함수 대신 사용하는 함수는 tanh 함수이다. tanh 함수 다음과 같다. \(a = \tanh{z} = \frac{e^z - e^{-z}}{e^z + e^{-z}}\)
tanh 함수는 원점을 중심으로 대칭이며, 원점을 지난다. 따라서 0.5를 기준으로 대칭이었던 시그모이드 함수와는 다르게 데이터들의 평균값을 0에 가깝게 조정할 수 있다는 장점이 있다.
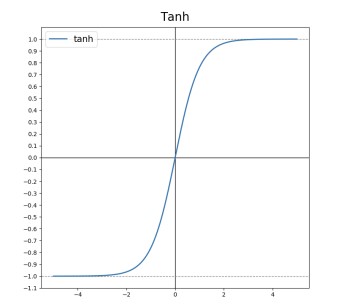
보편적으로는 시그모이드 함수 대신 tanh 함수를 더 많이 사용한다. 그러나 마지막 결과층을 도출할 때 한해서 시그모이드 함수를 주로 사용하는데, $y$가 0 또는 1 인 경우 $\hat{y}$ 역시 0과 1 사이인 것이 계산에 용이하기 때문이다.
그러나 시그모이드 함수와 tanh 함수 모두 단점이 있다. 바로 z값이 매우 크거나 매우 작으면 그 지점에서의 기울기가 감소하고, 이로 인해 경사하강법이 느려진다는 것이다. 이를 보완하기 위해 ReLU 함수를 사용한다.
ReLU 함수는 다음과 같이 생겼다.
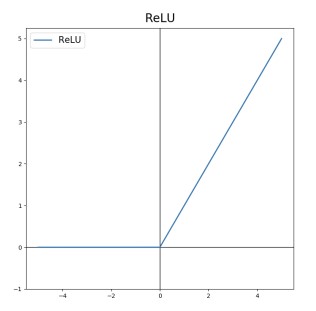
표기는 $a = max(0, z)$ 이다. 0과 z 중에 더 큰 값을 함숫값으로 한다는 뜻이다.
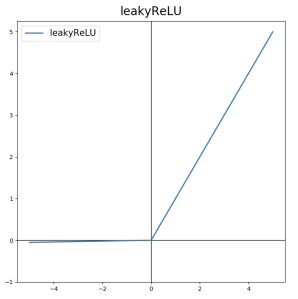
ReLU 함수는 원점에서 미분이 불가능하다. 따라서 원점에서는 경사하강법을 적용할 수 없다. 그러나 z가 0이 되는 경우는 극히 드물기 때문에 큰 문제 없이 널리 사용된다. 0보다 작은 구간에서 도함수가 0인 것을 보완하기 위한 Leaky ReLU($a = max(0.01z, z)$) 함수도 있다.
비선형 활성화 함수가 필요한 이유
ReLU, tanh, 시그모이드 함수 등은 비선형함수이다. 왜 비선형함수를 사용할까?
선형함수를 이용해서 은닉층들을 통과하는 과정을 생각해보자. 다음과 같은 계산 과정으로 진행된다.
\[a^{[1]} = z^{[1]} = W^{[1]}x + b^{[1]} \\ a^{[2]} = z^{[2]} = W^{[2]}a^{[2]} + b^{[2]}\] \[a^{[2]} = W^{[2]}(W^{[1]}x + b^{[1]}) + b^{[2]}\\ = (W^{[2]} + W^{[1]})x + (W^{[2]}b^{[1]} + b^{[2]}) \\ = W'x + b'\]선형함수를 이용해서 계산하면 그 결과 역시 선형함수 식이 도출된다는 것을 알 수 있다. 즉, 선형함수만을 은닉층에 이용한다면 더 깊이있는 계산을 할 수 없고, 은닉층이 없는 것과 다를 바 없는 상황이 펼쳐진다.
예를 들어, $g(z) = z$라는 선형함수를 생각해보자. $g(g(g(z))) = z$처럼 아무리 합성해도 z 이외의 값이 나오지 않는 것을 확인할 수 있다.
다양한 활성화 함수의 도함수
여기서는 다양한 활성화 함수의 도함수를 짚고 넘어간다. 계산 과정은 미적분학 책을 참고하면 금방 알 수 있으니 중요한 포인트 위주로 확인한다.
먼저, 시그모이드 함수이다.
\[g(z) = \sigma(z)= \frac{1}{1 + e^{-z}}\\ g'(z) = \frac{1}{1 + e^{-z}} (1 - \frac{1}{1 + e^{-z}}) \\ = g(z)(1-g(Z))\\ = a(1 - a)\]시그모이드 함수는 도함수를 원래 함수 식으로 표현할 수 있다. 결과 값을 알면 미분계수를 빠르게 구할 수 있다는 장점이 있다.
다음은 tanh 함수이다. \(g(z) = \tanh{(z)} = \frac{e^z - e^{-z}}{e^z + e^{-z}}\\ g'(z) = 1 - (\tanh{(z)})^2 = 1-a^2\)
tanh 역시 원래 함수로 도함수를 나타낼 수 있다.
ReLU와 Leaky ReLU는 상대적으로 매우 간단한 도함수를 가진다.
-
ReLU
$g(z) = max(0, z)$
$g’(z)= \begin{cases} 0,\;if\;z<0
1,\;if\;z\geq0 \end{cases}$ -
Leaky ReLU
$g(z) = max(0.01z, z)$
$g’(z)= \begin{cases} 0.01,\;if\;z<0
1,\;if\;z\geq0 \end{cases}$
원래 두 함수 모두 $z = 0$ 일 때는 미분이 수학적으로 정의되지 않는다. 그러나 z가 0일 확률이 매우 적기도 하고, 큰 문제가 없기 때문에 0에서는 그냥 1로 정의한다.
신경망에서의 경사하강법
입력층의 차원이 $n^{[0]}$, 은닉층의 차원이 $n^{[1]}$, 출력층의 차원이 $n^{[2]}$ 이라고 하자. 먼저, 각종 요소들을 정의한다.
- 매개변수: $w^{[1]}(n^{[1]},\,n^{[0]}),\,b^{[1]}(n^{[1]},\,1),\,w^{[2]}(n^{[2]},\,n^{[1]}),\,b^{[2]}(n^{[1]},\,1)$
- 비용함수: $\displaystyle J(w^{[1]}, b^{[1]}, w^{[2]}, b^{[2]}) = \frac{1}{m}\sum_{i = 1}^{n}{L(\hat{y}, y)}$ ($\hat{y}$ 은 $a^{[2]}$ 로 봐도 됨.)
이 인자들을 가지고, 경사하강법에서는 변수를 0이 아닌 값으로 초기화한 뒤에 다음 과정을 반복한다.
\[dw^{[1]} = \frac{dJ}{dw^{[1]}},\,db^{[1]} = \frac{dJ}{db^{[1]}}\] \[W^{[1]} = W^{[1]} - \alpha W^{[1]}\] \[b^{[1]} = b^{[1]} - \alpha b^{[1]}\] \[...\]계산 그래프에서 오른쪽으로 진행하는 정방향 전파(Forward Propagation)와 왼쪽으로 진행하는 역방향 전파(Back Propagation)에서 사용되는 공식을 정리하면 다음과 같다.
- 정방향 전파
- $Z^{[1]} = W^{[1]}X + b^{[1]}$
- $A^{[1]} = g^{[1]}(Z^{[1]})$
- $Z^{[2]} = W^{[2]}A^{[1]} + b^{[2]}$
- $A^{[2]} = g^{[2]}(Z^{[2]}) = \sigma{(Z^{[2]})}$
- 역방향 전파
- $dZ^{[2]} = A^{[2]} - Y$
- $dW^{[2]} = \frac{1}{m} dZ^{[2]}A^{[1]T}$
- $db^{[2]} = \frac{1}{m} np.sum(dZ^{[2]},$ axis= 1, keepdims = True $)$
- $dZ^{[1]} = W^{[2]T}dZ^{[2]} \odot {g^{[1]}}’(Z^{[1]})$ ($\odot$ 은 elementwise product)
- $dW^{[1]} = \frac{1}{m} dZ^{[1]}X^T$
- $db^{[1]} = \frac{1}{m} np.sum(dZ^{[1]},$ axis= 1, keepdims = True $)$
유도는 앞선 강의부터 살펴본 공식들과 미적분학의 지식을 조금 사용해서 할 수 있다. 로지스틱 회귀로 먼저 공식의 기본적인 구조를 구하고, 신경망 경사하강법에 그 공식을 적용하면 조금 더 쉽다. 자세한 유도과정은 강의자료를 참고하자. 사실 유도과정을 몰라도 상관 없다고 한다
변수의 랜덤 초기화
매개변수를 0으로 초기화하면 안된다고 살짝 언급했다. 왜 그럴까?

위와 같은 간단한 신경망이 있다고 가정하자. 은닉층에서 W와 b를 다음과 같이 정의했다.
\[W^{[1]}= \begin{bmatrix}0 & 0\\0 & 0 \end{bmatrix},\, b^{[1]} = \begin{bmatrix}0\\0\end{bmatrix}\]그러면 정방향 전파에서 $a_1^{[1]} = a_2^{[1]}$ 가 된다. 매개변수가 똑같기 때문에 벌어지는 일이다. 마찬가지로 역방향 전파에서도 $dz_1^{[1]} = dz_2^{[1]}$ 가 된다.
이런 상황에서 가운데에 있는 은닉층의 유닛들은 모두 동일해지게 된다. 이를 ‘Symmetric’이라고 표현한다. 경사하강법을 몇 번 반복하든 간에, 은닉층은 모두 symmetric한 상태에 있으며, 학습을 수행하는 의미가 없어지게 된다. 그래서 매개변수를 0이 아닌 값으로 초기화하는 것이 매우 중요하다.(사실 b만 0인 것은 상관 없다. w가 0이 아니어야 한다.)
다음은 변수를 초기화하는 일련의 코드이다.
W^[1] = np.random.randn((2, 2)) * 0.01 # elementwise
b^[1] = np.zeros((2, 1))
W^[2] = np.random.randn((1, 2)) * 0.01 # elementwise
b^[2] = 0
왜 굳이 0.01을 사용하는지 의문이 들 수도 있다. 함수의 모양을 생각해보면 그 답이 나온다. W의 값이 너무 크면 Z의 값들이 매우 크거나 매우 작아질 것이다. 이는 tanh나 시그모이드 함수 양 끝으로 이동하게 하고, 경사하강법이 매우 느려지는 결과를 유발한다. 학습이 지나치게 느려지는 것을 방지하기 위해 작은 값인 0.01을 사용한다.
별도의 출처가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기