이진 분류
64픽셀 $\times$ 64픽셀 크기의 사진이 있다고 가정해보자. 우리가 원하는 것은 이 사진을 분석해서 피사체가 고양이인지 아닌지를 구별하는 것이다.

색상은 기본적으로 RGB로 이루어져 있기 때문에 아래와 같은 정보를 얻게 된다.
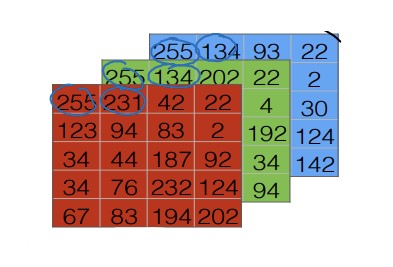
이를 특성벡터로 변환해야 분석에 사용할 수 있다. 특성벡터는 말 그대로 특성을 담고있는 벡터를 의미한다.
\[x=\begin{bmatrix}255\\231\\...\\...\\255\\134 \end{bmatrix}\]특성벡터의 차원(dimension)을 확인하는 것은 중요하다. 3개의 색상이 각각 64 $\times$ 64 의 픽셀을 가지고 있으므로 아래와 같이 계산할 수 있다.
\[n = n_x = 64 \times 64 \times 3 = 12288\]앞으로 $n_x$는 벡터 $x$의 차원을 표현하는 것으로 약속한다.
특성벡터($x$)와 결과($y$)의 조합인 $(x, y)$ 는 다음과 같은 조건을 따른다.
- $x \in R^{n_x}$ (n차원 벡터 집합)
- $y \in {0, 1}$
m개의 훈련 데이터가 있다고 하면 다음과 같이 표현된다.
\[\{(x^{(1)}, y^{(1)}), (x^{(2)}, y^{(2)}), ... , (x^{(m)}, y^{(m)})\}\]여기서 m개의 특성벡터만을 모아 표현할 수도 있다.
\[X = \begin{bmatrix} | & | & & |\\ x^{(1)} & x^{(2)} & \cdots & x^{(m)}\\ | & | & & | \end{bmatrix}\]행렬 X의 모양은(X.shape) $(n_x, m)$이다. 벡터 m개를 모아두었고, 각각의 벡터가 $n_x$차원을 가지기 때문이다.
결과인 y도 행렬로 표현할 수 있다.
\[Y=\begin{bmatrix}y^{(1)}&y^{(2)}&...&y^{(m)}\end{bmatrix}\]모양은 X와 비슷하지만 실제로는 완전히 다르다. Y.shape의 값은 $(1, m)$이다.
로지스틱 회귀
특성벡터 x가 주어졌을 때 우리는 결과 y를 알고 싶다. 더 자세하게는 그 그림에 찍힌 것이 진짜 고양이인 확률을 알고 싶은 것이다. 식으로 표현하면 아래와 같다.
\[\hat{y} = P(y=1|x)\]일종의 조건부 확률이다.
x를 이용해 y를 도출하는 과정에서는 다양한 매개변수가 필요하다. w와 b가 그 역할을 해준다.
$w \in R^{n_x}$
$b \in R$
w는 벡터이고 b는 실수이다. 결과 값을 구하는 과정을 w, x, b를 이용해 선형회귀처럼 식을 써보면 아래와 같다.
\[\hat{y} = w^Tx + b\]그러나 앞서 다른 강의에서 살펴보았듯이, 선형회귀는 확률을 예측하는 데 적합하지 않다. 확률은 0과 1 사이의 값이어야 하지만, 선형회귀의 결과는 0보다 작을 수도 있고, 1보다 클 수도 있기 때문이다.
그래서 우리는 로지스틱 회귀를 사용한다. 로지스틱 회귀는 시그모이드 함수를 이용해 선형회귀의 결과를 0과 1 사이로 fitting하는 것이라고 생각하면 편하다. 시그모이드 함수는 아래처럼 생겼다.
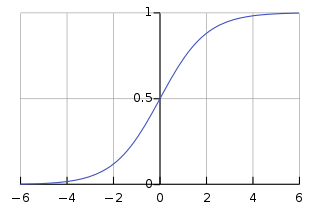
보다시피 시그모이드 함수는 모든 함숫값이 0과 1 사이에 위치한다. 어떠한 값을 집어넣어도 0과 1사이의 결과 값이 주어진다.
앞선 식을 시그모이드 함수에 적용하면 다음과 같다.
\[\hat{y} = \sigma(w^Tx + b)\]시그모이드 함수식은 이렇게 생겼다.
\[\sigma(z) = \frac{1}{1+e^{-z}}\]z가 매우 커지면 $e^{-z}$는 0에 가까워지고, 함숫값은 1에 가까워진다. 반대로 z가 매우 작아지면 $e^{-z}$는 매우 커지고, 함숫값은 0에 가까워진다.
손실함수와 비용함수
로지스틱 회귀는 말 그대로 ‘예측’이다. 우리는 예측이 실제와 차이가 없도록 각 특성벡터들에 대해 실제 결과와 예측값의 차이를 줄이고 싶다.
손실함수(loss function)은 하나의 특성벡터에 대해 결과와의 차이를 파악하는 함수이다. ‘로지스틱 회귀에서’ 손실 함수는 다음과 같이 정의한다.
\[L(\hat{y}, y) = -(y\log{}{\hat{y}} + (1-y)\log{}{(1-\hat{y})})\]y가 1이면, 손실함수는 $ L(\hat{y}, y) = -\log{}{\hat{y}} $ 가 되고, $\hat{y}$ 가 증가해야 손실이 줄어든다.
반대로 y가 0이면 손실함수는 $ L(\hat{y}, y) = -\log{}{(1-\hat{y})} $ 가 되고, $\hat{y}$ 가 감소해야 손실이 줄어든다.
손실함수가 하나의 특성벡터에 대해 손실을 파악한다면, 비용함수(cost function)는 전체 행렬에 대한 차이를 파악한다.
\[\displaystyle J(w, b) = \frac{1}{m} \sum_{i=1}^{m}{L(\hat{y}^{(i)}, y^{(i)})} = -\frac{1}{m} \sum_{i=1}^{m}{[y^{(i)}\log{}{\hat{y}^{(i)}} + (1-y^{(i)})\log{}{(1-\hat{y}^{(i)})}]}\]비용함수가 가진 변수에 주목하자. 핵심은 손실함수를 최소화하는 w와 b를 찾는 것이다.
경사하강법
경사하강법은 비용함수를 최소화하는 매개변수 w, b를 찾는 과정이다. 함수로 만들어진 면 위의 임의의 한 점에서 최솟값을 향해 하강한다고 하여 경사하강법이라는 이름이 붙었다.
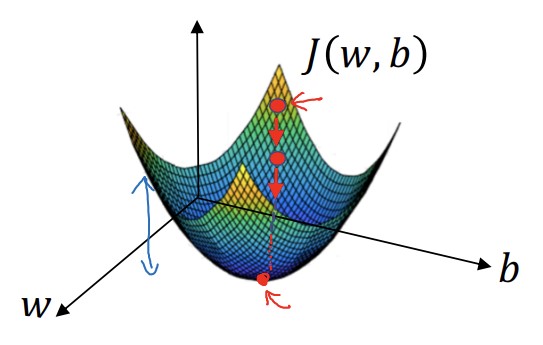
위의 그림에서 면 위에 있는 점의 함숫값이 $J(w, b)$ 이다. 우리는 면 위에서 임의로 점을 하나 선택한 뒤, 가장 낮은 곳을 향해 빠르게 내려올 것이다. 비용함수를 최소화하고 싶기 때문이다.
어떻게 가장 빠르게 하산할 수 있는 방법을 찾을까? 바로 기울기를 활용하면 된다. 우리는 기울기를 활용해 w와 b를 변경함으로써 최적의 값을 찾는다.
가장 간단하게 살펴보자. 다음과 같은 w에 대한 아래로 볼록한 함수가 있다.
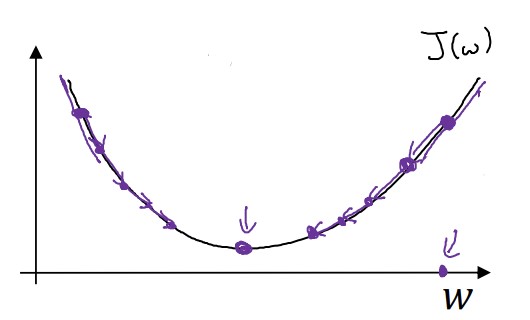
만약 우리가 잡은 점이 최저점의 오른쪽에 있다면, 그 점에서의 기울기는 양수가 될 것이다. 기울기가 양수라면, 왼쪽으로 내려오면 된다. 반대로 우리가 잡은 점이 최저점의 왼쪽에 있다면, 그 점에서의 기울기는 음수이다. 그럼 기울기가 음수가 아닐때까지(0이 될 때까지) w를 증가시키면 된다.
위에서 살펴본 과정은 다음 식처럼 나타낼 수 있다. 아래의 식을 w가 더 이상 변하지 않을 떄까지 반복한다.
\[w = w -\alpha\frac{dJ(w)}{dw}\]$\alpha$ 는 학습률(learning rate)를 의미한다. 학습률이 클수록 더 빠르게 w가 변화할 것이라고 생각할 수 있다. $\frac{dJ(w)}{dw}$ 는 고등학교에서 살펴본 바로 그 미분계수이다. 여기서는 함수의 변수가 하나지만, 실제 비용함수는 w, b 두 개의 변수를 가진다. 그래서 미분계수도 ‘편미분계수’을 활용해야 한다.
\[w = w -\alpha\frac{dJ(w, b)}{dw}\] \[b = b -\alpha\frac{dJ(w, b)}{db}\]엄밀하게는 편미분계수를 표현할 때 $\partial$ 을 활용해야하지만, 큰 상관은 없다.
cf. 손실함수 더 알아보기
로지스틱 회귀에서 사용하는 손실함수는 일반적으로 사용하는 손실함수와는 다르다. 일반적인 손실함수는 아래와 같다. \(L(\hat{y}, y) = \frac{1}{2}(\hat{y} - y)^2\) 그러나 이는 최적값 1개를 찾아야 하는 로지스틱 회귀에는 부적절하다. 지역 최적값이 전역최적값이 아닐 수 있기 때문이다(추가 설명 링크).
반면 위에서 소개한 손실함수는 아래로 볼록한 모양으로 전역최적이 지역최적과 일치한다. 그래서 우리는 일반적인 손실함수 대신 다른 손실함수를 활용한다.
미분
고등학교에서 더 어려운 것도 했다. 생략.
계산 그래프와 미분계수
계산 그래프는 계산 과정을 나타낸 일종의 그림으로 보면 된다. 다음과 같은 식을 계산 그래프로 계산한다고 해보자.
\[J(a, b, c) = 3(a + bc)\]계산 순서대로의 결과를 u, v, J를 이용해 나타낼 수 있다.
\(u = bc\)
\(v = a + u\)
\(J = 3v\)
이 계산 과정을 계산 그래프로 나타내면 다음과 같다.
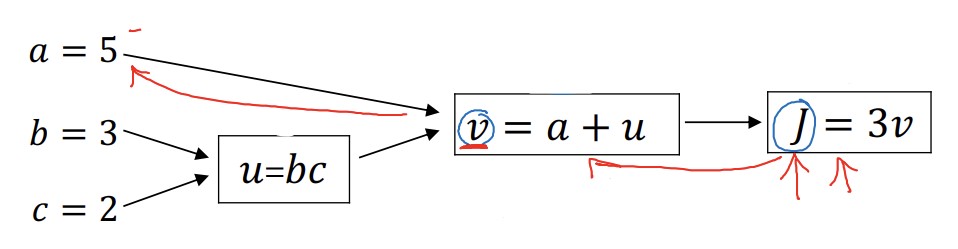
로지스틱 회귀와 경사하강법에서는 계산 그래프를 사용해 얻을 수 있는 장점이 있다. 위 그림에서 빨간색 화살표를 따라 계산 그래프를 역(오른쪽 -> 왼쪽)으로 추적하여 미분계수를 쉽게 구할 수 있다.
그럼 미분계수를 구해보자. 가장 오른쪽부터 시작하므로, $\frac{dJ}{dv}$ 부터 구한다. $J=3v$ 이므로 $\frac{dJ}{dv} = 3$ 이다.
그 다음에는 $\frac{dJ}{da}$ 를 구한다. 연쇄법칙을 사용하면 되는데, $\frac{dJ}{da} = \frac{dJ}{dv} \cdot \frac{dv}{da}$ 이므로 $\frac{dJ}{da}=3$ 이다. $\frac{dJ}{du}$ 도 똑같이 구하면 된다.
마지막으로 $\frac{dJ}{du}$ 를 구해보자. 연쇄법칙을 사용하면 $\frac{dJ}{db} = \frac{dJ}{du} \cdot \frac{du}{db}$ 가 된다. $\frac{dJ}{du}=3$ 이고, $\frac{du}{db}$ 가 c(c=2)이므로 $\frac{dJ}{db}=6$ 이다.
로지스틱 회귀와 경사하강법에 계산 그래프 적용하기
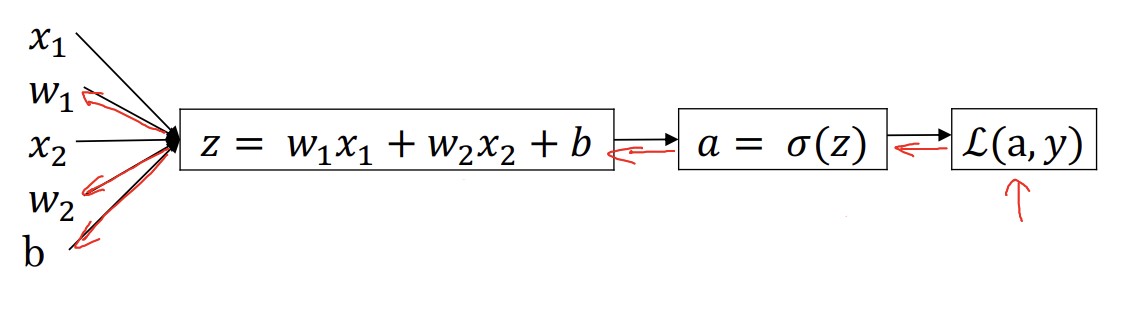
여기서도 마찬가지로 오른쪽부터 시작한다. $\frac{dL(a, y)}{da}$ 를 계산하면 $-\frac{y}{a} + \frac{1-y}{1-a}$ 가 된다(잘 모르겠으면 미적분학 책을 뒤져보자.).
다음 과정은 손실함수 $\frac{dL(a, y)}{dz}$ 를 구하는 것이다.
\(\frac{dL(a, y)}{dz} = \frac{dL}{da} \cdot \frac{da}{dz}\) \(\frac{dL(a, y)}{dz} = (-\frac{y}{a} + \frac{1-y}{1-a}) \cdot a(1-a)\) \(\frac{dL(a, y)}{dz} = a - y\)
마지막으로는 $\frac{dL}{dw_1}$, $\frac{dL}{dw_2}$, $\frac{dL}{db}$ 를 구한다. 각각 $(x_1 \cdot \frac{dL}{dz})$ , $(x_2 \cdot \frac{dL}{dz})$ , $\frac{dL}{dz}$ 이다.
프로그래밍에서 미분계수를 변수로 사용해야 할 때가 많다. 그러나 그 떄마다 분수로 표현할 수도 없고, 파이썬에서는 분수 형식의 변수를 지원하지도 않는다.
$\frac{dFindOutputVar}{dvar}$ 을dJdvar처럼 쓸 수도 있지만, 편의상dvar이라고 적는 경우가 더 많다. $\frac{dL}{da}$ 는da, $\frac{dL}{dw_1}$ 은dw1이 되는 식이다.
m개의 학습 데이터에 대한 경사하강법
지금까지는 하나의 학습 데이터에 대해 어떻게 경사하강법을 적용하는지를 보았다. 이제는 m개의 데이터에 적용하는 것을 살펴볼 것이다.
우리는 비용함수를 $\displaystyle J(w, b) = \frac{1}{m} \sum_{i=1}^{m}{L(\hat{y}^{(i)}, y^{(i)})}$ 와 같이 쓴다. 비용함수를 미분하면 아래와 같이 쓸 수 있다.
\[\displaystyle \frac{d}{dw_1}J(w, b) = \frac{1}{m} \sum_{i=1}^{m}{\frac{d}{dw_1}L(\hat{y}^{(i)}, y^{(i)})}\]$\frac{d}{dw_1}L(\hat{y}^{(i)}, y^{(i)})$ 는 $d{w_1}^{(i)}$ 로 표현할 수도 있다.
본격적으로 반복문을 살펴보자. 아래 반복문은 경사하강법을 1회 시행했을 때이다.
J = 0; dw1 = 0; dw2 = 0; db = 0
for i = 1 to m
z(i) = w^T * x(i) + b
a(i) = sigmoid(z(i))
J += -[y(i)log(a(i)) + (1 - y(i))log(1-a(i))]
dz(i) = a(i) - y(i)
# n개의 특성에 대해 다시 반복해야하는 부분
dw1 += x1(i)dz(i)
dw2 += x2(i)dz(i)
db += dz(i)
J /= m
dw1 /= m
dw2 /= m
db /= m
위 의사코드를 하나씩 살펴보자. 먼저, m개의 훈련세트이므로 m번 반복하는 for문이 있다. 반복문에서 가장 먼저 하는 것은 선형회귀식에 $x^{(i)}$ 를 대입하는 것이다. 그리고 이를 다시 시그모이드 함수에 넣어 그 결과를 $a^{(i)}$ 에 대입한다. $a^{(i)}$ 는 손실함수 계산에 사용된다. 그리고 손실함수 계산 결과를 변수 J에 넣는다. 이름에서 느낌이 오듯이 J는 나중에 비용함수 계산에 사용될 것이다.
그 다음 단락은 특성의 개수에 따라 달라진다. 특성에 따라 미분계수를 구하는 과정으로, 특성이 n개면 n번 반복한다.
마지막 단락에서는 이렇게 구한 값들을 m으로 나눈다. 이제 J는 비용함수의 값을 나타내게 되었다.
최종적으로 $w_1$, $w_2$, b를 정리하면 아래와 같다. $\alpha$ 는 학습률이다.
\[w_1 = w_1 - \alpha dw_1\] \[w_2 = w_2 - \alpha dw_2\] \[b = b - \alpha db\]위 과정은 경사하강법 1회 수행에 해당한다. 경사하강법을 n번 반복하여 최적의 값을 찾았다면, 위 과정을 n번 반복한 것이다.
위 과정의 가장 큰 단점은 반복문이 두 번 들어간다는 것이다. 반복문이 많아지면 당연히 수행 속도가 느려진다. 벡터화를 사용하면 명시적인 반복문을 제거할 수 있다. 과거에는 벡터화가 액세서리처럼 있으면 좋고 없어도 나쁠 것 없는 요소였지만, 딥러닝이 점점 고도화되는 현재는 필수적인 요소로 자리잡았다.
별도의 출처가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기