Softmax 함수
분류에서 우리가 알고 싶은 것은 각 항목에 속할 ‘확률’일 것이다. 따라서 가설 함수의 결과로 터무니 없이 큰 수가 나오는 것보다, 결과 vector의 모든 요소를 합했을 때 1이 나오도록 바꾸어 주는 것이 좋다. 그 역할을 softmax 함수가 한다.
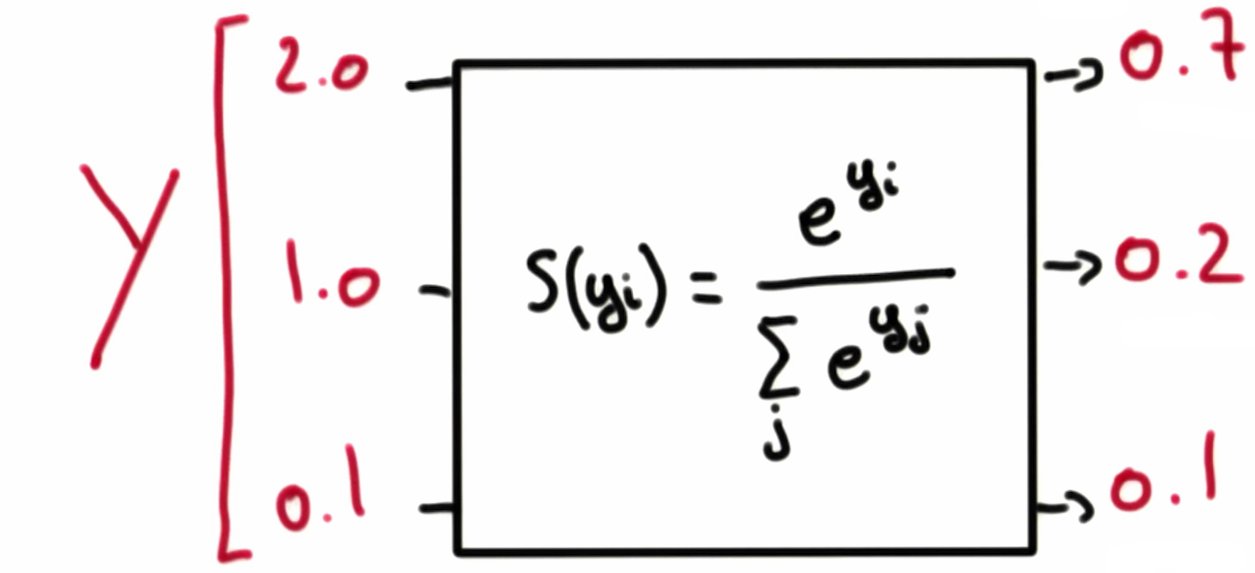
Softmax 함수식은 다음과 같다.
\[S(y_i) = \frac{e^{y_i}}{\displaystyle \sum_{j}{e^{y_i}}}\]Softmax 함수를 통해 각 클래스에 속할 확률을 구했다면, 가장 높은 확률을 가진 클래스를 선택하면 된다. 이 과정은 원-핫 인코딩이 담당한다(텐서플로에서는 argmax()를 이용해서 하면 된다).
Softmax의 비용함수
Softmax 함수의 비용함수는 cross-entropy를 사용한다. 식은 다음과 같다.
\[D(S, L) = - \displaystyle \sum_{i}{L_i \log{(S_i)}}\]위 식에서 $L_i \log{(S_i)}$ 연산은 elementwise 곱이며, 시그마는 해당 결과 vector의 요소들을 더하라는 의미이다. 위 식을 조금 변형하여 자세히 이해해보자.
\[\displaystyle - \sum_{i}{L_i \log{(\hat{y}_i)}} = \displaystyle \sum_{i}{L_i \odot (-\log{(\hat{y}_i)})}\]어차피 softmax 함수의 영향으로 인해 $\hat{y}_i$ 는 0과 1사이로 제한될테니, 우리는 로그 함수의 그래프에서 0과 1사이만 보면 된다.
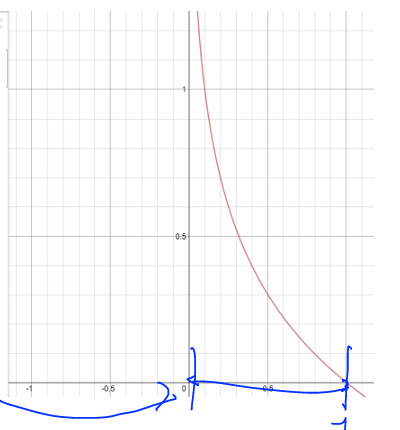
먼저, 정답이 $y = \begin{bmatrix}0 \ 1 \end{bmatrix}$ 인 경우에 각 결과 vector에 대한 비용함수 값을 비교해보자.
\[\hat{y} = \begin{bmatrix}0 \\ 1 \end{bmatrix} \rightarrow \begin{bmatrix}0 \\ 1 \end{bmatrix} \odot (-\log{(\begin{bmatrix}0 \\ 1 \end{bmatrix})}) = \begin{bmatrix}0 \\ 1 \end{bmatrix} \odot ((\begin{bmatrix}-\log{0} \\ -\log{1} \end{bmatrix})) = \begin{bmatrix}0 \\ 1 \end{bmatrix} \odot \begin{bmatrix}\infty \\ 0 \end{bmatrix} = \begin{bmatrix}0 \\ 0 \end{bmatrix} \Rightarrow 0\] \[\hat{y} = \begin{bmatrix}1 \\ 0 \end{bmatrix} \rightarrow \begin{bmatrix}0 \\ 1 \end{bmatrix} \odot (-\log{(\begin{bmatrix}1 \\ 0 \end{bmatrix})}) = \begin{bmatrix}0 \\ 1 \end{bmatrix} \odot ((\begin{bmatrix}-\log{1} \\ -\log{0} \end{bmatrix})) = \begin{bmatrix}0 \\ 1 \end{bmatrix} \odot \begin{bmatrix}0 \\ \infty \end{bmatrix} = \begin{bmatrix}0 \\ \infty \end{bmatrix} \Rightarrow \infty\]다음으로 정답이 $y = \begin{bmatrix}1 \ 0 \end{bmatrix}$ 인 경우를 비교해보자.
\[\hat{y} = \begin{bmatrix}1 \\ 0 \end{bmatrix} \rightarrow \begin{bmatrix}1 \\ 0 \end{bmatrix} \odot \begin{bmatrix}0 \\ \infty \end{bmatrix} = \begin{bmatrix}0 \\ 0 \end{bmatrix} \Rightarrow 0\] \[\hat{y} = \begin{bmatrix}0 \\ 1 \end{bmatrix} \rightarrow \begin{bmatrix}1 \\ 0 \end{bmatrix} \odot \begin{bmatrix}\infty \\ 0 \end{bmatrix} = \begin{bmatrix} \infty \\ 0 \end{bmatrix} \Rightarrow \infty\]두 경우 모두 결과와 예측이 동일할 떄는 비용함수의 값이 작고, 다를 때는 큰 것을 확인할 수 있다. 따라서 cross-entropy 식을 비용함수로 사용하는 것은 적절해 보인다.
cf. 로지스틱 회귀 비용함수 vs cross-entropy
로지스틱 회귀의 비용함수와 cross-entropy는 본질적으로 같다. 앞서 softmax 함수를 적용한 이후에 원-핫 인코딩으로 가장 큰 요소를 1, 나머지를 0으로 만든다고 했다. 로지스틱 화귀의 비용함수의 $\hat{y}$ 에 이를 반영하면 cross-entropy 식이 도출된다.
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기