비용 함수
로지스틱 회귀에서 비용함수는 다음과 같이 정의한다.
\[cost(h_{\theta}, y) = -y \log{(h_{\theta}(x))} - (1 - y) \log{(1-h_{\theta}(x))}\]식을 이해해보자.
먼저, 정답이 1인 경우(y=1)를 생각해보자. 비용함수의 식은 $-\log{(h_{\theta}(x))}$ 가 된다. 즉, 가설함수의 값이 1에 가까울 수록 함수의 결과 값이 0에 가까워진다. 반대로, y=0인 경우애는 비용함수가 $-\log{(1-h_{\theta}(x))}$ 이며, 가설함수의 값이 0에 가까울수록 비용이 줄어드는 형태가 된다.
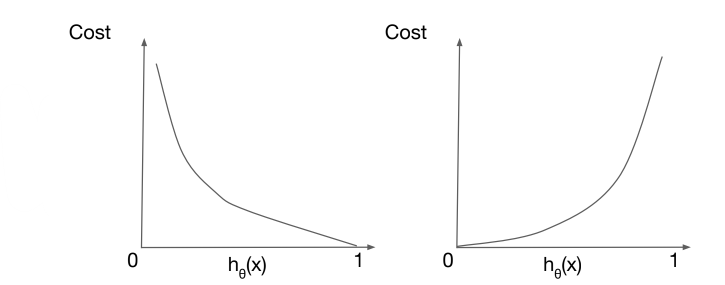
비용함수를 최소화하는 방법은 경사하강법을 사용하면 된다.
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기