경사 하강법
지난 시간에 배운 가설 식에서 b를 제거하여 단순화를 하고 시작하자.
\[H(x) = Wx\] \[\displaystyle cost(W) = \frac{1}{m} \sum_{i=1}^{m}{(Wx_i - y_i)^2}\]W 값에 따른 비용함수의 변화를 그래프로 표현하면 다음과 같아질 것이다.
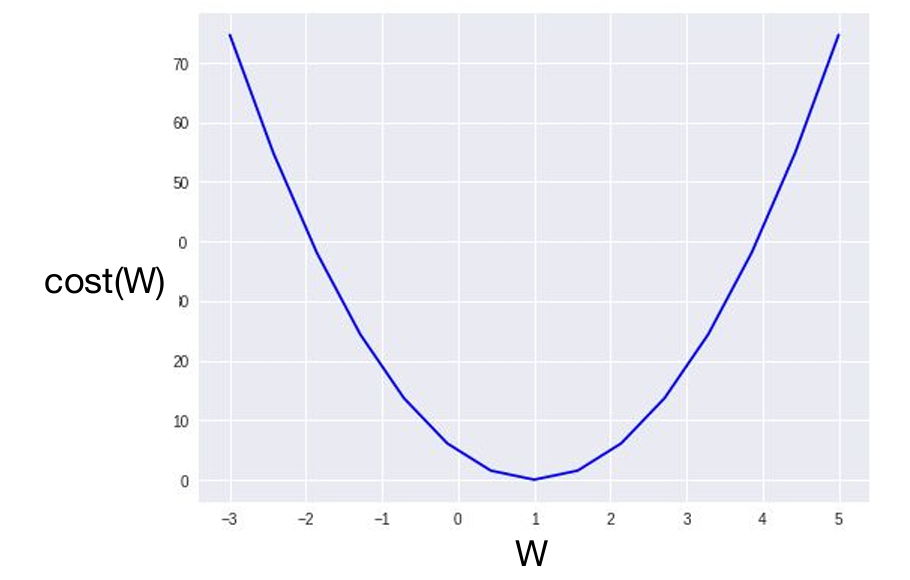
우리가 찾고자 하는 것은 위 그래프의 최소점이다. 따라서 그래프 위 임의의 한 점에서 시작헸을 때, 아래 그림과 같이 학습이 진행되어야 한다.
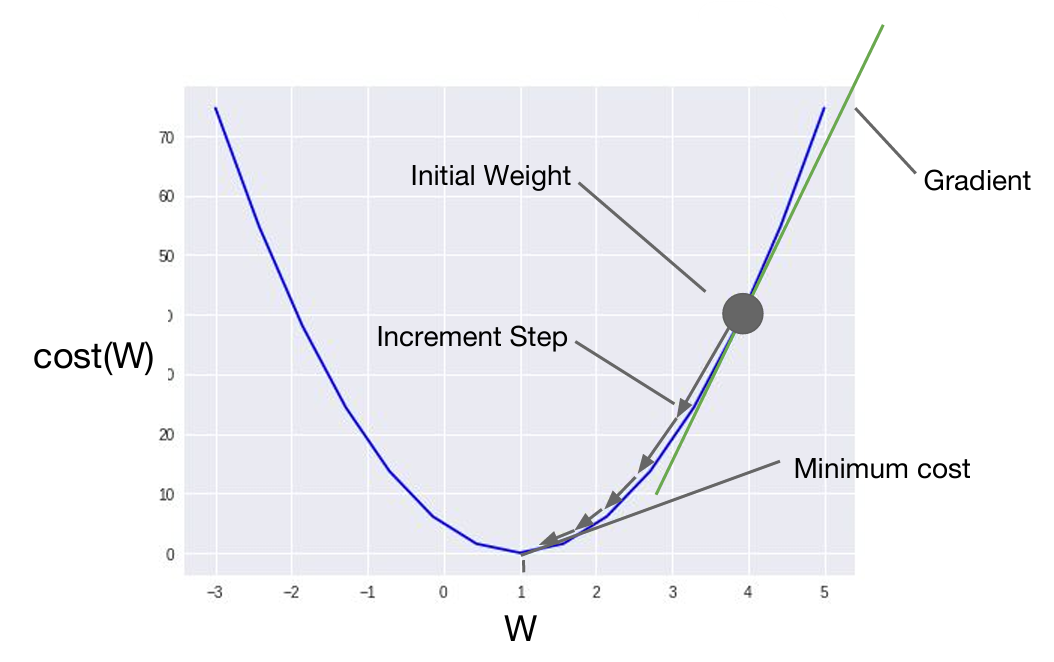
그래프 위 미분계수(경사)에 따라 W값이 커져야 하는지, 작아져야 하는지를 알 수 있다. 따라서 W 값의 업데이트는 다음과 같이 할 수 있다.
\[\displaystyle W := W - \alpha \frac{\partial}{\partial W} \frac{1}{2m} \sum_{i=1}^{m}{(W(x_i)-y_i)^2}\]분모에 $m$ 대신 $2m$으로 표기한 것은 편미분 과정에서 식을 좀 더 간단하게 만들기 위해서이다.
$\alpha$ 는 학습률로, W 값을 한 번에 얼마나 많이 업데이트 할 것인지를 결정한다. 학습률이 크면 최적에 빠르게 수렴할 것이고, 작으면 천천히 수렴할 것이다.
위 식을 정리하면 최종적으로 다음과 같이 정리할 수 있다.
\[\displaystyle W := W - \alpha \frac{\partial}{\partial W} \frac{1}{m} \sum_{i=1}^{m}{(W(x_i)-y_i)x_i}\]믈론 비용함수의 그래프가 예쁘지 않아서, 경사하강법을 사용하더라도 전역 최적에 수렴하지 못할 수도 있다.
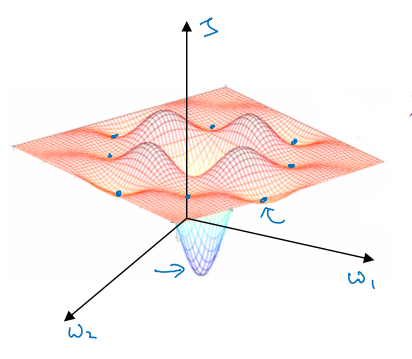
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기