About this Article
- Authors: Minseok Choi, Dohyun Lee, Jaegul Choo, Daniel Rim
- Journal: arXiv preprint
- Year: 2024
- Official Citation: Choi, M., Lee, D., Choo, J., & Rim, D. (2024). OPT-OUT: Investigating Entity-Level Unlearning for Large Language Models via Optimal Transport. arXiv preprint arXiv:2406.12329.
Accomplishments
- Developed a new unlearning technique (OPT-OUT), a technique that removes a certain entity’s data without seriously harming model’s performance.
Key Points
1. Basic Concepts
Machine unlearning(MU) is the task of reversing the learning process to make a model forget the influence of data. As the privacy issue is rising, MU is becoming an important technique. However, it is almost impossible to select and modify specific parameters according to the information to remove. Therefore, many alternatives approaches are being researched. In this research, authors introduced two main accomplishments.
- Entity-Level Unlearning Dataset (ELUDe)
- OPT-OUT
2. Entity-Level Unlearning Dataset (ELUDe)
Entity-Level Unlearning Dataset (ELUDe) is a dataset consisting of 20 real-world entities in Wikipedia pages. ELUDe is used for simulating real-world unlearning scenarios, such as removing a certain user’s profile and memory in LLM service. In specific, ELUDe consists of as follows.
- Real-world entities (20): Selected from the most popular Wikipedia pages. By using popular pages, the data is likely already memorized by the LLM, reducing the need for additional fine-tuning before unlearning can be evaluated.
- Neighboring entities (10 for each, total 144 with overlap): Selected by mining neighboring pages of above 20 entities.
- QA pairs: Each Wikipedia pages are transformed into QA pairs. Instead of inputing entire original pages into LLM, QA pairs can prevent omitting specific information during training. It is also easy to test whether the model actually forget the information.
3. Methodology
1. Notations
- $x={x}_{i=1}^{T}$: A token sequence.
- $\mathcal{D} = {\mathrm{x}}_{i=1}^N$: A training dataset with a token sequence.
- $\mathcal{D}_f$: A forget set, a specific subset of data to remove.
- $\mathcal{D}_r$: A retain set, a specific subset of data to be retained.
- $\mathcal{D}_f^t$: A proxy forget set for entity 1. As it is impossible to accurately erase all knowledge associated with a target entity by identifying and deleting a specific subset, authors (and many researchers) use a proxy forget set.
- $\mathcal{D}_r^t$: A proxy retain set for entity 1.
- $\phi_{\theta}$: A model to train.
2. Entity-Level Unlearning
The goal of entity-level unlearning is to update a model $\phi_{\theta}$ to $\phi_{\theta^{\prime}}=S(\phi_{\theta};\triangledown_{f}^{t})$, where S is an unlearning function. S ensures that the performance of model is preserved after removing $\emptyset_{f}^{r}$.
3. Knowledge Unlearning
The most simple and conceptually idealistic way is to use gradient ascent for the forget set. This can intentionally maximize the loss of the forget set and make it harder to predict the next token. The following is the formula, only negative sign is added in the front of gradient descent.
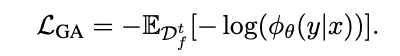
However, some researches revealed that using gradient ascent is catastrophic. Therefore authors used an improved version, which is called Negative Preference Optimization(NPO):
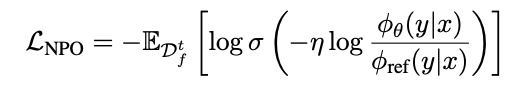
- $\sigma$: the sigmoid function
- $\eta(>0)$: an inverse of temperature. Higher will make the model definitely avoid unfavorable answers.
- $\phi_{ref}$: a reference model. Authors also explicitly trained with a retain set.
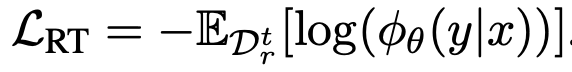
4. OPT-OUT with Wasserstein regularization
OPT-OUT is a fine-grained unlearning approach grounded in optimal transport theory. One of the optimal transport theories is the Wasserstein distance and authors used it in the way of the Wasserstein regularization.
- The Wasserstein distance (Earth Mover’s Distance): Address optimal transport problem by measuring the minimum effort required to move one distribution of mass to another.
Authors thought that the Wasserstein distance can estimate the optimal transportation cost between parameters. A theoretical optimal solution $\pi^{*}$ of the Wasserstein distance is as follows.
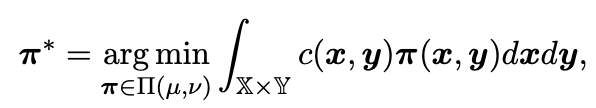
- $\mu$: a source distribution, sampled from probability space $\mathbb{X}\in\Omega$
- $\eta$: a target distribution, sampled from probability space $\mathbb{Y}\in\Omega$
- $\pi \in \mathcal{P}(\mathbb{X} \times \mathbb{Y})$: a probabilistic coupling, in other words, all possible solutions.
- $c(x,y)$: a cost function that quantifies the movement of x to y.
The above formula is changed into discrete version.
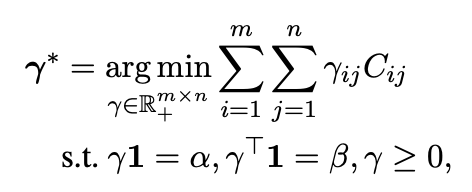
- $\gamma^{*}$: an optimal solution.
- $C \in \mathbb{R}_+^{m \times n}$: a cost matrix, defining the cost to move mass from bin $\alpha_{t}$ to bin $\beta_{j}$.
- $\alpha, \beta$: histograms on the simplex that represents the weights of each sample in the source and target distributions. Based on the equations, the Wasserstein distance between initial weight $\theta_{0}$ and finite p-moments parameters is computed as a below.
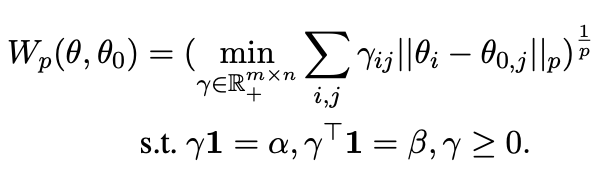
However, due to too high time and space complexity, the Sliced Wasserstein Distance (SWD), which is an approximate version, is used instead. SWD reduced the complexity by projecting the distributions onto random slices and computed the distance in lower dimensions. Monte Carlo approximation of p-sliced Wasserstein distance is given by
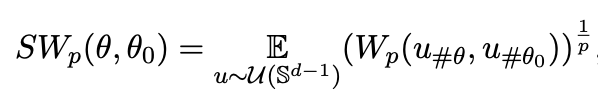
- $\mathcal{U}(\mathbb{S}^{d-1})$: uniform distribution on the unit sphere $\mathbb{R}^{d}$
- u_{#\theta}, u_{#\theta_{0}}: pushforwards(move the distribution by pushing) of the projections of and $\theta_{0}$ along the direction of $u \in \mathbb{S}^{d-1}$.
5. Overall Loss
The final loss is as a following equation.
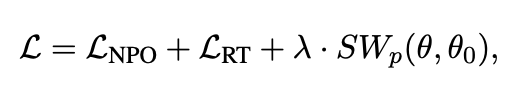
4. Evaluation Metrics
Authors used three metrics and two overall scores.
- Three metrics (For all three metrics, lower value is good for the forget set.)
- Probability: Model’s confidence about the answer.
- ROUGE: The similarity between the generated answer and the ground truth.
- Truth Ratio: Investigation whether the model can distinguish slightly modified (wrong) answer.
- By combining the three metrics, two overall scores are generated.
- Forget Quality(FQ): a harmonic mean of three metrics on the forget set. Higher value means forgetting is working well.
- Retain Quality(RQ): a harmonic mean of six metrics, three from the retain set, and the other three from the world set. Higher value means memorizing performance is good. The world set is an independent set from the forget and retain, to check the common sense of the model.
Figures & Table Explanation
1. Unlearning performance of OPT-OUT (Table 1)
Rows are unlearning methods, and columns are benchmarks. The experiment was performed on two different datasets. (Guardrail is not an actual unlearning method, it is just about prompting.) FQ (Forget Quality) reflects the harmonic mean of ground-truth token probabilities, ROUGE-L recall scores, and truth ratio over the forget set, while RQ (Retain Quality) is computed across the retain and world sets. Methods are also assessed on eight LLM benchmarks to evaluate the retention of overall model capabilities.
2. Results of Membership Inference Attacks (MIA) experiment (Table 2)
Membership Inference Attacks(MIA) is an attack that attackers try to distinguish whether a certain entity was a member of dataset. If attackers successfully determine the fact, a personal information could be leaked. Authors trained a binary classifier that does MIA. If the accuracy of the classifier is 50%, it is similar to a random classifier, and it means that unlearning was successful. Almost all unlearning method had a good MIA resistance.
3. Results of Adversarial Prompt Attacks experiment (Fig. 3)
Adversarial Prompt Attacks is an attack that attackers use malicious prompts to bypass a safeguard and achieve a personal information. OPT-OUT was good at preventing adversarial prompt attacks.
4. The effect of Wasserstein Distance (Table 3)
Other regularization methods was not good at unlearning (Manhattan) or preserving the performance (Euclidian and Cosine). However, Wasserstein distance showed the best overall results.
5. The effect of neighboring data augmentation (Fig. 4)
Without neighboring data augmentation, the model had a hard time differentiating forget and retain examples.
Limitations & Possibility for Further Research
- Wikipedia entities are slightly different from actual users. Further work can be extended to real-world data and users.
-
Susceptible to generating gibberish(impossible to understand) post-learning. After unlearning, the method that author used was susceptible to generating gibberish. Combining with IDK(I Don’t Know, answering I don’t know instead of gibberish) method or remapping outputs could solve this.
- Unable to test at large scale model. More exploration for unlearning techniques is needed.

댓글남기기