분류 문제
지금까지 살펴본 회귀 문제는 특정 값을 예측하는 것이었다. 지금부터 살펴볼 문제는 특정 데이터가 어느 집단에 속할지를 결정하는 분류(classification) 문제이다. 예시로 다음과 같이 경계선을 긋는 문제를 들 수 있다.
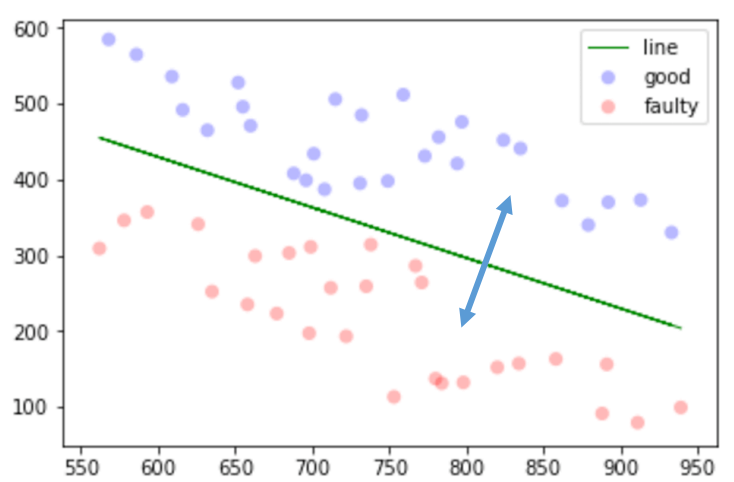
분류 문제를 해결하는 아이디어는 집단에 속할 확률을 구하는 것이다. 물론 선형 회귀를 이용해서 풀 수 있으나, 다음과 같은 문제점들을 해결해야 한다.
- 1 이상 또는 0이하의 수들이 나올 수 있음.
- 1 또는 0으로 정확히 표현이 힘듦.
- 변수가 y에 영향을 주는 정도가 꼭 비례하지는 않음.
- 확률로 표현해야 함.
위 문제점들을 해결하기 위해 보통 로지스틱 회귀를 사용한다.
로지스틱 회귀
어떤 사건이 일어날 확률을 $P(X)$, 일어나지 않을 확률을 $1 - P(X)$ 라고 할 때, 오즈비(Odds Ratio)는 다음과 같이 계산한다.
\[\frac{P(X)}{1-P(X)}\]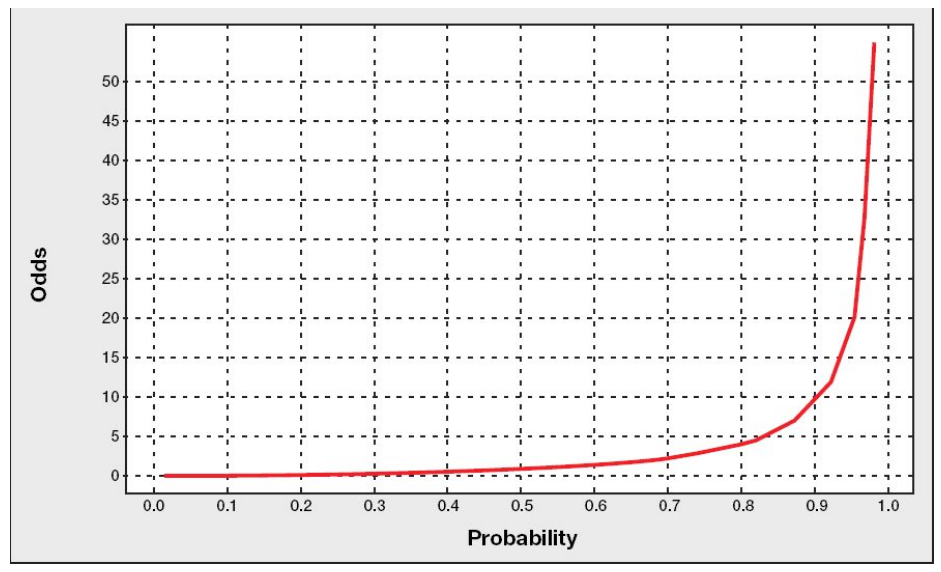
위 같은 오즈비는 범위가 0과 무한대($\infty$) 사이에 한정되고, 대칭성이 없다는 단점이 있다. 이는 오즈비에 로그를 붙여 해결(로짓함수, Logit Function)할 수 있다.
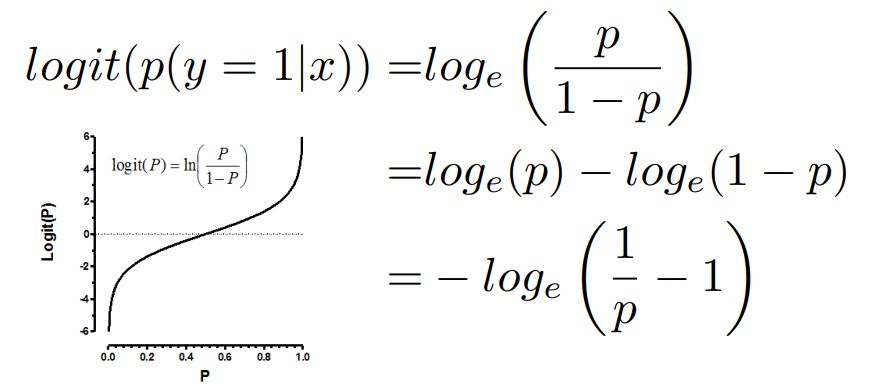
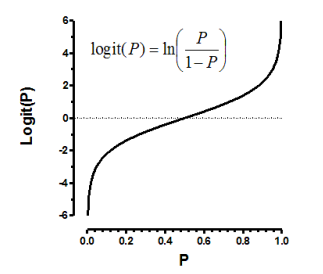
우리가 원하는 것은 확률을 구하는 것이기 때문에 역함수를 취해준다.
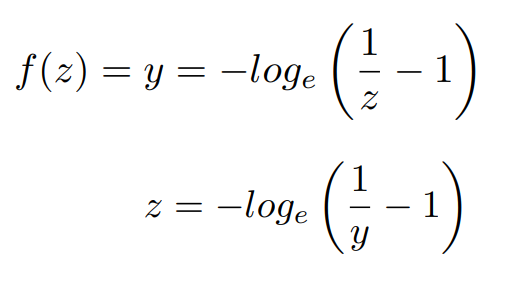
이제 y에 관해 정리한다.
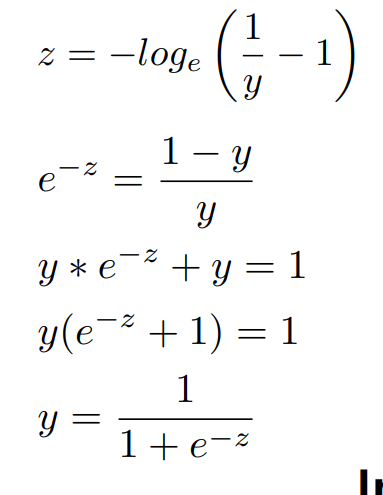
이렇게 구해진 함수가 시그모이드 함수(Sigmoid Function)이다.
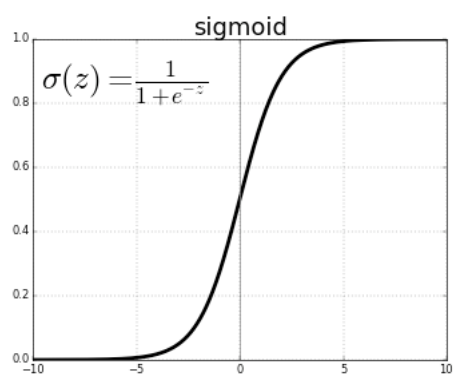
보통 시그모이드 함수의 값이 0.5보다 크면 집단에 속하는 것으로(1), 그렇지 않으면 속하지 않는 것(0)으로 분류한다.
로지스틱 회귀 학습
로지스틱 회귀에서는 비용은 다음과 같이 정의된다($h_{\theta}(x)$ 는 시그모이드 함수).
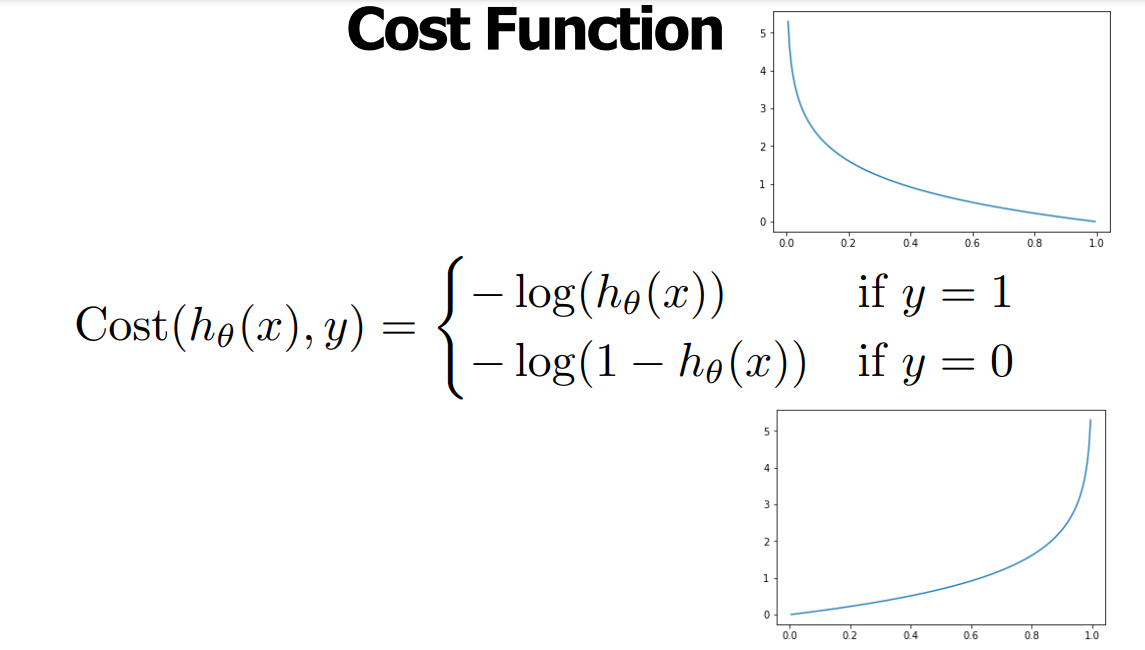
이렇게 정한 것에는 나름의 이유가 있다. 비용은 당연히 작을수록 좋은 것이기 때문에, 위 그림에 있는 그래프의 모양을 고려한다면 그 이유를 납득할 수 있다.
경사하강법을 적용하기 위해서는 미분을 해야 한다. 일단 비용 함수는 다음과 같다.
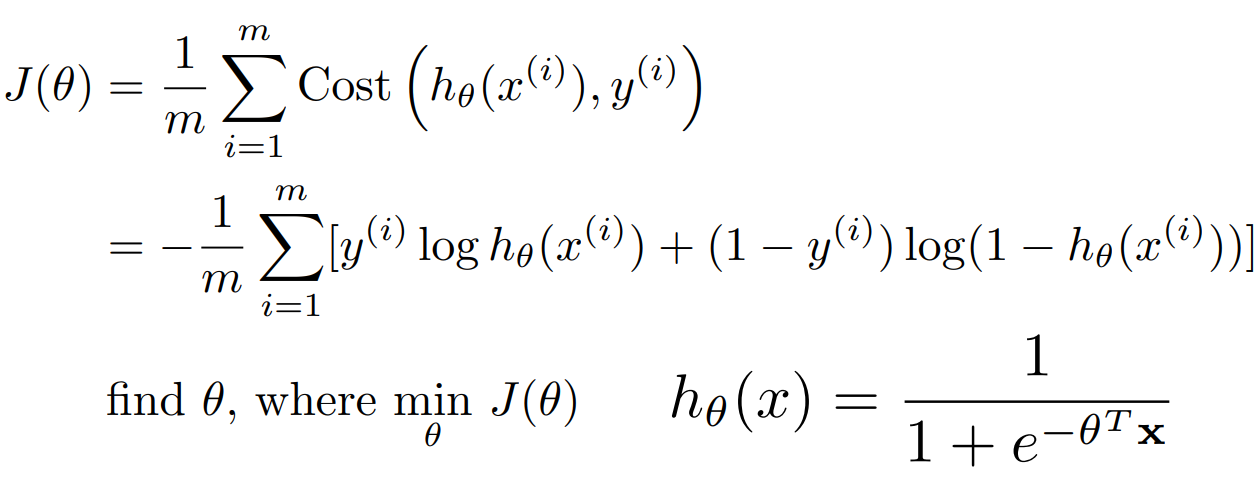
이제 식을 조금 정리해보자.
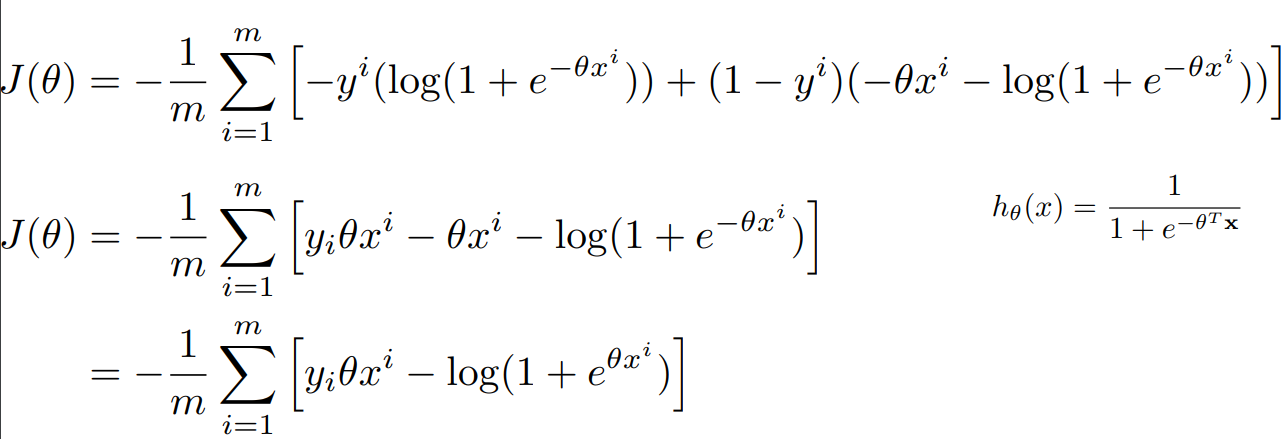
이를 $\theta$ 에 대해 미분한다. 먼저 첫째 항부터 미분한다.
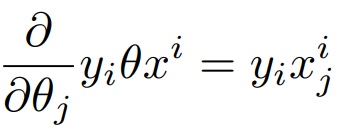
다음은 둘째 항의 미분 과정이다.
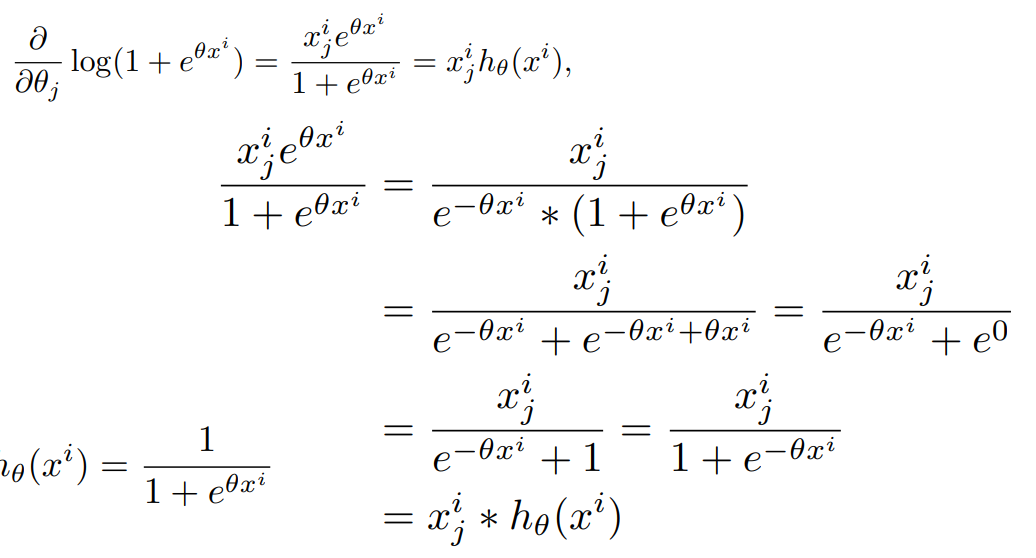
이제 위 두 개를 합해서 최종 미분 식을 구한다.
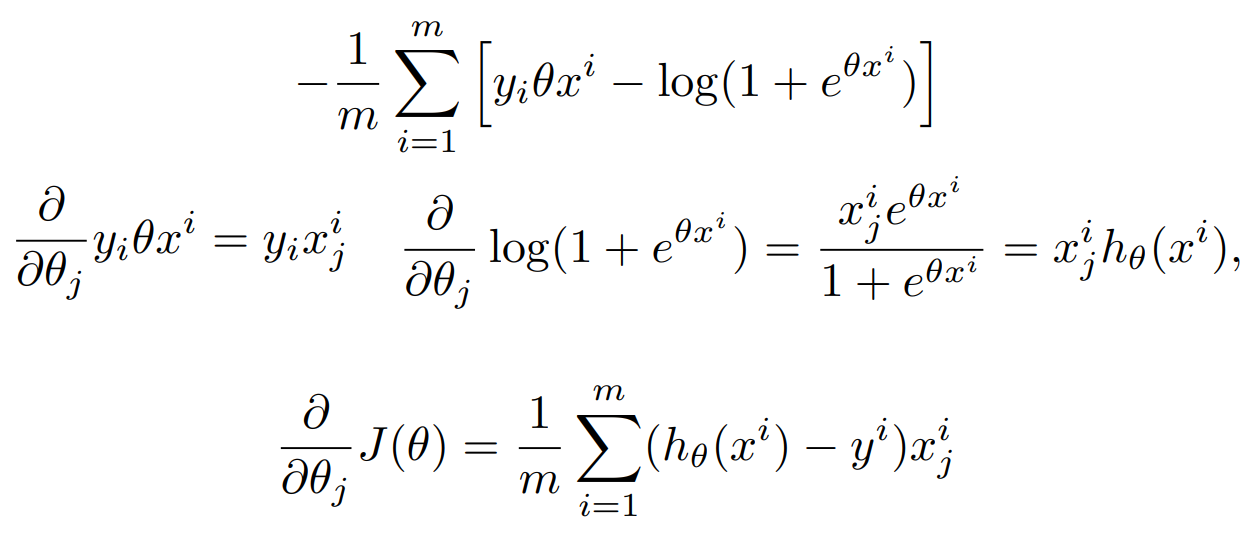
미분이 끝났으면 가중치 업데이트를 해야 한다.
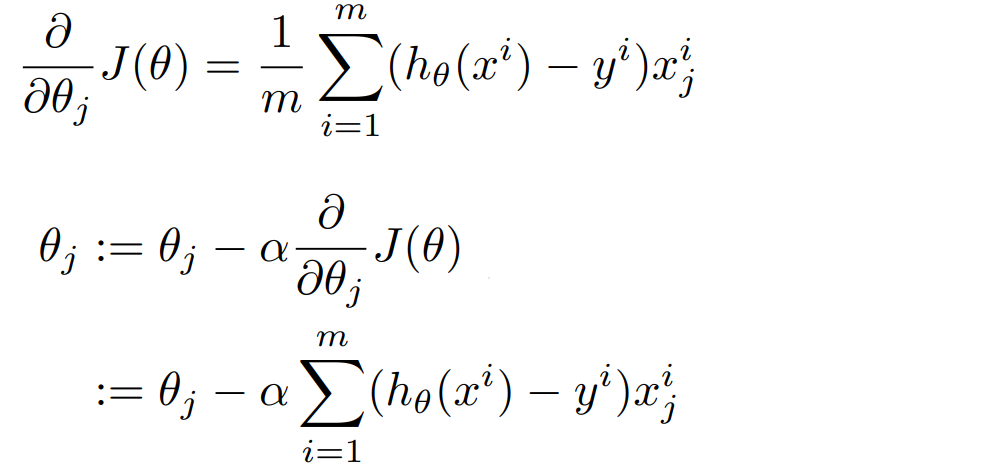
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기