배치 경사하강법
보통 경사하강법이라고 하면 한 번에 모든 데이터에 대해 경사하강법을 시행해서 이를 평균 내는 ‘배치 경사하강법(Full-batch Gradient Descent)’을 의미하는 경우가 많다.
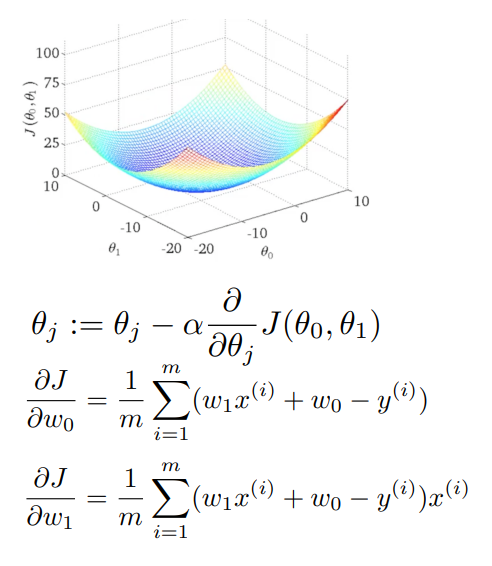
배치 경사하강법은 다음과 같은 특징이 있다.
- 업데이트 횟수가 감소해서 계산상 효율(속도)이 증가한다.
- 안정적인 비용 함수 수렴이 가능하다.
- 지역 최적화가 가능하다.
- 메모리가 더 필요하다는 문제점이 있다.
- 대규모 데이터셋의 경우 모델과 매개변수의 업데이트가 느려진다.
확률적 경사하강법
확률적 경사하강법(Stochastic Gradient Descent, SGD)은 전체 데이터셋에서 하나의 데이터를 랜덤하게 뽑아서 이를 train set으로 이용하는 방식을 말한다. 데이터를 넣기 전에 섞는 과정이 포함되어야 한다.
확률적 경사하강법의 특징은 다음과 같다.
- 모델 업데이트를 빈번하게 하면서 모델의 성능과 개선 속도를 확인할 수 있다.
- 일부 문제에 대해서 더 빠르게 수렴한다.
- 지역 최적화를 회피하는 것이 가능하다.
- 대용량 데이터 시 시간이 오래 걸린다.
- 더 이상 비용 함수의 값이 줄어들지 않는 시점의 관찰이 어렵다.
미니배치 경사하강법
미니배치 경사하강법(Mini-batch Gradient Descent)은 전체 데이터를 미니배치라고 하는 작은 집단으로 나누어 학습하는 방법이다. 배치 경사하강법과 확률적 경사하강법의 절충안이며, 일반적으로 가장 많이 쓰인다.
배치의 크기(Batch-size)는 한 번에 학습되는 데이터의 개수를, epoch는 전체 데이터를 몇 번 학습하는지를 의미한다. 예를 들어, 총 5120개의 데이터가 있고, 배치의 크기가 512라면 10번을 학습해야 1epoch가 되는 셈이다.

위 의사코드에서 마지막 줄의 시그마를 눈여겨 보자. i가 증가함에 따라 전체 데이터에서 구간이 설정되는 것, 즉 미니배치가 생성되는 것을 표현한 것이다.
경사하강법 간 비교
for epoch in range(epochs):
X_copy = np.copy(X)
if is_SGD: # 1
np.randon.shuffle(X_copy)
batch = len(X_copy) // batch_size
for batch_count in range(batch): # 2
X_batch = np.copy(
X_copy[batch_count * batch_size : (batch_count + 1) * batch_size]
)
위 코드만 있으면 배치 경사하강법, 확률적 경사하강법, 미니배치 경사하강법 모두 구현이 가능하다. 일단 # 1에서 확률적 경사하강법에 필요한 단계인 랜덤 셔플을 구현한다. 그리고 # 2에서 미니배치를 구현한다. 만약 미니배치를 나누지 않는 경사하강법이라면 batch_size가 1일 것이다.
다음 코드는 각 경사하강법의 특징을 잘 보여준다. 실제로 작동도 한다!
gd_lr = linear_model.LinearRegressionGD(eta0 = 0.001, epochs = 10000, batch_size=1, shuffle=False)
bgd_lr = linear_model.LinearRegressionGD(eta0 = 0.001, epochs = 10000, batch_size=len(X), shuffle=False)
sgd_lr = linear_model.LinearRegressionGD(eta0 = 0.001, epochs = 10000, batch_size=1, shuffle=True)
msgd_lr = linear_model.LinearRegressionGD(eta0 = 0.001, epochs = 10000, batch_size=100, shuffle=True)
수렴하는 과정을 그래프로 비교하면 다음과 같다.
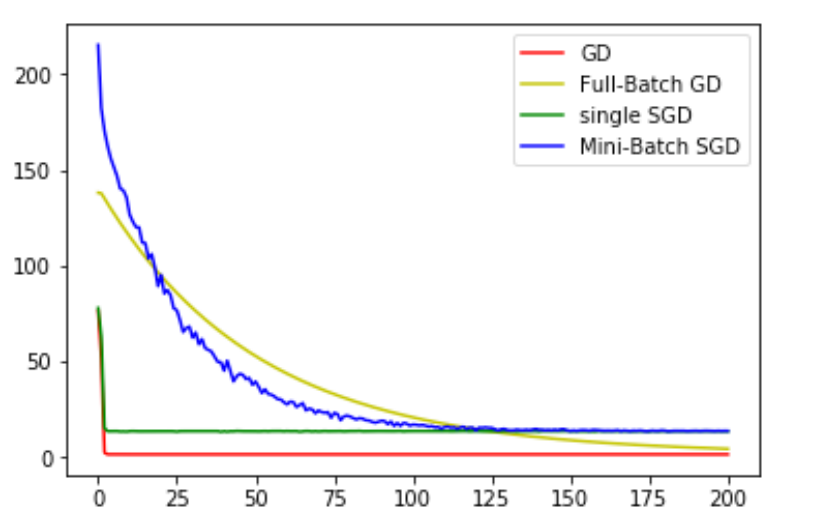
그래프에서 안정적으로 감소하는 두 방식은 일반 경사하강법과 배치 경사하강법이다. 반면에 확률적 과정이 포함되는 확률적 경사하강법, 미니배치 경사하강법은 진동이 많은 것을 볼 수 있다.
학습률 감소
일정한 주기로 학습률을 감소시킨다면 비용 함수를 더 확실하게 수렴시킬 수 있을 것이다. 특정 epoch마다 주기적으로 학습률을 감소시킬 수 있으며, 지수 감소와 1/t 감소의 방법이 있다.
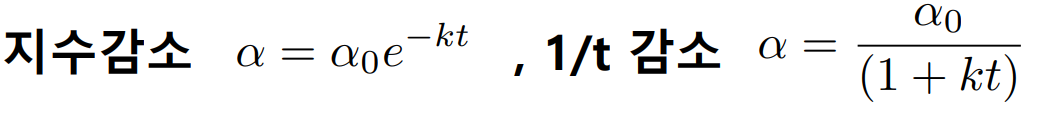
하지만 학습률 감소는 또다른 초매개변수를 설정해주어야 한다는 단점이 있다.
종료조건 설정
확률적 경사하강법에서 더 이상 비용 함수의 값이 줄어들지 않는다면 학습을 중단시킬 수 있다. 성능이 더는 좋아지지 않으므로 필요 없는 연산을 방지하는 것이다. 종료 조건(tol > loss - previous_loss)을 설정하면 되는데, 이는 또다른 초매개변수이다.
과대적합과 규제
머신러닝에서는 편향-분산 트레이드 오프가 존재한다. 편향(Bias)은 잘못된 데이터로 학습하여 원래 모델에서 많이 멀어질 경우(잘못된 매개변수만 업데이트) 증가한다. 분산(Variance)은 모든 데이터에 민감하게 학습해서 결국 모델이 하나도 제대로 설명하지 못하는 경우에 증가한다.
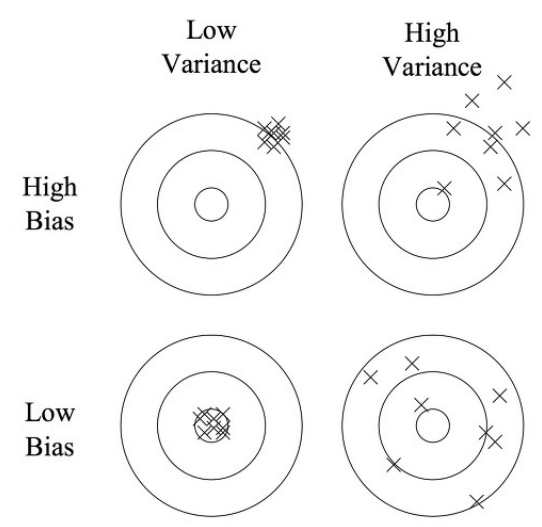
위 그림은 화살의 과녁판으로 편향과 분산을 설명한 것이다. 편향만 큰 경우는 화살들이 모여있기는 하지만 우리가 원하는 중심부에서 멀어져 있다. 분산만 큰 경우는 화살들이 흩어져 있다. 왼쪽 위의 경우 과소적합(Underfitting)이고, 오른쪽 아래의 경우 과대적합(Overfitting)이다.
과대적합을 줄이는 방법으로는 더 많은 데이터를 이용하거나 매개변수를 줄이는 방법이 있다. 또다른 방법으로는 규제(Regularization)가 있다.
규제의 기본적인 아이디어는 비용 함수에 매개변수에 대한 페널티 항을 추가해서, 매개변수의 변동에 따라 비용 함수의 변동이 심하도록 하는 것이다. 그렇게 하면 모델이 학습하는 과정에서 매개변수를 크게 변화시키기 힘들 것이다.
규제의 종류에는 L2 규제와 L1 규제가 있다.
L2 규제는 유클리디안 거리 항을 추가한다. 주의해야할 사항으로는 절편 값에 대해서는 페널티 항을 부여하지 않는다.
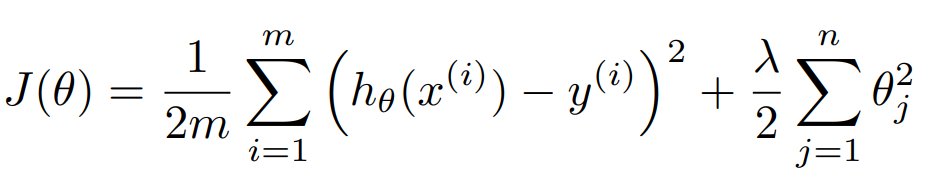
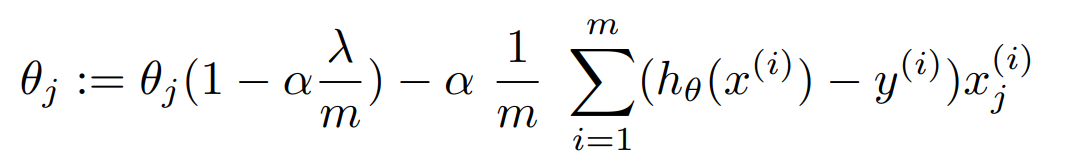
L1 규제는 맨해튼 거리 항을 추가한다.
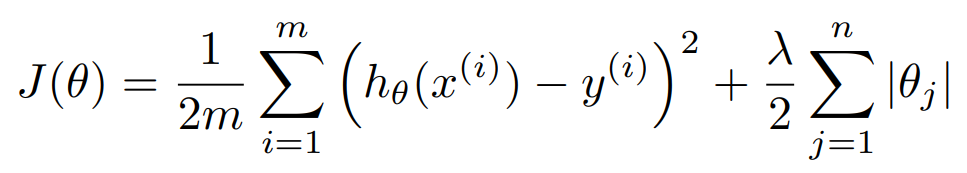
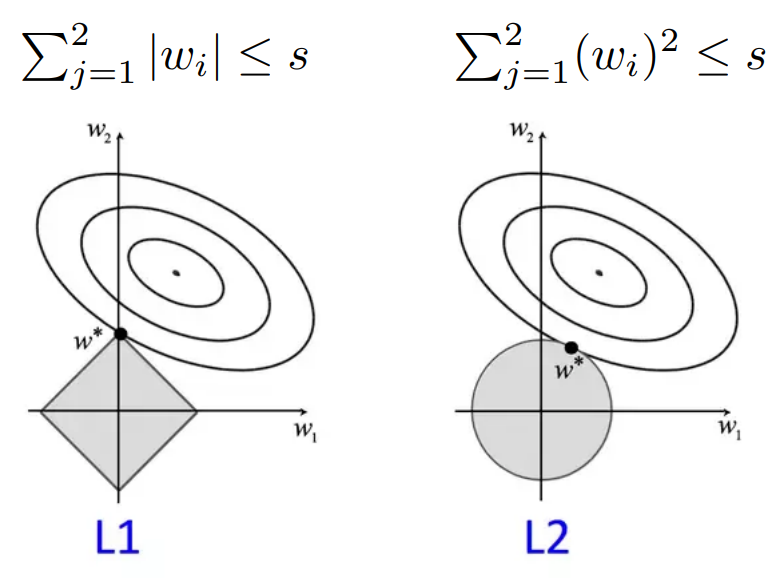
각 규제를 그래프로 나타내면 위와 같다. 타원형의 그래프는 기본적인 비용함수를 의미한다. 왼쪽 그래프는 L1 규제, 오른쪽 그래프는 L2 규제이다. 기존 비용함수 그래프와 규제 그래프의 접점에서 매개변수가 결정된다.
L2 규제는 미분 과정에 절댓값이 없기 때문에 안정적으로 답을 얻을 수 있고, 한 가지 답만 얻을 수 있다.
L1 규제의 경우, 접점에서 한 매개변수가 0인 것을 볼 수 있다. 이처럼 L1 규제를 사용하면 중요도가 낮은 매개변수를 거를 수 있다는 장점이 있다. 다만 L2 규제와는 다르게 미분이 좀 어렵다는 특징이 있다.
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기