경사 하강법
경사 하강법은 미분을 이용해 최적값을 찾는 과정이다. $f(x) = x^2$ 의 그래프가 있을 때, 최솟값은 극솟값을 가지는 $x=0$ 일 가능성이 높다. 만약 그래프 위 임의의 한 점에서 출발해서 극솟값을 가지는 $x=0$ 까지 도달하기 위해서는 경사를 따라 내려올 필요가 있다 (그래서 경사 하강법이라고 부른다).
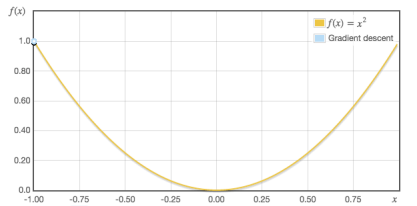
따라서 임의의 한 점에서 미분 계수를 구한 뒤, 이를 점차 갱신하는 방법으로 최적의 값을 찾는다.
\[x_{new} = x_{old} - \alpha \times 2x_{old}\]위 식에서 얼마나 빠른 속도로 갱신할지를 결정하는 $\alpha$ 를 학습률이라고 한다. 만약 학습률이 너무 낮다면 최적값을 찾는 시간이 오래 걸릴 것이고, 너무 높다면 최적값을 찾지 못하고 진동할 것이다.
또한, 한 가지 명심해야할 사실은, 지역 최적이 전역 최적이 아닐 수 있다는 사실이다.
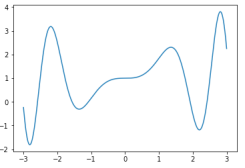
예를 들어, 위 그래프의 왼쪽에서 시작했을 때와 오른쪽에서 시작했을 때, 두 경우의 최적값이 다르다.
경사 하강법과 선형 회귀
우리가 경사 하강법을 통해 최적값을 찾아야 하는 함수는 비용 함수이다.
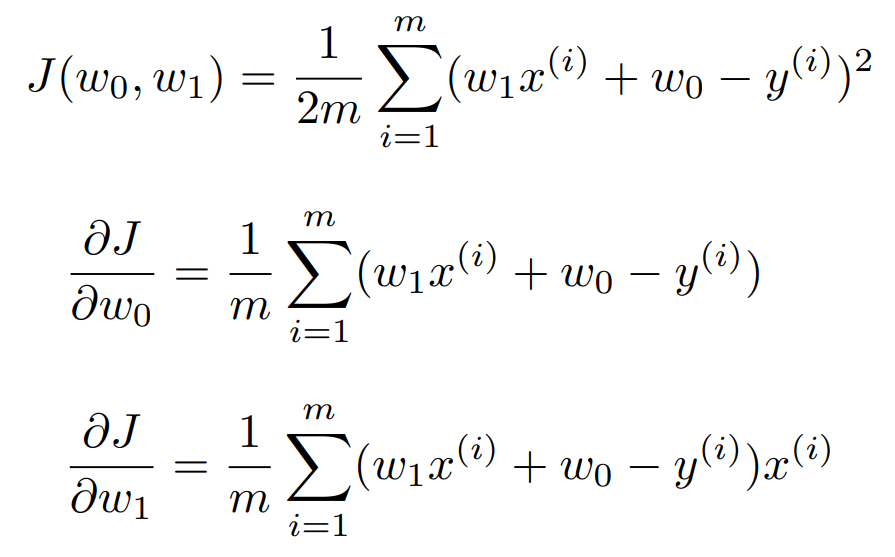
우리의 계획은 다음과 같다.
- $\theta_0$, $\theta_1$ 을 임의의 값으로 초기화.
- 비용 함수가 최소화 될 때까지 학습.
- 더 이상 비용 함수가 줄어들지 않거나 학습 횟수를 초과하면 종료.
이를 코드로 구현해보자. 일단 비용 함수와 가설 함수를 정의한다.
def hypothesis_function(X, theta):
return X.dot(theta)
h = hypothesis_function(X,w)
def cost_function(h, y):
return (1/(2*len(y))) * np.sum((h - y)**2)
이제 경사 하강법을 구현한다.
def gradient_descent(X, y, w, alpha, iterations):
theta = w # 1
m = len(y)
theta_list = [theta.tolist()] # 2
cost = cost_function(hypothesis_function(X, theta), y)
cost_list = [cost]
for i in range(iterations):
# 3
t0 = theta[0] - (alpha / m) * np.sum(
np.dot(X, theta) - y)
t1 = theta[1] - (alpha / m) * np.sum(
(np.dot(X, theta) - y) * X[:, 1])
theta = np.array([t0, t1]) # 4
if i % 10 == 0: # 과정을 보기 위한 추가 코드
theta_list.append(theta.tolist())
cost = cost_function(hypothesis_function(X, theta), y)
cost_list.append(cost)
return theta, theta_list, cost_list
부분별로 나누어서 자세히 알아보자.
일단 가장 먼저 $\theta$ 와 데이터의 크기(m)을 변수로 정해준다 (# 1).
그리고 비용 함수의 계산 결과를 변수로 만든 뒤, 이를 리스트에 넣는다 (# 2).
그리고 가장 핵심인 반복을 시작한다. 반복에서는 $\theta_0$, $\theta_1$ 의 값을 업데이트 한다 (# 3). 등장하는 수식은 비용 함수의 편미분 결과를 그대로 옮긴 것이다.
다음으로 업데이트된 $\theta$ 를 다시 theta에 넣어 최신화를 한다 (# 4). 반복이 끝난 뒤에 $\theta$ 값들을 모아서 한 번에 최신화하는 이유는 한 번의 반복에는 동일한 단계의 $\theta$ 값을 사용해야 하기 때문이다 (상식적으로 n번째 단계에서 생성된 $\theta_0$ 를 n번째 단계의 $\theta_1$ 을 구하는 데 사용하는 것은 말이 안된다).
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기