해시 테이블 크기 조정
우리는 항상 $m = \Theta(n)$ 을 만족하기를 원한다. 만약 m이 너무 작다면 느리고, m이 너무 크다면 메모리 공간의 낭비가 심할 것이다.
적당한 테이블 크기를 위해서는 먼저 작은 상수(ex. 8)로 시작하는 것이 좋다. 그리고 테이블 크기 조정이 필요하다면 그 때 크기를 바꾸면 된다. 테이블의 크기를 바꾸는 것은 그리 단순하지만은 않다. 사실상 처음부터 테이블을 다시 만드는 것과 다름 없기 때문이다. 먼저 테이블 크기를 키운 뒤에, 새로운 해시 함수로 다시 해싱을 해주어야 한다. 이는 $O(n + m) = O(n)$ 의 시간이 걸린다.
그럼 늘릴 크기는 어떻게 지정할까? 먼저, m을 1만 늘리는 경우를 생각해볼 수 있다. 이렇게 되면, 우리는 새로운 항목을 추가할 때마다 테이블 크기를 늘리는 과정을 반복해야 한다. n번의 삽입의 경우 $O(1 + 2 + \dots + n) = O(n^2)$ 의 시간이 걸린다.
m을 2배로 늘리면 어떨까? n번의 삽입에 $O(1 + 2 + 4 + 8 + \dots + n) (\log{n} 개) = O(n)$ 만큼의 시간이 걸릴 것이다.
분할상환 분석
자취를 위해 방을 하나 빌렸다고 해보자. 그럼 보통 월세를 내게 될텐데, 월세를 한 번에 결제하는 것이 부담스럽다. 이 경우에는 마치 할부처럼 매일 조금씩 돈을 내는 방법을 제안할 수도 있을 것이다. 이와 같은 방식을 분할상환이라고 한다.
해시 테이블에서는 ‘분할상환 분석(Amoritized Analysis)’을 적용했을 때의 특징이 있다. k번의 연산 시간이 $\leq k \cdot T(n)$ 이면, T(n)의 분할상환 연산시간이 든다고 말한다. 평균적으로 T(n)의 시간이 드는 것이라고 이해도 좋을 것이다.
예를 들어, 해시 테이블에 데이터를 삽입하는 것은 O(1)의 분할상환 시간이 든다. k개를 삽입하는 데 O(k)의 시간이 들기 때문에, 이를 k로 나누면 $\Theta(1)$ 이 되는 것이다.
해시 테이블에서 데이터 삭제
데이터 삽입이 아니라 삭제에 대해서도 알아보자. 데이터가 줄어서 $n = \frac{m}{2}$ 가 되었을 때 테이블을 반으로 줄이면 어떻게 될까? 예를 들어 m = 16, n = 8 인 상황에서 m을 8로 줄이는 것이다. 당장은 문제가 없겠지만, 만약 데이터가 하나 추가된다면 우리는 다시 테이블을 2배로 늘려야 한다. 단 1개의 데이터 개수 차이로 인해 테이블이 2배가 되었다가 절반이 되었다가를 반복하는 것이다.
이를 방지하기 위해서 우리는 $n = \frac{m}{4}$ 가 되었을 때 비로소 해시 테이블을 반으로 줄이는 방법을 사용한다. 이렇게 하면 삽입과 삭제에 모두 O(1)의 분할상환 시간이 걸린다.
문자열 매칭 - 간단 알고리즘
앞서 문서 내에 우리가 찾고자 하는 단어가 있는지 여부를 판단하는 일, 즉 ‘문자열 매칭’에서도 해시 테이블을 사용할 수 있다고 했다.
간단한 알고리즘부터 생각해보자. 우리가 찾고자 하는 문자열이 s, 문서가 t일 때 다음과 같은 의사코드로 문자열 매칭을 할 수 있다.
for i in range(len(t) - len(s)):
s == t[i:i + len(s)]
정말 이해하기 쉽다. t의 가장 앞부터 s와 매칭해보고, 그 다음 한 칸을 옮겨서 또 매칭해보고. 이 과정을 반복하는 것이다.
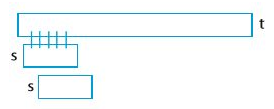
시간은 총 $O(\vert s \vert \cdot (\vert t \vert - \vert s \vert)) = O(\vert s \vert \cdot \vert t \vert)$ 만큼 걸린다. 즉, 잘못하면 2차의 무시무시한 시간이 걸리는 것이다!
문자열 매칭 - Karp-Rabin 알고리즘
본격적으로 좋은 알고리즘을 알아보기 전에, 롤링 해시를 비롯해 몇 가지 연산자를 알고 가자.
우리가 만약 어떤 문자열의 맨 앞 문자를 지우고, 맨 뒤에 문자 하나를 추가한다고 해보자. 이 상황에서 새로운 문자열의 해시 값을 구하는 매우 쉽다. 우리는 이미 기존 문자열의 해시 값을 가지고 있으므로, 겹치는 부분의 해시 값을 그대로 둔 뒤, 바뀌는 부분만 고려해서 계산하면 된다. 이를 롤링 해시(Rolling hash)라고 한다.
| 연산자 | 의미 |
|---|---|
| r() | 문자열 x의 합리적인 해시 함수 h(x) |
| r.append(c) | x를 보존하면서 문자열 x의 끝에 c를 넣는다. |
| r.skip(c) | 문자열 x의 첫 문자가 c라는 가정 하에 첫 문자를 지운다. |
롤링 해시를 응용하는 ‘Karp-Rabin 알고리즘’의 흐름을 이해해보자. 먼저, s와 ‘t 맨 앞의 s 길이’ 만큼의 해시 값을 비교한다. 그 다음에는 t에서 맨 앞 문자를 제거(skip)하고, 그 다음 문자를 추가(append)해서 롤링 해시를 구하면 된다. 새롭게 구한 해시 값이 s의 해시 값과 같은지 비교하면서 계속 반복하면 된다.
의사 코드로 살펴보자.
for c in s:
rs.append(c) # s에 c를 첨가한 뒤 롤링 해시 구하기
for c in t[:len(s)]:
rt.append(c) # t에 c를 첨가한 뒤 롤링 해시 구하기
if rs() == rt(): # 해시 값 비교
pass # 간단 알고리즘으로 진짜 같은 문자열인지 판단
for i in range(len(s), len(t)):
rt.skip(t[i-len(s)]) # 맨 앞 문자 제거
rt.append(t[i]) # 그 다음 문자 추가
if rs() == rt(): # 해시 값 비교
pass # 간단 알고리즘으로 진짜 같은 문자열인지 판단
해시 값이 다른 경우는 말할 필요도 없이 다른 문자열이다. 그러나 해시 값이 같다면? (위 의사코드에서 pass라고 구현된 부분) 해시 값이 같다고 무조건 같은 문자열은 아니다. 이 때는 앞서 살펴본 간단 알고리즘으로 진짜 같은 문자열인지를 판단해주면 된다.
Karp-Rabin 알고리즘의 기대 시간은 ‘$O(\vert s \vert + \vert t \vert + $ # matches $ - \vert s \vert)$’ 만큼 걸린다.
상수 시간만 사용하는 해시 함수
문자열 x를 a진법으로 쓰여진 여러 자리의 수 u로 볼 때, 지난 시간에 배운 나머지 연산법은 연산당 상수 시간만 사용하는 해시 함수이다.
다음은 append와 skip을 나머지 연산법에 적용한 것이다.
r() = u mod p (p는 $\geq \vert s \vert$ 인 무작위의 소수)
r.append(c): (u $\cdot$ a + ord(c)) mod p = [(u mod p) $\cdot$ a + ord(c)] mod p
r.skip(c): [u - ord(c) $\cdot$ ($a^{\vert u \vert - 1}$ mod p)] mod p = [(u mod p) - ord(c) $\cdot$ ($a^{\vert x - 1 \vert}$ mod p)] mod p
ord(c) 는 c를 숫자로 바꾸어주는 파이썬 연산자이다.
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기