하한선
탐색과 정렬에 대해 최저 소요 시간(하한선)은 다음과 같다.
- n개의 전처리된 요소 탐색: $\Omega(\log{n})$
- n개의 요소 정렬: $\Omega(n\log{n})$
비교 모델
계산에서의 비교 모델은 n개의 알 수 없는 요소들(black boxes)이 입력으로 들어왔을 때, 다른 연산 대신 비교($<, \, >, \, \leq, \, \geq, \, =$)만을 하는 모델을 말한다. 걸리는 시간은 비교의 개수와 동일하다.
비교 모델은 결정 트리로 나타낼 수 있다. 결정 트리에는 모든 가능한 비교와 그 결과가 있다. 이진 탐색을 예시로 보자.

x를 A 배열에서 찾는 과정이다. 루트에서 출발해서 비교를 통해서 x의 위치를 파악해낸다. x의 위치에 대한 모든 가능성이 나타나 있는 것을 볼 수 있다.
결정 트리와 알고리즘의 대응 관계는 다음과 같다.
| 결정 트리 | 알고리즘 |
|---|---|
| 내부 노드 | 비교 과정 |
| 잎(leaf) | 결과(알고리즘 완료) |
| 루트에서 잎까지의 경로 (root-to-leaf path) |
알고리즘 실행 |
| 경로 길이(깊이) | 실행 시간 |
| 트리의 높이 | 최악의 실행 시간 |
탐색 하한선 분석
탐색에 걸리는 시간의 하한선을 $\Omega(\log{n})$ 라고 했다. 이를 비교 모델로 유도해보자.
잎의 개수는 가능한 결과의 개수보다 많거나 같다. 그리고 이는 당연히 입력인 n(우리가 배열에서 찾고자 하는 것)보다 크거나 같다.
잎의 개수 $\geq$ 가능한 정답의 개수 $\geq$ n
결정 트리는 이진이고 모든 경우를 다 표현하기 때문에, 높이는 $\log{n}$ 보다 크거나 같다.
높이 $\geq \log{n}$
우리는 결정 트리의 높이가 곧 최악의 실행시간이라고 했다. 따라서 탐색에 걸리는 최소한의 시간은 $\Omega(\log{n})$ 이다.
정렬 하한선 분석
이번에는 정렬에 걸리는 하한선인 $\Omega(n\log{n})$ 도 분석해보자. 먼저 정렬에 사용되는 결정 트리의 특성에 대해 알아볼 필요가 있다. 결정 트리로 정렬을 하게 되면 마지막 단말 노드는 정렬된 배열 그 자체가 된다.
n개의 요소가 있는 배열에서 가능한 배열은 최대 몇 개일까? $n!$ 개 일 것이다. 즉, 잎의 개수는 $n!$ 보다 크거나 같다.
잎의 개수 $\geq n!$
이진트리이기 때문에 높이는 잎의 개수에 밑이 2인 로그를 취하면 된다.
높이 $\geq \log{n!}$
이제 우변을 조금 변형해보겠다.
\[\displaystyle 높이 \geq \log{n!} \\ = \log{1 \cdot 2 \cdots (n-1) \cdot n} \\ = \log{1} + \log{2} + \cdots + \log{(n-1)} + \log{n} \\ = \sum_{i=1}^{n}{\log{i}} \\ \geq \sum_{i=\frac{n}{2}}^{n}{\log{i}} \\ \geq \sum_{i=\frac{n}{2}}^{n}{\log{\frac{n}{2}}} \\ = \frac{n}{2} \log{n} - \frac{n}{2} = \Omega(n\log{n})\]정렬에 걸리는 최소 시간이 $\Omega(n\log{n})$ 임을 증명하였다.
선형 시간 정렬 - 계수 정렬
이제 선형의 시간이 걸리는 정렬에 대해 알아보자. n개의 키(key)가 ‘정수’일 때(0, …, k-1), 우리는 비교 말고도 다양한 연산을 할 수 있다. 여기서부터는 더 이상 하한선이 작동하지 않을 것이다. k가 너무 크지 않다면 우리는 정렬을 선형 시간 안에 할 수 있다.
선형 시간 안에 실행되는 정렬 중 하나는 계수 정렬(Counting Sort)이다. 파이썬 딕셔너리를 생각하면 쉽게 이해할 수 있다. 배열을 쭉 따라가면서 각 정수가 나타나는 횟수를 딕셔너리에 계속 업데이트하는 것이다. 배열을 다 따라갔다면 딕셔너리로 가서, 가장 작은 정수부터 나타나는 횟수만큼 적으면 된다.
예를 들어 53235라는 배열이 있다고 해보자. 배열을 따라가면 2가 한 번, 3이 두 번, 5가 두 번으로 딕셔너리에 기록될 것이다. 그럼 그냥 23355라고 쓰면 된다.
배열(파이썬 리스트)을 이용해서 표현할 수도 있다.
L = array of k empty lists
for j in range n:
L[key(A[j])].append(A[j])
output = []
for i in range k:
output.extend(L[i])
기본 아이디어는 딕셔너리와 동일하다. 다만 딕셔너리 대신 비어있는 리스트로 이루어진 배열 L을 사용한다고 보면 된다. 배열 L에서 A의 각 요소의 키에 해당하는 리스트로 이동해서(L[key(A[j])]), A[j] 를 추가하는 것이다.
시간을 얼마나 걸릴까? 가장 먼저 비어있는 리스트 L을 만드는 시간은 $O(k)$ 의 시간이 걸린다. 첫 번째 for문은 선형의 시간($O(n)$)이 걸리고, 두 번째 for 문은 (리스트가 비어있는지 확인 + 리스트 길이)를 i번 반복하므로 $\displaystyle O(\sum_{i}{(1 + \vert L[i] \vert)}) = O(k+n)$ 의 시간이 걸린다. 즉 최종적으로는 $O(k+n)$ 의 시간이 걸린다. k가 n과 비슷하다면 선형의 시간이겠지만, k가 엄청 크다면? 문제가 될 것이다.
선형 시간 정렬 - 기수 정렬
직전에 제기한 문제는 기수 정렬을 활용하면 해결된다. 기수 정렬은 k가 아무리 커도 선형의 시간을 유지한다. 기수 정렬(Radix Sort)은 쉽게 말하면 자릿수를 이용하는 정렬이다. 여기서 자릿수(d)는 $\log_{b}{k}$ 이다. 가장 낮은 자릿수의 숫자를 비교해서 정렬하고, 그 다음 자릿수를 비교해서 정렬하고, 그 다음 자릿수를 비교해서 다시 정렬하고, 이 과정을 반복한다.
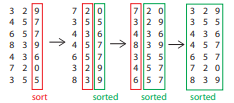
걸리는 시간을 계산해보자. 자릿수마다 정렬할 때 계수 정렬을 쓴다면 $\Theta(n+b)$ 의 시간이 걸린다(계수 정렬의 시간복잡도는 O(n+k),n은 데이터의 개수, k는 데이터들이 가질 수 있는 값의 수). 이것을 총 자릿수 k만큼 반복하므로 총 $\Theta((n+b) \log_{b}{k})$ 의 시간이 걸린다. b가 n과 동일할 때 이 값이 최소가 된다. 따라서 시간은 $\Theta(n \log_{n}{k}) = O(nc)$ 가 된다. 즉, 기수 정렬은 k의 값에 영향을 받지 않는 선형 시간 복잡도를 가진다.
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기