활주로 예약 시스템
활주로가 하나 뿐인 공항이 있다고 해보자. 비행기의 착륙이 동시에 이루어지면 매우 위험하기 때문에 우리는 활주로 예약 시스템을 만들어서 사고를 방지하고자 한다. 활주로 예약 시스템에 대한 규칙은 다음과 같다.
- 비행기가 착륙하면 대기 중인 집합에서 제거
- 각 착륙 요청에는 착륙 시각인 t가 있음.
- t로부터 k분 전이나 k분 후에 착륙이 없어야만 집합에 추가.
예시를 살펴보자. 아래와 같이 예약된 시스템에 몇 가지 착륙 요청을 추가하고자 한다.(k = 3)
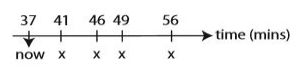
t = 53인 착륙 요청이 들어왔다. 시스템을 살펴보니 53을 기점으로 앞 뒤 3분씩이 비어있다. 착륙이 가능하다!
t = 44는 어떨까? 앞으로 3분은 비어있지만 뒤로 3분의 여유가 확보되지 않는다. 요청 반려다. 그 외에도 이미 지난 시간(t = 20) 등은 허용되지 않는다.
이제 우리의 목표는 이 시스템을 $O(\log{n})$ 시간 안에 효율적으로 운영하는 것이다. n은 집합 R의 사이즈($\vert R \vert$)이다.
예약 시스템의 여러 가지 후보
우리는 지금까지 많은 자료구조를 살펴보았다. 이 활주로 예약 시스템에 어떤 것이 어울릴지 생각해보자.
-
정렬된 리스트
(파이썬의 리스트가 아니다.) 리스트에서 추가 및 정렬에는 $O(n\log{n})$ 의 시간이 걸린다. 추가와 정렬을 하지 않고 삽입을 할 수도 있으나, 이진 탐색도 불가능해서 삽입에 $O(n)$ 의 시간이 걸린다. k분 떨어져 있는지 확인하는 데는 상수 시간이 걸리지만, 우리가 원하는 $O(\log{n})$ 시간 안에 해결하기는 글렀다. -
정렬된 배열
배열은 이진 탐색이 가능하다. 우리는 $O(\log{n})$ 시간 안에 삽입할 위치를 찾을 수 있다. 그런데 삽입하려고 보니, 배열에서 삽입을 하려면 이후 요소들을 모두 자리 이동 시켜야 한다. 자리 이동에는 $O(n)$ 의 시간이 걸린다. -
정렬되지 않은 리스트 및 배열
k분 떨어져 있는지 확인하는 데 $O(n)$ 의 시간이 걸린다. -
최소 힙
삽입은 $O(\log{n})$ 안에 가능하다. 근데 k분 떨어져 있는지는 어떻게 확인할 건가? 한 쪽 자식 노드 타고 넘어왔다고 다른 쪽 노드는 볼 필요가 없는 게 아니다. 결국 k분 조건 확인하는 데 $O(n)$ 의 시간이 걸린다. -
딕셔너리 및 파이썬 집합
k분 조건 확인하는 데 $O(n)$ 의 시간이 걸린다.
하나 같이 엉망이다(…) 우리는 다른 방법을 찾아야 한다.
이진 탐색 트리(BST)
이진 탐색 트리(Binary Search Tree, BST)는 활주로 예약 시스템에 딱 어울리는 자료구조이다.
BST의 각 노드 x에는 키인 key(x)가 있다. 루트가 아닌 다른 노드는 부모인 p(x)가 있다. 왼쪽 자식(left(x)), 오른쪽 자식(right(x))이 있으며, 힙과는 다르게 포인터이다.
BST의 불변성은 다음과 같다. 모든 노드 x와 x의 왼쪽 하위 트리에 있는 모든 노드 y에 대해 key(y) $\leq$ key(x) 이다. 쉽게 말해, 한 노드에 대해, 왼쪽 아래 노드의 키들은 모두 작다는 것이다. 마찬가지로 오른쪽 하위 트리의 모든 노드 y에 대해서는 key(y) $\geq$ key(x) </span>이다.
BST의 예시를 살펴보자. 먼저 49를 추가(insert(49))하고 싶다. 아무 것도 없는 상태이니 그냥 노드를 만들면 된다. 그 다음으로 79를 추가하고 싶다. 79는 49보다 크므로, 오른쪽 아래에 노드를 만든다.

다음으로 46을 추가하는데, 49보다 작으므로 왼쪽 아래에 노드를 만든다.

41은 어떨까? 49보다 작으니 왼쪽으로 내려온 뒤, 46보다도 작으니 또 왼쪽으로 내려온다.

아직 k분 조건을 확인하지는 않았다. 하지만 이는 간단한데, 그냥 대소비교를 할 때 k분 이내의 값인지 동시에 확인만 해주면 된다.
BST에서의 몇 가지 작업
BST에서는 다음과 같은 몇 가지 작업을 할 수 있다.
| 작업 | |
|---|---|
| insert(val) | val을 BST에 삽입 |
| find(val) | val을 BST에서 찾는다. 값을 찾거나 null에 도달할 때까지 트리를 타고 내려가면 된다. |
| findmin() | 최솟값 찾기. 트리의 왼쪽으로 계속 내려간다. |
| findmax() | 최댓값 찾기. 트리의 오른쪽으로 계속 내려간다. |
| next-larger(x) | x노드 다음으로 큰 값을 찾는다. |
위 모든 작업에 걸리는 시간은 $O(h)$ 이다. 여기서 h는 트리의 높이이다.
활주로 예약 시스템 - 새로운 조건 추가
우리의 프로그램 의뢰자들은 항상 새로운 기능을 추가하기를 원한다. 이번에는 t 시각 전에 착륙 예정인 비행기가 몇 대인지를 알 수 있는 Rank(t) 기능을 추가해달라고 요구했다.
이 문제를 우리가 가진 BST로 해결하기에는 너무 비효율적이다. 설령 t 값을 트리에서 찾는다고 하더라도 다시 루트로 이동해서 노드의 개수를 세어야 하기 때문이다.
BST 구조를 조금 보완한다면 효율적으로 해결할 수 있다. 먼저, 우리는 서브 노드의 개수를 트리에 추가적으로 적어줄 것이다. 다음과 같이 말이다.
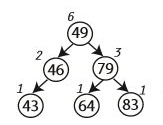
모든 단말 노드는 본인을 포함해서 서브 노드가 1개이므로 1을 적어주었다. 49의 경우 본인 포함 서브 노드가 6개이므로 6을 적었다.
Rank(t) 기능을 구현하기 위한 알고리즘은 다음과 같다.
- 원하는 시간 t를 찾기 위해 트리 탐색
- 1의 과정에서, 노드의 값이 찾는 값보다 작다면 1 더하기
- 2의 과정에서, 왼쪽 서브 트리의 노드 개수 더하기
위 BST를 이용해서 이해해보자. Rank(79)인 경우 어떻게 계산할까?
먼저 49 < 79 이므로 오른쪽으로 내려온다. 동시에 2에 의해 1을 더하고, 3에 의해 왼쪽 서브 트리의 노드 개수인 2를 더한다.
\[1(49) + 2 (subtree \, of \, 46)\]그리고 79와 비교한다. 작거나 같으므로 오른쪽으로 이동한다. 동시에 2에 의해 1을 더하고, 3에 의해 왼쪽 서브 트리의 노드 개수인 1을 더한다.
\[1(49) + 2 (subtree \, of \, 46) + 1(79) + 1 (subtree \, of \, 64)\]이제 모든 과정이 끝났다. Rank(79)는 5이다.
위 모든 과정은 $O(h)$ 의 시간에 해결된다.
여전히 풀리지 않는 의문
그럼 우리는 활주로 예약 시스템을 완전히 해결했을까? 다음 예시를 보자.
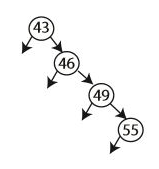
뭔가 이상하지 않은가? 분명 BST이다. 근데 리스트와 다를 바가 없다! 이 트리를 탐색하면 $O(\log{n})$ 가 아닌 $O(n)$ 의 시간이 걸린다. 지금까지 뭐 한거지?
다음 강의에서 배울 균형 BST가 이 문제를 해결할 수 있다.
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기