우선순위 큐
‘우선순위 큐(Priority Queue)’는 집합 S를 구현하는 자료 구조이다. 각 요소들은 우선순위를 뜻하는 키(key)를 가지고 있다. 우선순위 큐에서는 다음과 같은 작업들을 할 수 있다.
| 작업 | |
|---|---|
| insert(S, x) | 요소 x를 집합 S에 삽입 |
| max(S) | 최대 키인 S의 요소를 반환 |
| extract_max(S) | 최대 키인 S의 요소를 반환하고 집합 S에서 제거 |
| increase_key(S, x, k) | 요소 x의 키를 새로운 값 k로 증가시킴.(k가 현재 값만큼 크다고 가정) |
힙
힙은 우선순위 큐를 완전 이진 트리로 시각화한 것이다.
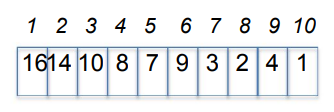

위와 같은 우선순위 큐를 아래와 같은 트리로 표현한 것을 힙이라고 한다. 각 노드들에 번호(인덱스)가 있으며 그에 맞는 키를 노드에 할당한다.
힙을 조금 더 엄밀하게 정의하면 다음과 같다.
- 트리의 루트(root): 배열의 첫 요소(i=1)
- parent(i) = i/2: 부모 노드의 인덱스는 자식의 절반
- left(i) = 2i: 왼쪽 자식 노드의 인덱스는 부모 인덱스의 두 배
- right(i) = 2i + 1: 오른쪽 자식 노드의 인덱스는 (부모 인덱스의 두 배 + 1)
최대 힙은 노드의 키가 자식 값들의 키보다 큰 것을 말한다. 위 힙을 살펴보면 자식 노드들의 키가 부모 노드보다 항상 작은 것을 볼 수 있다. 예를 들어 4번 노드를 보면, 2와 4는 8보다 작다.
힙의 높이는 $\log{n}$ 이다. 나중에 유용하게 사용될 특징이다.
힙에서는 다음과 같은 연산을 할 수 있다.
| 작업 | |
|---|---|
| build_max_heap | 정렬되지 않은 배열로부터 최대 힙 만들기 |
| max_heapify(힙, 인덱스) | 최대 힙화. 인덱스의 서브 트리에서 힙 특성을 위반한 것을 한 가지 고친다. |
max_heapity
말 그대로 최대 힙을 만족하도록 만드는 것을 최대 힙화(max heapify)라고 한다.
최대 힙화에는 몇 가지 가정과 전제 조건이 붙는다. 먼저, 왼쪽과 오른쪽 서브 트리들이 모두 최대 힙이라고 가정한다. 또한, 만약 요소 A[i]가 최대 힙 특성을 위반한다면, 요소 A[i]를 트리 아래로 보내면서(강의 노트에서는 ‘흘러 내려가도록’이라고 표현했다) i의 서브 트리들을 최대 힙으로 만든다.
최대 힙화의 예시를 살펴보자. 아래와 같은 힙이 있다.
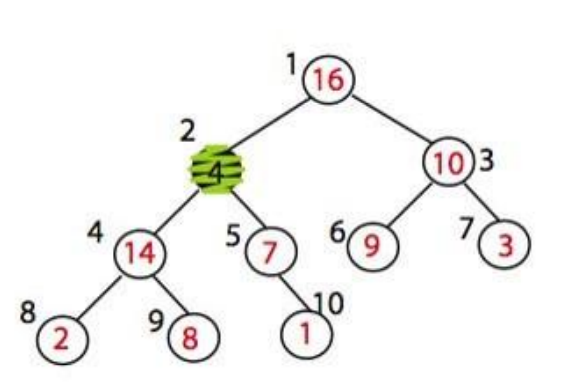
힙의 사이즈는 10이다(나중에는 힙의 크기도 중요하게 사용할 것이다).
max_heapify(A, 2)를 적용하면 어떻게 될까? A[2]와 A[4]를 교환할 것이다. 이제 A[2] 노드는 그 자체만으로는 최대 힙을 만족한다.
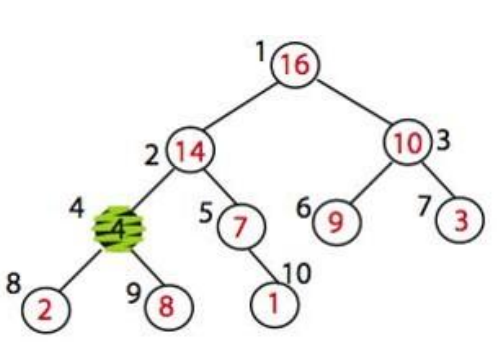
그러나 A[4]는 최대 힙을 위반하고 있다. 그래서 우리는 max_heapify(A, 4)를 할 것이다.
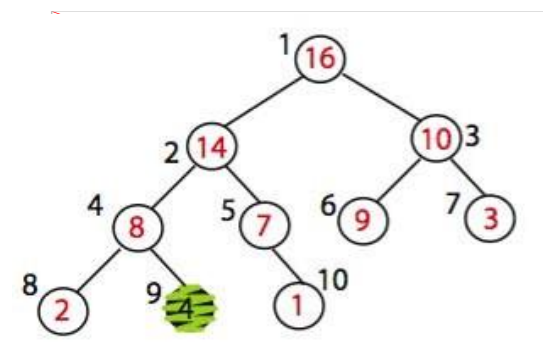
A[4]와 A[9]를 맞교환 했다. 이제 최대 힙 조건을 만족하는 힙이 되었다.
최대 힙화의 의사코드는 다음과 같다.
l = left(i) #왼쪽 자식의 인덱스
r = right(i) #오른쪽 자식의 인덱스
if l <= heap-size(A) and A[l] > A[i]:
largest = l
else:
largest = i
if r <= heap-size(A) and A[r] > A[largest]:
largest = r
if largest != i:
exchange A[i] and A[largest]
max_heapity(A, largest) #서브 트리로 계속 내려간다
최대 힙화의 시간은 어떻게 될까? 일단 힙은 완전 이진 트리로 높이가 $\log{n}$ 이다. 그리고 앞서 살펴본 전제 조건에 의해, 우리는 모든 노드를 살펴볼 필요 없이(만약 그랬다면 $O(n)$ 이었겠지만) 조건을 만족하지 않는 노드만 본다. 따라서 시간은 $O(\log{n})$ 이다.
build_max_heap
‘build_max_heap’은 A[1, …, n]을 최대 힙으로 변환하는 것이다. 다음과 같이 의사코드로 표현할 수 있다.
Build_max_heap(A):
for i = n/2 downto 1:
do max_heapify(A, i)
왜 n/2부터 시작할까? 트리 가장 아래에 있는 단말 노드들은 자식들이 없기 때문에 살펴볼 필요가 없기 때문이다.
build_max_heap은 시간이 얼마나 걸릴까? 간단하게 생각해보면 $O(n\log{n})$ 라고 할 수 있다. 그러나 이는 정확하지 않다! 그럼 정확하게 분석을 해보자.
먼저 단계에 따른 시간을 생각해본다. 단말 노드 바로 위에 있는 노드(1단계 노드)들에서는 max_heapify에 O(1)의 시간이 걸린다. 그럼 $l$단계 노드들은 어떨까? $O(l)$ 의 시간이 걸린다.
노드의 개수도 생각해볼까? 1단계에는 n/4 개의 노드, 2단계에서는 n/8 개의 노드, 점점 줄어들어 마지막에는 트리의 루트 1개만 남을 것이다.
전체 단계는 몇 단계인가? 앞서 보았듯이 $\log{n}$ 단계이다.
그럼 build_max_heap에서 하는 전체 일의 양은 다음과 같이 계산할 수 있을 것이다. (c는 상수)
\[n/4(1 \quad c) + n/8(2 \quad c) + n/16(3 \quad c) + ... + 1(\log{n} \quad c)\]n/4를 $2^k$ 라고 가정한다면 식이 다음과 같이 바뀐다.
\[c \; 2^k(1/2^0 + 2/2^1 + 3/2^2 + ... + (k+1)/2^k)\]괄호 안의 식은 결국 상수로 한정(수렴)된다. $2^k$를 다시 n/4로 바꾸어 보자. 결론적으로, build_max_heap의 복잡도는 O(n)이다.
build_max_heap의 예시를 살펴보자. 다음과 같은 힙이 있다.
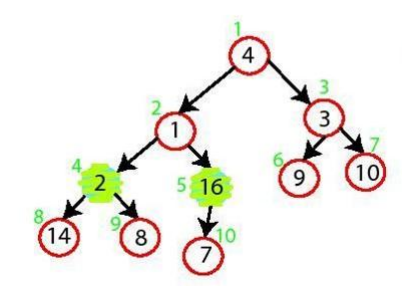
n/2부터 시작하므로, max_heapify(A, 5)를 할 것이다. 5번 노드를 보면 최대 힙을 잘 만족하므로 별 문제 없이 넘어간다.
다음으로 max_heapify(A, 4)를 한다. 최대 힙을 만족하지 않으므로, A[4]와 A[8]을 바꾼다.

다음으로 max_heapify(A, 3)를 한다. A[3]과 A[7]이 바뀌게 될 것이다.

max_heapify(A, 2)는 어떨까? 먼저 A[2]와 A[5]가 바뀐다. 그리고 A[5]와 A[10]도 바뀌게 될 것이다.
최종적으로 정리된 힙은 다음과 같다.

힙 정렬
힙을 이용하면 정렬을 쉽게 수행할 수 있다. 전략은 다음과 같다.
- 정렬된 배열에서 최대 힙을 만든다.
- 최대 요소 A[1]을 찾는다.
- 요소 A[n]와 A[1]을 스왑한다. 최대 요소가 배열 끝(단말 노드)으로 갈 것이다.
- 힙에서 노드 n을 제거한다.
- 새로운 루트는 최대 힙 특성을 위반할 것이므로, max_heapify로 해결한다.
- 힙이 비어있지 않다면 2단계로 돌아간다.
예시로 이해해보자.
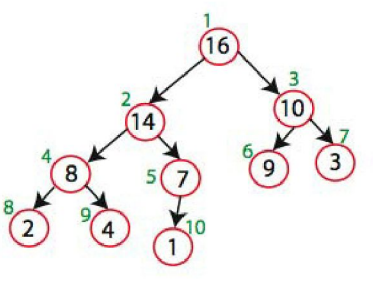
3번 단계에 따라 A[10]과 A[1]을 스왑한다. 그리고 4단계에 따라 노드 10을 제거한다.

최대 힙을 만족하지 않으므로 max_heapify(A, 1)을 한다. 그 다음에는 또 A[9]과 A[1]을 스왑하고 노드 9를 제거한다.

이를 계속 반복해서 최종적으로 힙이 비게 되면, 우리는 정렬된 배열을 얻게 된다.
힙 정렬의 실행 시간은 어떻게 될까? n번 반복한 후 힙이 비게 되며, 각 단계는 max_heapify를 포함하므로 $O(\log{n})$ 이 걸린다. 즉, 힙 정렬은 $O(n\log{n})$ 의 시간이 걸린다.
별도의 출처 표시가 있는 이미지를 제외한 모든 이미지는 강의자료에서 발췌하였음을 밝힙니다.

댓글남기기